
ПриклМех
.pdf
ра, а на расстоянии 3l – шарнирная подвижная опора. На стержень в плоскости xoz действуют внешние силы: q = 100 Н/м; Р = ql; М = ql2. Допускаемое напряжение материала стержня [σ] = 100 МПа.
Требуется: 1) построить эпюры поперечной силы Qz и изгибающего момента My; 2) определить положение опасного сечения и значения наибольших нормальных и касательных напряжений; 3) проверить прочность стержня; 4) определить напряжения в точке С (zc=h/4) сечения на площадке, составляющей угол α = 30° с осью х; 5) определить главные напряжения и положение главных площадок.
Решение. Обозначим реакции опор через А, H, B. Направления реакций выбираем произвольно. Запишем уравнения равновесия стержня:
|
|
Xi 0 |
|
H 0, |
|
|
i |
|
|
M ( y, A) 0 |
|
Pl M 1,5ql2 2Bl 0 B 0,75ql, |
||
i |
|
|
|
|
M ( y,B) 0 3Pl M 0,5ql2 2Al 0 A 1,25ql.
i
У стержня три грузовых участка. Проведем сечение на первом грузовом участке. Рассмотрим равновесие левой отсеченной части стержня (рис. 4.2):
Zi 0 |
P Qz 0 |
Qz P ql 20 Н, |
||
i |
|
|
|
|
M ( y,O1) 0 |
|
Px M y 0 |
M y Px qlx. |
|
|
|
Функция изменяется по линейному закону и |
||
|
принимает в граничных точках участка следую- |
|||
|
щие значения: M y (0) 0, |
M y (l) 4 Н м. |
||
Проведем сечение на втором грузовом участке. Рассмотрим равновесие левой отсеченной части стержня (рис. 4.3):
Zi 0 P A Qz 0 Qz A P 5 H; i
M ( y,O2 ) 0 |
Px A(x l) M y 0 |
M y Px A(x l). |
i |
|
|
21

Изгибающий момент изменяется по линейному закону и принимает в граничных точках участка следующие значения:
M y (l) 4 Н м, M y (2l) 0,75ql2 3 Н м.
Проведем сечение на третьем грузовом участке. Сечение делит стержень на две части. Рассмотрим равновесие правой отсеченной части (рис. 4.4):
Zi 0 |
B q(3l x) Qz 0, |
i |
|
|
Qz B q(3l x); |
M ( y,O3 ) 0 B(3l x) q(3l x)2 / 2 M y 0,
i
M y B(3l x) q(3l x)2 / 2.
На этом участке поперечная сила меняет знак, значит экстремальное значение изгибающего момента My в сечении, где Qz = 0:
dM y Qz 0 B q(3l x); x 2,25l M y (2,25l) 1,125 Н м. dx1
На рис. 4.5 построены эпюры поперечной силы Qz и изгибающего момента My. Следует отметить, что на эпюре My положительные значения принято откладывать вниз, отрицательные – вверх.
22

Опасным является сечение х = l, |
где M y |
M y |
max |
4 Н м (рис. 4.5). |
|
|
|
|
|
Определим наибольшие нормальные |
напряжения |
в опасном сечении: |
||
|
|
|
/ Wy 0, 278 105 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x max |
M y |
max |
Па. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Проверим |
прочность стержня: |
|
x max 0,278 105 Па 1 108 Па. |
||||||||||||||||||
Условие прочности выполняется. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Определим напряжения в точке С опас- |
||||||||||||||||
|
|
|
|
ного сечения (рис. 4.6): |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
x |
M yc |
zc 0,139 105 Па, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
J y |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Qz S*y |
|
|
20 |
|
bh 3h |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
xz |
|
|
|
4 8 |
|
0,313 104 |
Па. |
|||||||||
|
|
|
|
|
|
bz J y |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
bh3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Напряжения на площадке, составляющей угол 30 с осью х, определяем по формулам:
xcos2 xzsin 2 0,93 104 Па;2x sin 2 xzcos 2 0,76 104 Па.
Определим главные напряжения в точке С:
|
|
|
|
|
|
|
|
|
|
1,3 |
0,5 |
x |
2 |
2 |
0,65 кПа, |
3 14,5 кПа. |
|||
|
x |
4 xz . 1 |
|||||||
|
|
|
|
|
|
|
|
|
|
Положение главных площадок находим, используя формулу:
tg 2 |
2 xz |
1,625 |
|
2 58, 4 |
|
1 |
29, 2 , |
|
2 |
90 . |
|
||||||||||
|
x |
|
|
|
|
|
1 |
|||
|
|
|
|
|
|
|
|
|
||
Пример 5. На рис. 4.7 приведена стержневая расчетная схема элемента конструкции постоянного поперечного сечения высотой h и шириной b; h/b = 2. Стержень закреплен с помощью заделки. На стержень в плоскости xoz действуют внешние силы: q = 200 Н/м; Р = 100 Н; М = 50 Н ∙ м. Длина участка стержня l =1 м. Допускаемое напряжение для материала стержня
[σ]=200 МПа.
23

Требуется: 1) построить эпюры поперечной силы Qz и изгибающего момента My; 2) определить положение опасного сечения; 3) из условия прочности стержня определить размеры поперечного сечения b и h.
Решение. В заделке могут возникнуть реакции в виде горизонтальной и вертикальной сил и момента. Горизонтальная реакция в данном случае отсутствует, поскольку нет внешних сил, направленных вдоль оси x. Обозначим реакции в заделке через А и MA. Для нахождения опорных реакций запишем уравнения равновесия стержня:
Zi 0 A ql P 0 A 100 H, i
M ( y, A) 0 |
M A ql2 |
2 Pl M 0 |
M A 50 Н м. |
i |
|
|
|
У стержня два грузовых участка.
1. Первый грузовой участок: x (0, l) . Проведем сечение на этом участке. В сечении изобразим внутренние усилия Qz и M A , положительные в соответствии с правилом знаков. Рассмотрим равновесие левой отсеченной части стержня
(рис. 4.8):
Zi 0 A qx Qz =0 Qz A qx. i
Найдем значения перерезывающей силы на границах участка:
Qz (0) 100 Н, Qz (l) 100 Н.
Запишем уравнение равновесия для моментов относительно точки О1:
M ( y,O1) 0 M y M A qx2  2 Ax 0; M y M A qx2
2 Ax 0; M y M A qx2 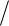 2 Ax.
2 Ax.
i
24
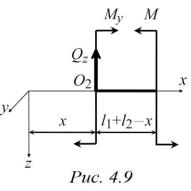
На границах участка M y (0) 50 Н м, M y (l) 50 Н м.
Найдем экстремум функции My (вершину параболы). Для этого приравняем нулю выражение для перерезывающей силы:
Qz A qxэ 0 xэ A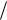 q 0,5 м,
q 0,5 м,
где xэ – координата, соответствующая экстремуму (принадлежит данному грузовому участку). Экстремальное значение изгибающего момента
M y (xэ ) 75 Н м.
Если xэ не принадлежит данному грузовому участку, то экстремума My нет, и для построения эпюры нужна третья точка. Для этого следует вычислить значение изгибающего момента для любого x (0, l) .
2. Второй грузовой участок: x (l, 2l). Проведем сечение на этом участке и отбросим левую часть. В сечении изобразим внутренние усилия Qz и M A , положительные в соответствии с правилом знаков (рис. 4.9). Рассмотрим равновесие пра-
вой отсеченной части стержня:
Zi 0 Qz 0; i
M ( y,O2 ) 0 M y M 0;
i
M y M 50 Н м.
Эпюры Qz и M A , построенные в соответствии с расчетами, показаны на рис. 4.10.
Определим положение опасного сечения. Опасным является сечение, в котором напряжение x максимально по модулю. Максимальному напряжению соответствует точка, где My = |My|max. Координата опасного сечения
х = 0,5 м, где My = |My|max = 75 Н · м (рис. 4.10).
25

Рассчитаем из условия прочности размеры сечения стержня. Запишем условие прочности при изгибе: M y max  Wи [ ] , где Wи – момент сопротив-
Wи [ ] , где Wи – момент сопротив-
ления сечения при кручении |
(W bh2 |
6 для |
прямоугольного сечения и |
|||||||||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(bh2 ) [ ]. С учетом |
||||
W r3 4 для круглого). В нашем случае 6 |
M |
y |
|
|
||||||||||
и |
|
|
|
|
|
|
|
|
|
|
max |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
условия h/b = 2 получим: b 3 |
3 |
|
M y |
|
max |
|
|
0,83 10 2 м, |
h 1,66 10 2 м . По- |
|||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||
|
|
2[ ] |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
лученные значения конструктор должен округлить до ближайших больших значений из ряда стандартных нормальных размеров (прил.2):
b = 0,85 см, h = 1,7 см.
Задание 3. На рис. 4.11 и в табл. 4.1 и 4.2 приведены расчетные схемы, геометрические параметры и внешние силовые факторы, вызывающие плоский поперечный изгиб в стержнях.
26

Требуется: 1) определить опорные реакции; 2) используя метод сечений, записать уравнения внутренних усилий Qz и My на каждом грузовом участке;
3)построить эпюры Qz и My; 4) определить положение опасного сечения;
4)подобрать для четных вариантов размеры круглого поперечного сечения стержня, а для нечетных вариантов – прямоугольного поперечного сечения, если h/b= 2. Материал стержня – Сталь 10.
|
|
|
|
|
|
|
Таблица 4.1 |
|
|
|
|
|
|
|
|
|
|
|
Вариант |
|
Длина участка, м |
|
Расчетная схема, |
|
||
|
l1 |
|
l2 |
|
l3 |
рис. 4.11 |
|
|
|
|
|
|
|
||||
|
1 |
0,4 |
|
0,1 |
|
0,3 |
а |
|
|
2 |
0,4 |
|
0,3 |
|
0,2 |
б |
|
|
3 |
0,3 |
|
0,2 |
|
0,1 |
а |
|
|
4 |
0,4 |
|
0,2 |
|
0,2 |
б |
|
|
5 |
0,3 |
|
0,2 |
|
0,3 |
а |
|
|
6 |
0,2 |
|
0,2 |
|
0,2 |
б |
|
|
7 |
0,1 |
|
0,3 |
|
0,1 |
а |
|
|
8 |
0,1 |
|
0,2 |
|
0,1 |
б |
|
|
9 |
0,2 |
|
0,2 |
|
0,3 |
а |
|
|
10 |
0,4 |
|
0,1 |
|
0,2 |
б |
|
|
11 |
0,1 |
|
0,2 |
|
0,2 |
а |
|
|
12 |
0,2 |
|
0,2 |
|
0,2 |
б |
|
|
13 |
0,3 |
|
0,1 |
|
0,2 |
а |
|
|
14 |
0,3 |
|
0,4 |
|
0,2 |
б |
|
27
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончание табл. 4.1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант |
|
|
|
Длина участка, м |
|
|
Расчетная схема, |
|
|
||||||||
|
|
l1 |
|
l2 |
|
|
l3 |
|
|
рис. 4.11 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
15 |
|
0,2 |
|
|
0,4 |
|
|
0,1 |
|
|
а |
|
|
|
|||
|
16 |
|
0,1 |
|
|
0,3 |
|
|
0,3 |
|
|
б |
|
|
|
|||
|
17 |
|
0,1 |
|
|
0,1 |
|
|
0,1 |
|
|
а |
|
|
|
|||
|
18 |
|
0,1 |
|
|
0,1 |
|
|
0,2 |
|
|
б |
|
|
|
|||
|
19 |
|
0,1 |
|
|
0,2 |
|
|
0,2 |
|
|
а |
|
|
|
|||
|
20 |
|
0,2 |
|
|
0,2 |
|
|
0,2 |
|
|
б |
|
|
|
|||
|
21 |
|
0,2 |
|
|
0,1 |
|
|
0,1 |
|
|
а |
|
|
|
|||
|
22 |
|
0,2 |
|
|
0,3 |
|
|
0,1 |
|
|
б |
|
|
|
|||
|
23 |
|
0,3 |
|
|
0,2 |
|
|
0,2 |
|
|
а |
|
|
|
|||
|
24 |
|
0,4 |
|
|
0,2 |
|
|
0,1 |
|
|
б |
|
|
|
|||
|
25 |
|
0,3 |
|
|
0,3 |
|
|
0,2 |
|
|
а |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Вари- |
Сосредоточенная |
Сосредоточенный |
Распределенная сила, |
|
|||||||||||||
|
|
|
сила, |
Н |
момент, Н·м |
|
|
Н/м |
|
|
|
|||||||
|
ант |
|
|
|
|
|
|
|
||||||||||
|
P1 |
|
P2 |
|
P3 |
M1 |
M2 |
M3 |
|
q1 |
q2 |
|
q3 |
|
||||
|
|
|
|
|
|
|
||||||||||||
|
1 |
–25 |
|
0 |
|
— |
6 |
0 |
4 |
0 |
150 |
|
200 |
|
|
|||
|
2 |
0 |
|
–70 |
|
–10 |
5 |
3 |
0 |
400 |
0 |
|
0 |
|
|
|||
|
3 |
30 |
|
50 |
|
— |
0 |
0 |
3 |
–100 |
0 |
|
200 |
|
|
|||
|
4 |
0 |
|
–40 |
|
0 |
|
4 |
0 |
1 |
0 |
100 |
|
100 |
|
|
||
|
5 |
–50 |
|
10 |
|
— |
0 |
0 |
–1 |
300 |
0 |
|
0 |
|
|
|||
|
6 |
60 |
|
0 |
|
–40 |
0 |
4 |
0 |
300 |
–300 |
|
0 |
|
|
|||
|
7 |
20 |
|
–50 |
|
— |
–7 |
0 |
2 |
0 |
0 |
|
400 |
|
|
|||
|
8 |
20 |
|
0 |
|
–30 |
0 |
2 |
6 |
0 |
0 |
|
150 |
|
|
|||
|
9 |
0 |
|
–60 |
|
— |
0 |
0 |
–3 |
100 |
–100 |
|
100 |
|
|
|||
|
10 |
30 |
|
–30 |
|
30 |
|
5 |
0 |
0 |
100 |
120 |
|
0 |
|
|
||
|
11 |
40 |
|
–30 |
|
— |
0 |
–6 |
0 |
50 |
0 |
|
0 |
|
|
|||
|
12 |
–30 |
|
0 |
|
0 |
|
0 |
0 |
1,5 |
140 |
–90 |
|
0 |
|
|
||
|
13 |
50 |
|
0 |
|
— |
0 |
–2 |
0 |
0 |
100 |
|
–80 |
|
||||
|
14 |
20 |
|
–20 |
|
0 |
|
0 |
0 |
3 |
–200 |
300 |
|
0 |
|
|
||
|
15 |
0 |
|
40 |
|
— |
0 |
0 |
4 |
–300 |
0 |
|
200 |
|
|
|||
|
16 |
–40 |
|
0 |
|
–10 |
2 |
0 |
.0 |
200 |
0 |
|
160 |
|
|
|||
|
17 |
0 |
|
20 |
|
— |
0 |
–3 |
0 |
0 |
–130 |
|
–120 |
|
||||
|
18 |
0 |
|
0 |
|
10 |
|
3 |
0 |
0 |
0 |
0 |
|
–110 |
|
|||
|
19 |
30 |
|
20 |
|
— |
0 |
–2 |
0 |
0 |
–300 |
|
60 |
|
|
|||
|
20 |
0 |
|
20 |
|
10 |
|
0 |
–5 |
2 |
100 |
0 |
|
0 |
|
|
||
|
21 |
20 |
|
10 |
|
— |
4 |
2 |
0 |
–200 |
0 |
|
0 |
|
|
|||
|
22 |
–10 |
|
40 |
|
0 |
|
0 |
–5 |
4 |
300 |
0 |
|
–100 |
|
|||
|
23 |
0 |
|
–50 |
|
— |
5 |
0 |
0 |
0 |
150 |
|
100 |
|
|
|||
|
24 |
40 |
|
0 |
|
–30 |
0 |
2 |
5 |
0 |
300 |
|
0 |
|
|
|||
|
25 |
30 |
|
20 |
|
— |
0 |
4 |
0 |
0 |
200 |
|
–200 |
|
||||
28
Приложение 1. Механические характеристики конструкционных материалов
В таблице приняты следующие обозначения: ρ – плотность материала;
α – температурный коэффициент линейного расширения материа-
ла;
σт – предел текучести материала; [σ] – предельно допустимое нормальное напряжение;
σв+ – временное сопротивление материала при растяжении; σв– – временное сопротивление материала при сжатии; Е – модуль нормальной упругости (модуль Юнга) материала; ν – коэффициент Пуассона.
|
|
|
|
|
|
|
|
Таблица |
||
|
|
|
|
|
|
|
|
|
|
|
№ |
Материал |
ρ, |
α·106, |
σт, |
[σ], |
σв+, |
σв–, |
Е·10–5, |
ν |
|
г/см3 |
К–1 |
МПа |
МПа |
МПа |
МПа |
МПа |
||||
|
|
|
||||||||
1 |
Медь М1, М2, М3 |
8,96 |
16,5 |
380 |
100 |
400 |
– |
1,2 |
0,35 |
|
2 |
Ковар 29 НК |
8,35 |
4,7…5,2 |
350 |
200 |
600 |
– |
1,42 |
0,32 |
|
3 |
Никель НП-2 |
8,9 |
13 |
590… |
– |
630… |
– |
2,1 |
0,3 |
|
740 |
770 |
|||||||||
|
|
|
|
|
|
|
|
|||
4 |
Сталь 10 |
7,86 |
11,9 |
250 |
130 |
400 |
– |
2,1 |
0,28 |
|
5 |
Сталь СТ5 |
7,8 |
12,5 |
290 |
120 |
– |
– |
2,1 |
0,27 |
|
6 |
ЗИ-693 |
8,1 |
12 |
500 |
– |
– |
– |
2 |
0,3 |
|
7 |
47НД |
3 |
9,5 |
500 |
– |
– |
– |
2 |
0,3 |
|
8 |
Латунь Л68, |
8,4 |
18 |
160 |
– |
400 |
– |
0,9 |
0,4 |
|
ДС59-1 |
||||||||||
|
|
|
|
|
|
|
|
|
||
9 |
Молибден МО |
10,2 |
5,5 |
590 |
300 |
1400 |
– |
3,2 |
0,31 |
|
10 |
Вольфрам |
19,1 |
4,4 |
400… |
– |
800 |
– |
4 |
0,17 |
|
560 |
||||||||||
|
|
|
|
|
|
|
|
|
||
11 |
Золото |
19,3 |
14,4 |
– |
– |
122 |
– |
0,84 |
0,38 |
|
12 |
Серебро |
10,5 |
18,9 |
– |
– |
138 |
– |
0,77 |
0,49 |
|
13 |
Платина |
21,45 |
7,8 |
– |
– |
143 |
– |
1,47 |
0,21 |
|
14 |
Свинец |
11,36 |
28,9 |
50… |
– |
150… |
– |
0,18 |
– |
|
100 |
180 |
|||||||||
|
|
|
|
|
|
|
|
|||
15 |
Алюминий АЛ2 |
2,7 |
23,8 |
100 |
– |
200 |
– |
0,7 |
0,33 |
|
16 |
Псевдосплав |
9 |
7 |
500 |
– |
– |
– |
1,9 |
0,3 |
|
17 |
Ситалл АС-336 |
2,5 |
3 |
– |
– |
– |
690 |
0,67 |
0,25 |
|
18 |
Ситалл СТ |
7,49 |
7,6 |
– |
– |
– |
630 |
0,77 |
0,3 |
|
19 |
Кремний |
2,33 |
2,5…4,1 |
– |
– |
24 |
62 |
1,13 |
0,3 |
|
20 |
Германий GE |
5,33 |
5,75 |
– |
– |
– |
– |
– |
– |
|
29
Окончание таблицы
№ |
Материал |
ρ, |
α·106, |
|
σт, |
[σ], |
σв+, |
σв–, |
Е·10–5, |
ν |
г/см3 |
К–1 |
|
МПа |
МПа |
МПа |
МПа |
МПа |
|||
|
|
|
|
|||||||
|
|
|
Керамика |
|
|
|
|
|
||
1 |
Алюмоксид 22ХС |
3,6 |
6,1 |
|
– |
– |
130 |
1100 |
2,2 |
0,25 |
2 |
М7 |
3,65 |
7,9 |
|
– |
– |
83 |
600 |
2,04 |
0,22 |
3 |
Берилливая Вео |
2,85 |
5,3…8,9 |
|
– |
– |
100 |
800 |
2,4 |
0,2 |
4 |
Поликор |
3,96 |
7,8 |
|
– |
– |
250 |
– |
3,92 |
3,92 |
5 |
А-995 |
3,5 |
7,5 |
|
– |
– |
100 |
980 |
3,8 |
3,8 |
|
|
|
Стекло |
|
|
|
|
|
||
1 |
Кварцевое |
2,21 |
0,4…0,6 |
|
– |
– |
40 |
500 |
0,75 |
0,26 |
2 |
Молибденовое |
– |
4,1 |
|
– |
– |
60 |
600 |
0,5 |
0,25 |
3 |
Электровакуумное |
– |
5,2 |
|
– |
– |
– |
– |
0,66 |
0,22 |
4 |
С48-1 |
2,1 |
4,85 |
|
– |
– |
77 |
700 |
0,58 |
0,3 |
5 |
С48-2 |
2,3 |
4,8 |
|
– |
– |
20 |
300 |
0,58 |
0,29 |
6 |
С49-1 |
2,29 |
4,7 |
|
– |
– |
40 |
400 |
0,58 |
0,28 |
|
|
|
|
Припой |
|
|
|
|
|
|
1 |
Оксид олова |
7,3 |
23,4 |
|
11.7 |
– |
16 |
– |
0,42 |
0,3 |
2 |
ПОИ и КС |
8,2 |
29,7 |
|
– |
30 |
23,9 |
– |
0,3 |
0,29 |
3 |
ПОС-61 |
8,1 |
19 |
|
– |
30… |
43 |
– |
0,35 |
0,29 |
|
40 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
ПСР-72 |
10 |
16,1 |
|
– |
60 |
46 |
– |
0,3 |
0,3 |
30
