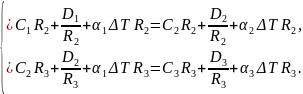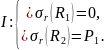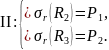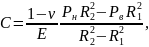ИДЗ№2топ

МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра прикладной механики и инженерной графики

ОТЧЁТ по индивидуальному домашнему заданию №2 по дисциплине «Прикладная механика» Тема: Анализ температурных напряжений Вариант №1-2

Студентка гр. 1283 ____________________ Григорьева В.В. Преподаватель __________________________ Титов А.В.

Санкт-Петербург 2024

1. ИСХОДНЫЕ ДАННЫЕ

Общий вид прибора представлен на рисунке 1. Исходные данные для расчёта приведены в таблицах 1 – 2. Расчет температурных напряжений необходимо провести для деталей 1, 2, 3 в сечениях их контакта.

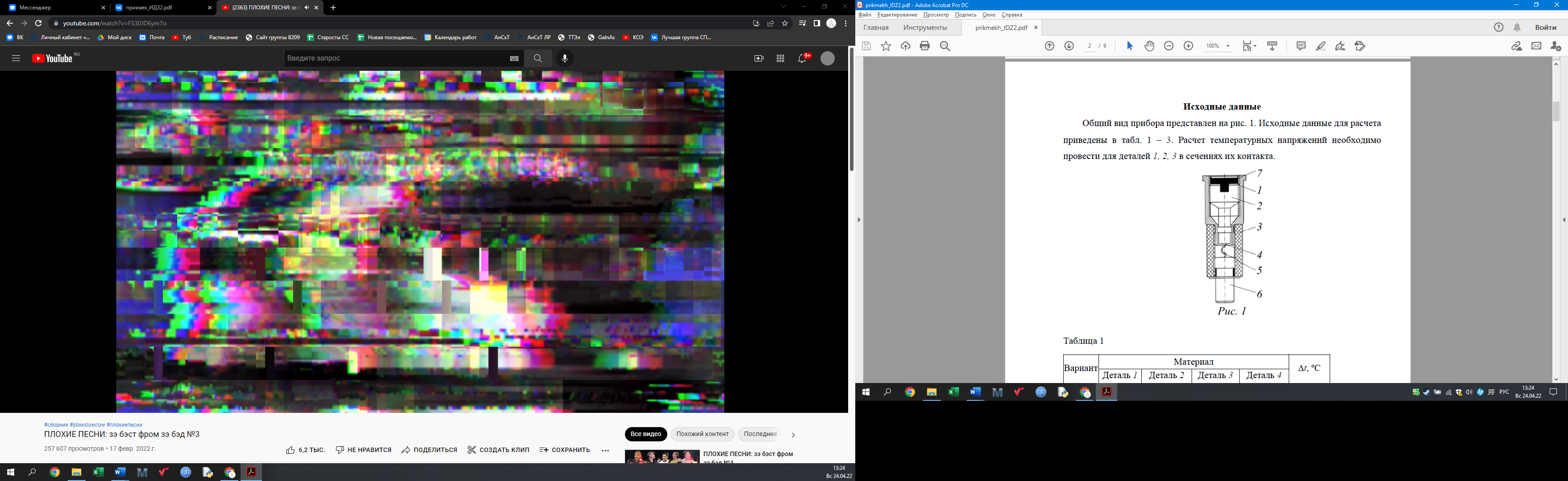
Рисунок 1 – Общий вид прибора

Таблица 1 – Исходные данные для расчёта
Вариант	Материал				t, ºС
	Деталь 1	Деталь 2	Деталь 3	Деталь 4
1-2	Латунь	Латунь	ВеО	Латунь	220

Таблица 2 – Параметры первой детали, необходимые для расчётов
Вариант	d1нар, мм	d2нар, мм	d3нар, мм	l1, мм	l2, мм	l3, мм	d1вн, мм	d2вн, мм
1-2	7,0	6,0	М3	0,8	3,8	1,8	М4	1,3

Таблица 3 – Параметры второй детали, необходимые для расчётов
Вариант	d, мм	l1, мм	l2, мм	l3, мм	l4, мм
1-2	1,0	1,8	1,8	0,5	1,2

Таблица 4 – Параметры третьей детали, необходимые для расчётов
Вариант	dнар, мм	l1, мм
1-2	4,0	6,0

Таблица 5 – Параметры четвёртой детали, необходимые для расчётов
Вариант	d1, мм	d2, мм	l1, мм	l2, мм	l3, мм	l4, мм
1-2	3,8	1,8	1,0	0,7	0,2	2,2

Таблица 6 – Механические характеристики конструкционных материалов

№	Материал	ρ, г/см3	α·106, К–1	σт, МПа	[σ], МПа	σв+, МПа	σв–, МПа	Е·10–5, МПа	ν
1	Латунь Л68, ДС59-1	8,4	18	160	–	400	–	0,9	0,4
2	Оксид бериллия	2,85	5,3…8,9	–	–	100	800	2,4	0,2

2. РАСЧЁТНАЯ ЧАСТЬ

1. Представили корпус прибора в виде трёхслойного цилиндра. Для нахождения температурных напряжений построили расчётную схему на рисунке 2, представляющую собой сечение, где три детали находятся в контакте:

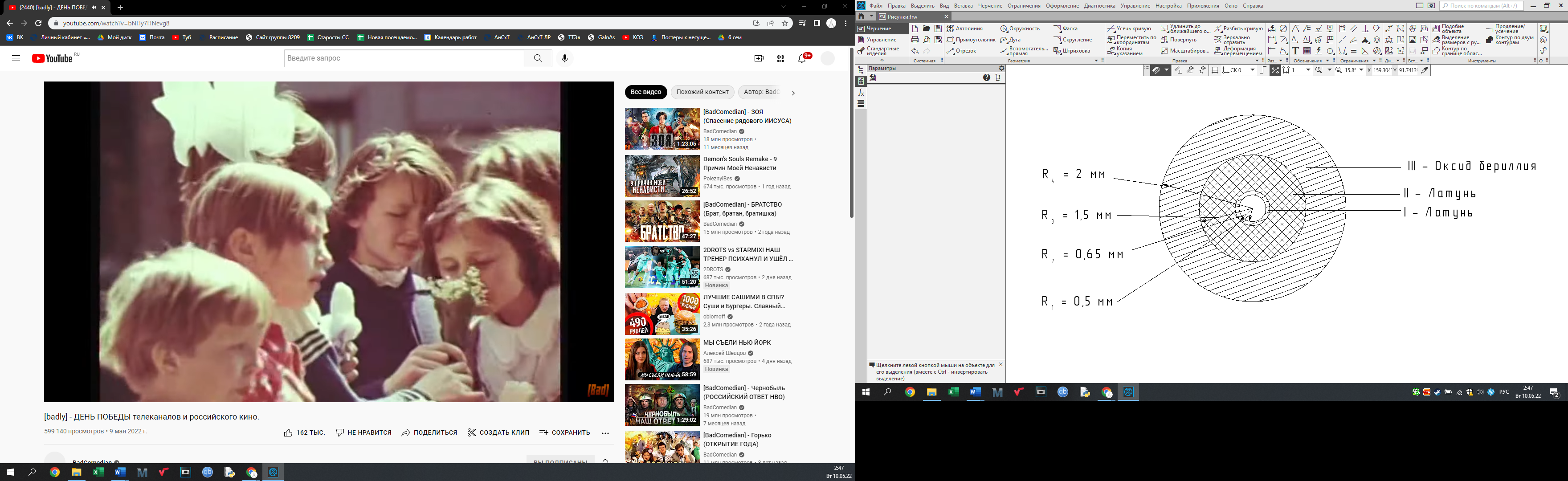
Рисунок 2 – Расчётная схема для трёхслойного цилиндра

Записали уравнения совместности перемещений (1):

(1)

где σ_i – нормальные напряжения i-ой детали (i = 1,2,3),

R_i – радиус контактной поверхности цилиндра.

Переписали их, учитывая, что перемещение осуществляется за счёт температурного и механического воздействий и подставляя радиусы (2):

(2)

где C_i и D_i – произвольные постоянные i-ой детали,

α_i – температурный коэффициент линейного i-ой детали,

ΔT – разница между конечной и начальной температурами нагрева конструкции.

Также записали граничные условия (3) для трех цилиндров:

(3)

где Р_i –давления, возникающие между соответствующими цилиндрами.

Уравнения на коэффициенты С и D в общем виде (4):

(4)

где υ – коэффициент Пуассона,

Е – это модуль нормальной упругости материала, из которого изготовлен цилиндр,

P_н, P_в – наружное и внутреннее давление.

Записали эти уравнения для каждого цилиндра:

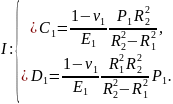
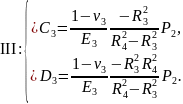
Подставили известные значения:

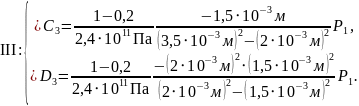
Получили следующие выражения:

Подставили в (2), разделили на радиусы и получили систему уравнений для нахождения P₁ и P₂:

Решив систему, получили:

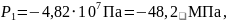
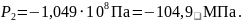
Отсюда получили значения коэффициентов С_i и D_i:

Для расчёта внутренних напряжений в каждом цилиндре применили следующие функции (5):

(5)

Расчётные значения привели в таблице 4:

Таблица 4 – Расчётные значения напряжений

Цилиндр	r, мм
1	0,50	0,000	-236,1042857
	0,55	-20,484	-215,6155254
	0,60	-36,068	-200,0321429
	0,65	-48,195	-187,9046069
2	0,65	-48,195	-187,905
	0,70	-57,818	-178,282
	0,80	-71,935	-164,165
	0,90	-81,613	-154,487
	1,00	-88,536	-147,564
	1,10	-93,659	-142,441
	1,20	-97,554	-138,546
	1,30	-100,586	-135,514
	1,40	-102,992	-133,108
	1,50	-104,933	-131,167
3	1,50	-104,912	374,732
	1,55	-89,689	359,509
	1,60	-75,871	345,691
	1,65	-63,290	333,110
	1,70	-51,803	321,623
	1,75	-41,286	311,106
	1,80	-31,633	301,453
	1,85	-22,753	292,573
	1,90	-14,564	284,384
	1,95	-6,997	276,817
	2,00	0,000	269,810

Построили эпюры напряжений – радиального на рисунке 3, углового – на рисунке 4:

Рисунок 3 – Эпюра радиального напряжения

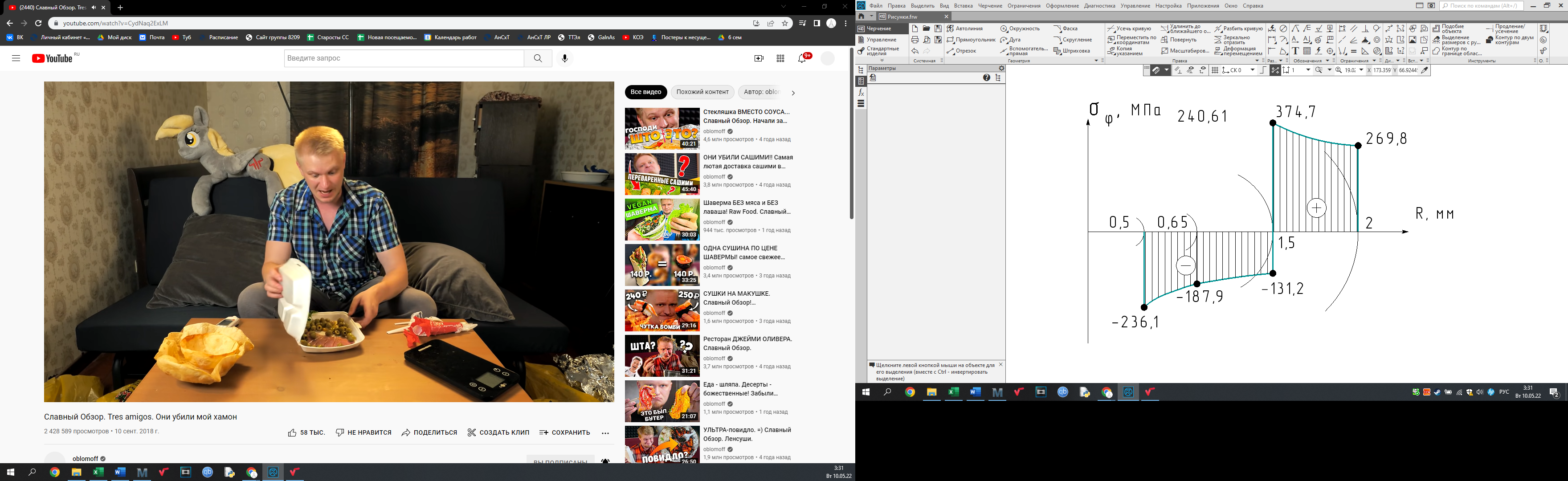
Рисунок 4 – Эпюра углового напряжения

2. Анализ прочности для каждого цилиндра:

1. I цилиндр. Латунь – пластичный материал, поэтому можно использовать третью теорию прочности. Выбрали максимальное по модулю напряжение – при r = 0,5 мм σ₁ = σ_r = 0, а σ₃ = σ_φ = – 236,1 МПа. Тогда получили:

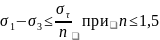
Таким образом, так как n_расч = 0,678 < 1,5 = n_теор сделали вывод о том, что условие прочности не выполняется.

2. II цилиндр. Латунь – пластичный материал, поэтому можно использовать третью теорию прочности. Выбрали максимальное по модулю напряжение – при r = 0,65 мм σ₁ = σ_r = – 48,2 МПа, σ₂ = 0 МПа, а σ₃ = σ_φ = – 187,9 МПа. Тогда получили:

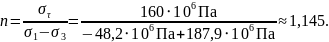
Таким образом, так как n_расч = 1,145 < 1,5 = n_теор сделали вывод о том, что условие прочности не выполняется.

3. III цилиндр. Оксид бериллия – хрупкий материал, поэтому нужно использовать вторую теорию прочности. Выбрали максимальное по модулю напряжение – при r = 1,5 мм σ₁ = σ_r = – 104,9 МПа, а σ₃ = σ_φ = 374,7 МПа. Тогда получили:

Таким образом, так как n_расч = 0,392 < 1,5 = n_теор сделали вывод о том, что условие прочности не выполняется.