МАТАН ЭКЗАМЕН / 22 / формула лейбница

Пусть y = u·v, где u и v — некоторые функции от переменной x, имеющие производные любого порядка. Тогда

.

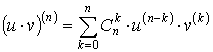где  есть число сочетаний из n элементов по k (k = 0, 1, 2, …, n). Доказательство. Для k = 1 имеем

для k = 2 имеем

для k = 3 имеем

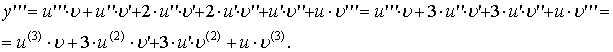
Правые части полученных равенств похожи на разложения различных степеней бинома (u + v)ⁿ по формуле Ньютона, но вместо показателей степени стоят числа, определяющие порядок производных, а сами функции u и v для полной аналогии с формулой Ньютона нужно рассматривать как «производные нулевого порядка»: u⁽⁰⁾ и v⁽⁰⁾.    Пусть формула Лейбница справедлива при k = n:

.

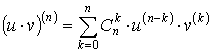Докажем, что формула справедлива при k = n + 1. Действительно, в этом случае

Здесь воспользовались свойством сочетаний . Изменим индекс суммирования во второй сумме, положив k = p- 1. В этом случае

и в полученных суммах объединим попарно слагаемые, содержащие производные одинаковых порядков. После обозначения общего индекса суммирования через р, будем иметь

.

Так как  и , получим

.

   Пример 3. Вычислить n - ю производную (n ≥ 2) функции y = x²·cos x.    Решение. В этом случае u = cos x  и v = x² и

Подставляя в формулу Лейбница, получаем