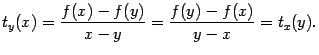МАТАН ЭКЗАМЕН / 40 / условие выпуклости графиков функции

 Выпуклость функции

        Определение 7.5   Функция  называется выпуклой вниз (или просто выпуклой) на интервале , если график функции  идёт не выше хорды, соединяющей любые две точки графика  и  при .

Пусть . Тогда любую точку отрезка  можно задать как , , а любую точку хорды -- как . Выражение  задаёт линейную функцию переменного , график которой на отрезке  совпадает с хордой.

То, что график функции идёт не выше хорды, означает, что

(7.4)

при всех .

Аналогично определяется выпуклость вверх: функция  называется выпуклой вверх (или вогнутой) на интервале , если график функции  идёт не ниже хорды, соединяющей любые две точки графика  и  при . Это означает, что

(7.5)

при всех .     

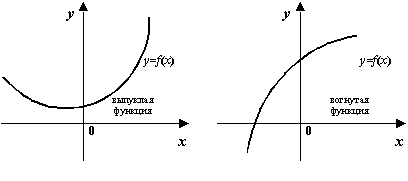
Рис.7.30.Графики выпуклой и вогнутой функций

Легко видеть, что функция  вогнута на интервале  в том и только том случае, когда функция  выпукла на .

        Пример 7.28   Рассмотрим функцию . Эта функция выпукла на любом интервале оси . Действительно, если интервал не содержит точки 0, то графики  и  на таком интервале совпадают, откуда следует, что неравенство (7.4) выполнено и функция выпукла. (Заметим, что на таком интервале верно и неравенство (7.5), так что  одновременно и выпукла, и вогнута на таком интервале.) Если же точка 0 лежит в интервале , то  и , и тот факт, что хорда лежит выше графика, геометрически очевиден.     

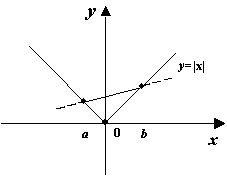
Рис.7.31.Хорда лежит выше графика 

        Пример 7.29   Рассмотрим функцию ; её график -- парабола . 

Рис.7.32.Функция  -- выпуклая

Мы привыкли изображать параболу именно так, что очевидно: хорда идёт выше графика на любом интервале . Подтвердим теперь это свойство формальной выкладкой. Имеем:

Здесь мы использовали известное неравенство:  при всех .¹⁸     

        Теорема 7.9   Пусть функция  определена на интервале  и  -- некоторая точка этого интервала. При всех  определено разностное отношение -- функция

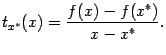
Тогда функция  выпукла на интервале  в том и только том случае, когда функция  не убывает на множестве .

        Замечание 7.7   Функция  равна тангенсу угла наклона хорды, одним из концов которой служит фиксированная точка , а вторым концом -- переменная точка графика . Тем самым, теорема означает, что у выпуклых функций угловые коэффициенты хорд графика не убывают, где бы ни был фиксирован один из концов хорды. 

Рис.7.33.Угловой коэффициент хорды с фиксированным концом возрастает, если функция выпукла

Заметим также, что функция  имеет следующее свойство:

(7.6)

Действительно,

    

        Доказательство теоремы 7.9.     Выберем любые две точки . Предположим, что  (случаи иного расположения точек  рассматриваются аналогично). Поскольку , то  при некотором . Нетрудно видеть, что тогда  и . Поэтому из выпуклости функции  следует, что

Умножая на , получаем:

Теперь вычтем  из обеих частей неравенства. Получим, после раскрытия скобок в правой части и приведения подобных членов:

Теперь разделим обе части неравенства на  и  и получим:

то есть

Это означает, что функция  -- неубывающая.

Доказательство того, что из неубывания функции  следует выпуклость функции , можно провести, если проделать все преобразования в обратном порядке.      

        Замечание 7.8   Очевидно, что аналогично доказывается следующее утверждение:

функция  вогнута на интервале  тогда и только тогда, когда при любом  функция  не возрастает на множестве .     

Доказанная теорема содержит хотя и важный, но всё же вспомогательный результат. На её основании мы получим следующее утверждение, которое уже гораздо удобнее применять на практике для исследования выпуклости.

        Теорема 7.10   Пусть функция  имеет на  производную . Функция  выпукла на  тогда и только тогда, когда производная  не убывает на .

        Доказательство.     Пусть  -- выпуклая функция. Возьмём точки  на интервале  так, чтобы они следовали в таком порядке: . По предыдущей теореме, функции  и  не убывают. Пользуясь также свойством (7.6), получаем цепочку:

В итоге получили, что , или

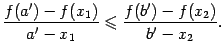
Перейдем в левой части к пределу при , а затем в правой части при . Так как, по предположению, производная в точках  и  существует, то односторонние пределы существуют и равны производным в соответствующих точках, то есть . Ввиду того, что точки  и  можно было выбирать произвольно, это означает, что  не убывает на .

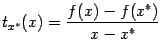Пусть теперь производная  -- неубывающая функция. Фиксируем точку  и найдём производную функции  при . Она равна

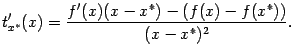
По формуле конечных приращений мы можем представить  в виде

где  -- некоторая точка, лежащая между  и . Заметим, что при этом знак разности  -- тот же, что у разности . Получаем, что

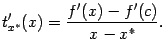
Так как  -- неубывающая функция, то  при  и, следовательно, при  и  при  и, следовательно, при . В любом случае отношение неотрицательно, то есть . По теореме 7.2 отсюда следует, что функция  не убывает, а по теореме 7.9 -- что функция  выпукла.      

        Замечание 7.9   Разумеется, верно следующее утверждение, аналогичное доказанной теореме:

дифференцируемая функция  вогнута на интервале  тогда и только тогда, когда её производная  не возрастает.     

Если функция имеет во всех точках интервала вторую производную , то для исследования выпуклости можно воспользоваться следующим утверждением, которое вытекает из доказанной теоремы.

        Теорема 7.11   Пусть на интервале  функция  имеет вторую производную . Функция  выпукла на  тогда и только тогда, когда  при всех , и вогнута тогда и только тогда, когда  при всех .

        Доказательство.     Производная  не убывает на  в том и только том случае, когда  при всех , и не возрастает в на  в том и только том случае, когда  при всех . Поэтому утверждение теоремы сразу следует из теоремы 7.10 и замечания 7.9.      

Именно эту теорему чаще всего применяют для исследования выпуклости и вогнутости функции на заданном интервале, а также для нахождения интервалов выпуклости и интервалов вогнутости данной функции. 

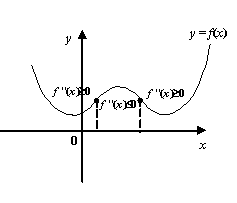
Рис.7.34.  на интервалах выпуклости и  на интервалах вогнутости

        Пример 7.30   Рассмотрим функцию , то есть

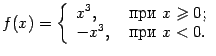
Для этой функции

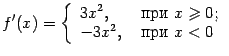
(проверьте отдельно, что производная при  существует и равна 0) и

то есть . (Также проверьте, что производная в точке 0 существует и равна 0.) Итак,  при всех ; отсюда следует, что функция  выпукла на всей оси.     

Рис.7.35.Функция  выпукла на всей оси

        Пример 7.31   Рассмотрим функцию примера 7.24: . Её производная равна ; вторая производная . Чтобы найти интервалы выпуклости, решим неравенство , то есть . Решением является объединение лучей: 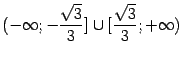. Значит, на интервалах 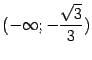 и  функция выпукла.

Для нахождения интервала вогнутости нужно решить неравенство , то есть . Решением является отрезок . Значит, на интервале  функция вогнута.     

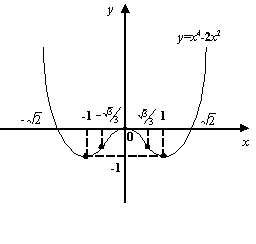
Рис.7.36.Интервалы выпуклости и вогнутости функции 

Выпуклые функции обладают следующим весьма важным свойством: они могут иметь не более одного локального минимума на интервале выпуклости. А именно, верна следующая теорема.

        Теорема 7.12   Пусть  -- выпуклая на  функция и  -- точка локального минимума функции . Тогда 

        Замечание 7.10   Теорема не означает, что функция не может иметь много точек локального минимума, однако утверждает, что во всех таких точках выпуклая функция принимает одно и то же значение      

        Доказательство теоремы.     Пусть  и  -- две различные точки локального минимума функции , причём  и  (случай  разбирается аналогично). Положим  и рассмотрим линейную функцию , на графике которой лежит хорда, соединяющая точки  и . Так как функция выпукла, то  при всех , то есть при всех . Это неравенство верно, в том числе, и при любом  из некоторой правой окрестности точки , то есть при , . Тем самым получаем для таких :

Однако это противоречит тому, что  -- точка локального минимума (из того, что  -- точка локального минимума, следует, что при достаточно малом  при  имеет место неравенство ).

Значит, предположение о том, что , не может быть верным. Точно так же доказывается, что неверно и предположение о том, что . Следовательно, , то есть во всех точках локального экстремума (если их не одна) функция  принимает одно и то же значение.      

Тем самым, если о функции  известно, что она выпукла, и мы нашли некоторую точку локального минимума , то значение в этой точке -- это минимальное значение функции на всём рассматриваемом интервале: . Если нас интересует лишь это минимальное значение, а не полный набор точек минимума, то мы можем других точек локального минимума не искать.

        Замечание 7.11   Свойство, аналогичное доказанной теореме, верно и для максимумов вогнутых функций:

если  -- вогнутая функция на интервале  и  -- точки локального максимума, то