МАТАН ЭКЗАМЕН / 25 / извлечение корней из комплексных чисел
.docxИзвлечение корня из комплексного числа
Пусть 
означает
натуральное число. Корнем 
-й
степени из
комплексного числа 
называется
такое комплексное число 
,
что 
.
Очевидно, что корень первой степени
из 
совпадает
с самим числом 
и
корень любой степени из 
равен 
(в
дальнейшем эти случаи рассматривать
не будем). Обозначение корня при 
такое
же как и в случае вещественных чисел:
а
при 
показатель
обычно не указывают: 
Задача. Вычислить 
.
Квадратный корень
Пусть 
представлено
в каноническом виде: 
при 
.
Будем искать число 
также
в каноническом виде: 
,
где 
и 
неизвестные вещественные величины.
По определению квадратного корня, должно
быть выполнено:
(на основании аксиомы равенства комплексных чисел). Возведем оба получившихся уравнения в квадрат и сложим:
(поскольку 
)
Вместе
с первым уравнением получаем линейную
систему относительно 
и 
.
Решаем ее относительно 
:
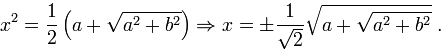
Имеем: 
.
В этом случае 
.
Таким образом:
Если 
,
то
здесь 
означает знак
числа.
Таким образом:
