численные методы / метод ньютона

Метод Ньютона

Материал из Википедии — свободной энциклопедии

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный методнахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономомИсааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.

Описание метода

Обоснование

Чтобы численно решить уравнение  методом простой итерации, его необходимо привести к следующей форме: , где  — сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения  должно выполняться условие . Решение данного уравнения ищут в виде , тогда:

В предположении, что точка приближения «достаточно близка» к корню , и что заданная функция непрерывна , окончательная формула для такова:

С учётом этого функция  определяется выражением:

Эта функция в окрестности корня осуществляет сжимающее отображение^[1], и алгоритм нахождения численного решения уравнения  сводится к итерационной процедуре вычисления:

По теореме Банаха последовательность приближений стремится к корню уравнения .

Иллюстрация метода Ньютона (синим изображена функция , нуль которой необходимо найти, красным — касательная в точке очередного приближения ). Здесь мы можем увидеть, что последующее приближение  лучше предыдущего .

Геометрическая интерпретация

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть  — определённая на отрезке идифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:

где  — угол наклона касательной в точке .

Следовательно искомое выражение для  имеет вид:

Итерационный процесс начинается с некоего начального приближения  (чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).

Алгоритм

1. Задается начальное приближение .

2. Пока не выполнено условие остановки, в качестве которого можно взять  или  (то есть погрешность в нужных пределах), вычисляют новое приближение: .

Пример

Иллюстрация применения метода Ньютона к функции  с начальным приближением в точке .
График последовательных приближений.	График сходимости.
Согласно способу практического определения скорость сходимости может быть оценена как тангенс угла наклона графика сходимости, то есть в данном случае равна двум.

Рассмотрим задачу о нахождении положительных , для которых . Эта задача может быть представлена как задача нахождения нуля функции . Имеем выражение для производной . Так как  для всех  и  для , очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение , тогда:

Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.

[править]Условия применения

Иллюстрация расхождения метода Ньютона, применённого к функции  с начальным приближением в точке .

Рассмотрим ряд примеров, указывающих на недостатки метода.

Контрпримеры

• Если начальное приближение недостаточно близко к решению, то метод может не сойтись.

Пусть

Тогда

Возьмём нуль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст нуль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.

График производной функции  при приближении  к нулю справа.

• Если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня.

Рассмотрим функцию:

Тогда  и  всюду, кроме 0.

В окрестности корня производная меняет знак при приближении к нулю справа или слева. В то время, как  для .

Таким образом  не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне,  бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.

• Если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена.

Рассмотрим пример:

Тогда  и  за исключением , где она не определена.

На очередном шаге имеем :

Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и  бесконечно дифференцируема везде, кроме как в корне.

• Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.

Пусть

Тогда  и следовательно . Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.

Ограничения

Пусть задано уравнение , где  и надо найти его решение.

Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).

Теорема Канторовича.

Если существуют такие константы , что:

1.  на , то есть  существует и не равна нулю;

2.  на , то есть  ограничена;

3.  на , и ;

Причём длина рассматриваемого отрезка . Тогда справедливы следующие утверждения:

1. на 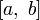 существует корень  уравнения ;

2. если , то итерационная последовательность сходится к этому корню: ;

3. погрешность может быть оценена по формуле .

Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:

Тогда ограничения на исходную функцию  будут выглядеть так:

1. функция должна быть ограничена;

2. функция должна быть гладкой, дважды дифференцируемой;

3. её первая производная  равномерно отделена от нуля;

4. её вторая производная 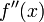 должна быть равномерно ограничена.