численные методы / многочлен чебышева

Многочлены Чебышева

Многочле́ны Чебышева — две последовательности ортогональных многочленов  и , названные в честь Пафнутия Львовича Чебышева. Многочлены Чебышева играют важную роль в теории приближений, поскольку корни многочленов Чебышева первого рода используются в качестве узлов в интерполяции алгебраическими многочленами.

Многочлены Чебышева первого рода

Многочлен Чебышева первого рода  характеризуется как многочлен степени  со старшим коэффициентом , который меньше всего отклоняется от нуля на интервале . Впервые рассмотрены самим Чебышёвым.

Многочлены Чебышева второго рода

Многочлен Чебышева второго рода  характеризуется как многочлен степени  со старшим коэффициентом , интеграл отабсолютной величины которого по интервалу  принимает наименьшее возможное значение. Впервые рассмотрены в совместной работе двух учеников Чебышева — Коркина и Золотарёва.

Рекурсивное определение

Многочлены Чебышева первого рода  могут быть определены с помощью рекуррентного соотношения:

Многочлены Чебышева второго рода  могут быть определены с помощью рекуррентного соотношения:

Явные формулы

Многочлены Чебышева являются решениями уравнения Пелля:

в кольце многочленов с вещественными коэффициентами и удовлетворяют тождеству:

Из последнего тождества также следуют явные формулы:

Тригонометрическое определение

Многочлены Чебышева первого рода  могут быть также определены с помощью равенства:

или, что почти эквивалентно,

Многочлены Чебышева второго рода  могут быть также определены с помощью равенства:

Несколько первых многочленов Чебышева первого рода

Несколько первых многочленов Чебышева второго рода

Свойства

Многочлены Чебышева обладают следующими свойствами:

• Многочлены чётных степеней являются чётными функциями, нечётных — нечётными функциями.

• Сумма коэффициентов многочленов Чебышева первого рода  равняется 1, а коэффициентов многочленов второго рода  равняется .

• Ортогональность по отношению к соответствующим скалярному произведению (с весом  для многочленов первого рода и  для многочленов второго рода).

• Среди всех многочленов, значения которых на отрезке  не превосходят по модулю 1, многочлен Чебышева имеет:

  • наибольший старший коэффициент

  • наибольшее значение в любой точке за пределами 

  • если 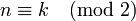, то , где  — коэффициент многочлена Чебышева первого рода,  — коэффициент любого из рассматриваемых полиномов.

• Нули полиномов Чебышева являются оптимальными узлами в различных интерполяционных схемах. Например, в методе дискретных особенностей, который часто используется при исследовании интегральных уравнений в электродинамике и аэродинамике.

• На концах и середине отрезка выполняются следующие соотношения:

• Многочлен Чебышева первого рода порядка N является частным случаем фигур Лиссажу при соотношении частот, равном N и амплитуде обоих сигналов, равной 1.

[править]Свойства

Многочлены Чебышева обладают следующими свойствами:

• Многочлены чётных степеней являются чётными функциями, нечётных — нечётными функциями.

• Сумма коэффициентов многочленов Чебышева первого рода  равняется 1, а коэффициентов многочленов второго рода  равняется .

• Ортогональность по отношению к соответствующим скалярному произведению (с весом  для многочленов первого рода и  для многочленов второго рода).

• Среди всех многочленов, значения которых на отрезке  не превосходят по модулю 1, многочлен Чебышева имеет:

  • наибольший старший коэффициент

  • наибольшее значение в любой точке за пределами 

  • если , то , где  — коэффициент многочлена Чебышева первого рода,  — коэффициент любого из рассматриваемых полиномов.

• Нули полиномов Чебышева являются оптимальными узлами в различных интерполяционных схемах. Например, в методе дискретных особенностей, который часто используется при исследовании интегральных уравнений в электродинамике и аэродинамике.

• На концах и середине отрезка выполняются следующие соотношения:

• Многочлен Чебышева первого рода порядка N является частным случаем фигур Лиссажу при соотношении частот, равном N и амплитуде обоих сигналов, равной 1.

[править]Применения

Многочлены Чебышева применяются для расчета антенной решётки. Мощность излучения каждой антенны рассчитывается при помощи многочленов Чебышева. Это позволяет управлять формой диаграммы направленности, а точнее соотношением амплитуды основного и боковых лепестков.