14. Многоскоростные системы. Система однократной интерполяции.

Про многоскоростные системы написано в вопросе 13. Здесь будет только система однократной интерполяции.

Система однократной интерполяции включает в себя два блока (рис. 19.1):

экспандер;

цифровой ФНЧ.

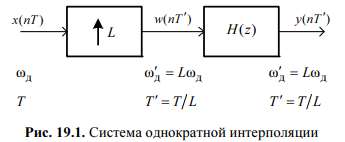
Экспандер (блок со стрелкой вверх) формирует промежуточный сигнал w(nT′) с периодом дискретизации T′=T/L (частотой дискретизации ) путем добавления (L-1) равноотстоящих нулей на каждом периоде дискретизации T входного сигнала x(nT):

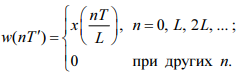
Соотношение между периодами дискретизации входного x(nT) и промежуточного w(nT′) сигналов позволяет интерпретировать "новую" шкалу nT′ как растяжение "старой" шкалы nT в L раз (рис. 19.2, а, б).

Соотношение между частотами дискретизации спектральных плотностей данных сигналов позволяет интерпретировать "новую" шкалу ω′ , напротив, как сжатие "старой" шкалы ω в L раз (рис. 19.3, а, б).

Цифровой ФНЧ предназначен для подавления (L-1) "лишних" составляющих спектральной плотности промежуточного сигнала на периоде , следовательно, его идеальная АЧХ в основной полосе частот шкалы ω′ должна удовлетворять требованиям (рис. 19.3, в):

или в шкале частот ω :

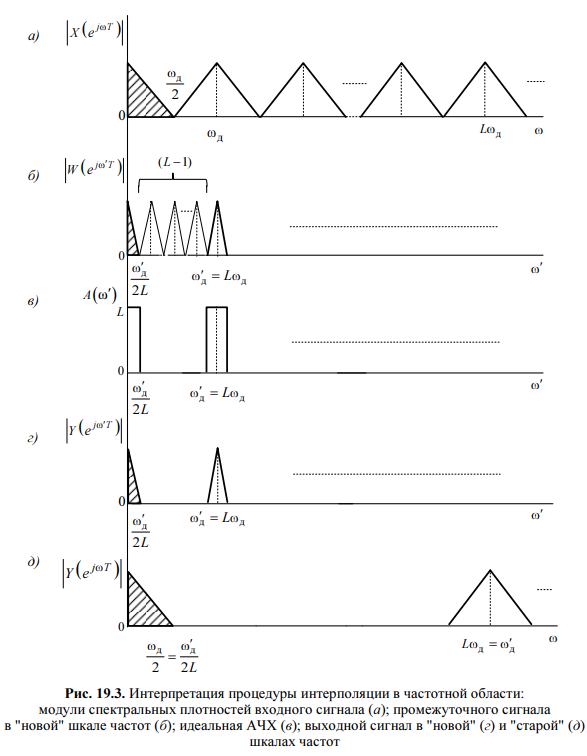
На рис. 19.2, в и рис. 19.3, г изображены выходной сигнал y(nT′) и модуль его спектральной плотности , а на рис. 19.2, г и рис. 19.3, д — они же в "старых" шкалах времени nT и частот ω . Период дискретизации выходного сигнала уменьшился, а частота дискретизации увеличилась в L раз.

Модули спектральной плотности дискретного сигнала на выходе ФНЧ (см. рис. 19.3, г) и спектральной плотности дискретного сигнала, которая была бы получена путем непосредственной дискретизации исходного аналогового сигнала с частотой , совпадают с точностью до множителя L , а аргументы различаются .

В действительности АЧХ не идеальна, поэтому аргументы и модули спектральных плотностей могут отличаться. Для сохранения формы исходного сигнала (исключения влияния фазовых искажений) в качестве ФНЧ выбирают КИХ-фильтр с линейной ФЧХ. С учетом (19.3), соотношение вход/выход системы интерполяции в z-области имеет вид:

, где:

при подстановке n=Lm

15. Многоскоростные системы. Система однократной передискретизации.

Про многоскоростные системы написано в вопросе 13. Здесь будет только система однократной передискретизации.

Система однократной передискретизации представлена на рис. 19.7. Повышение или понижение частоты дискретизации на коэффициент передискретизации в виде рациональной дроби L/M реализуется каскадным соединением систем интерполяции с коэффициентом L и децимации с коэффициентом M (рис. 19.7, а). В результате объединения двух каскадно включенных ФНЧ — блоков — работающих на одинаковой частоте дискретизации Lωд, переходят к системе однократной передискретизации с единственным ФНЧ (рис. 19.7, б). Его идеальная АЧХ, должна удовлетворять требованиям:

16. Полифазная структура системы однократной интерполяции.

Полифазные структуры систем однократной интерполяции и децимации предназначены для повышения быстродействия многоскоростных систем и основаны на замещении одного сложного КИХ-фильтра ФНЧ, работающего на "высокой" частоте дискретизации, эквивалентной системой более простых КИХ-фильтров ФНЧ, работающих на "низкой" частоте.

Идея построения полифазных структур основана на использовании двух замечательных тождеств

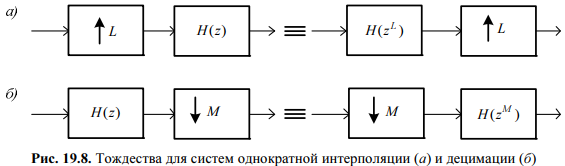
Замечательному тождеству на рис. 19.8, а соответствует тождество для соотношения вход/выход

Оно означает, что сначала можно выполнить фильтрацию входного сигнала с "низкой" частотой дискретизации КИХ-фильтром с передаточной функцией с "низкой" частотой дискретизации, в L раз меньшей, чем у КИХ-фильтра с передаточной функцией H(z) . Тем самым исключается обработка (L-1) промежуточных нулей, которые затем, при переходе к "высокой" частоте дискретизации, добавляются с помощью экспандера.

Эта идея реализована в полифазной структуре однократной системы интерполяции.

Для ее формирования запишем передаточную функцию КИХ-фильтра длины N :

разобьем сумму из N слагаемых на G=N/L (целое число) сумм из L слагаемых и используем матричное представление передаточной функции H(z) в виде произведения матрицы A размером G×L на вектор-столбец B′ длины L :

Здесь

Представим произведение AB′ — вектор-столбец — в виде вектора-строки BA′ с теми же элементами (см. разд. 2.1.4.1)

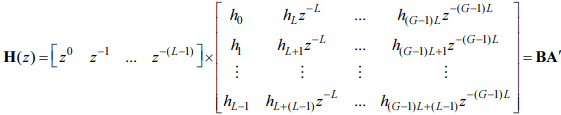
Здесь строки матрицы длины G соответствуют передаточным функциям , ,КИХ-фильтров длины G , что позволяет перейти к записи H(z) в виде произведения векторов:

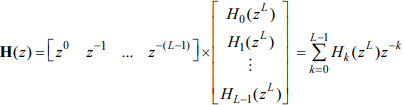
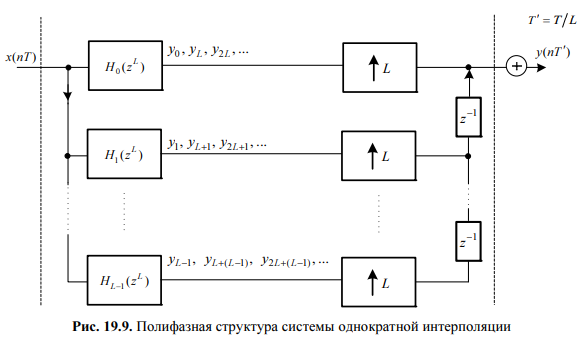
Представление передаточной функции H(z) в виде суммы соответствует параллельной структуре КИХ-фильтров длины G с передаточными функциями , и базовым элементом задержки между ними (рис. 16.9). Такое представление H(z) называют полифазным, соответствующую структуру — полифазной, ее ветви — фазами, а КИХ-фильтры с передаточными функциями ,— полифазными фильтрами.

Переход к "высокой" частоте дискретизации реализуется добавлением экспандеров после фильтрации (см. рис. 19.9).

Z-изображение реакции равно и имеет полифазное представление:

ВАРИАНТ БОЙЧИКА