4. Теорема Котельникова в частотной области. Восстановление аналогового сигнала по отсчётам дпф. Усечённый ряд Котельникова.
Теорема
Котельникова в частотной
области:
непрерывная спектральная плотность
финитного сигнала длительности
может
быть точно восстановлена по своим
отсчетам с периодом дискретизации по
частоте
(или
)
%%%
СПРАВКА:
Есть
иная трактовка т.Котельникова в частотной
области https://circuits-signals.narod.ru/part25.pdf
///
Теорема
Котельникова во временной
области:
непрерывный сигнал с финитной спектральной
плотностью «длительности»
может быть точно восстановлен по своим
отсчетам с периодом дискретизации по
времени
.
///
Вопрос о достаточности точек N дает теорема Котельникова в частотной области, симметричная теореме Котельникова во временной области.
%%%
Восстановление аналогового сигнала
Дискретное
преобразование Фурье X(k) может
использоваться для восстановления
аналогового периодического сигнала с
финитным спектром, расположенным в
области
при N — четном и в области
—
при N нечетном, по формуле (усеченный
ряд Фурье)
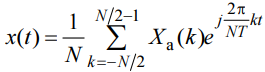
где
отсчеты Xa(k)
связаны с отсчетами ДПФ X(k) соотношением:
Тот же результат будет получен при восстановлении аналогового сигнала непосредственно с помощью усеченного ряда Котельникова:
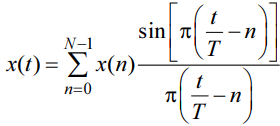
5. Разрешение по частоте. Восстановление спектральной плотности конечной последовательности.
Разрешение
по частоте,
под которым понимают минимальное
расстояние между дискретными гармониками
в ДПФ, определяется исключительно
периодом дискретизации по частоте
и при фиксированной частоте fд
зависит только от длины (периода)
последовательности, поскольку именно
она и только она определяет спектральный
состав (дискретные гармоники)
последовательности.
Восстановление спектральной плотности:
(можно
добавить):
Под восстановлением спектральной
плотности
понимают вычисление ее отсчетов в
промежутке между отсчетами ДПФ, т. е. в
L > N равноотстоящих точках на периоде
ωд:
(формула
(0))
Спектральная плотность конечной последовательности x(n) длины N :
на
периоде
связана
с отсчетами ДПФ
соотношением
Значения спектральной плотности в L равноотстоящих точках на периоде ωд при L>N определяются по формуле:
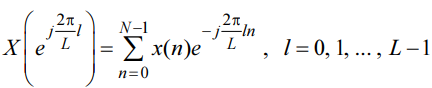(0)
где
l — дискретная нормированная частота,
а Δω — период дискретизации по частоте:
Тот же результат будет получен, если конечную последовательность x(n) длины N дополнить нулями до длины L :
(1)
и
найти ее ДПФ, заменяя N на L :
(2)
С учетом (1) формула (2) принимает вид (солонина предлагает сравнить с формулой (0)):
Увеличение
длины конечной последовательности за
счет добавления (L − N) нулей и,
соответственно, уменьшение периода
дискретизации по частоте до
,
не меняет разрешения по частоте, а лишь
улучшает условия различения близко
расположенных частот дискретных
гармоник.
6. Выделение гармоник полезного сигнала по отсчётам дпф. Первый и второй критерии. Выбор значений порогов по первому и второму критериям.
При вычислении ДПФ часто ставится задача автоматического определения значений модуля ДПФ |X(k)| , превосходящих некоторый заданный порог ε , и соответствующих дискретных нормированных частот k . Фактически, эта задача сводится к выделению полезного сигнала в его аддитивной смеси с шумом. В учебных целях мы ограничимся рассмотрением двух наиболее простых критериев, согласно которым значение модуля ДПФ X(k) аддитивной смеси сигнала с шумом относят к полезному сигналу:
первый критерий — при заданном пороге ε1 значение модуля ДПФ X(k) относят к полезному сигналу, если выполняется условие:
второй критерий — при заданном пороге ε2 значение модуля ДПФ |X(k)| относят к полезному сигналу, если выполняется условие:
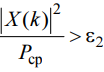
где Pср — средняя мощность аддитивной смеси сигнала с шумом:
Значение порога ε1 в первом критерии задается в пределах:
(1)
а порога ε2 во втором критерии — в пределах:
(2)
при
условии, что
Граничные значения порогов в (1) и (2) можно определить только при априорно известных сигнале и шуме либо их моделях.
При обработке реальных сигналов значение порога ε1 или ε2 задается исходя из требований конкретной задачи.