39. Алгоритм lms. Достоинства и недостатки.
В алгоритме LMS в качестве критерия наилучшего приближения выходного сигнала к образцовому сигналу выбирается минимум квадрата сигнала ошибки (17.2) —(17.3):
.
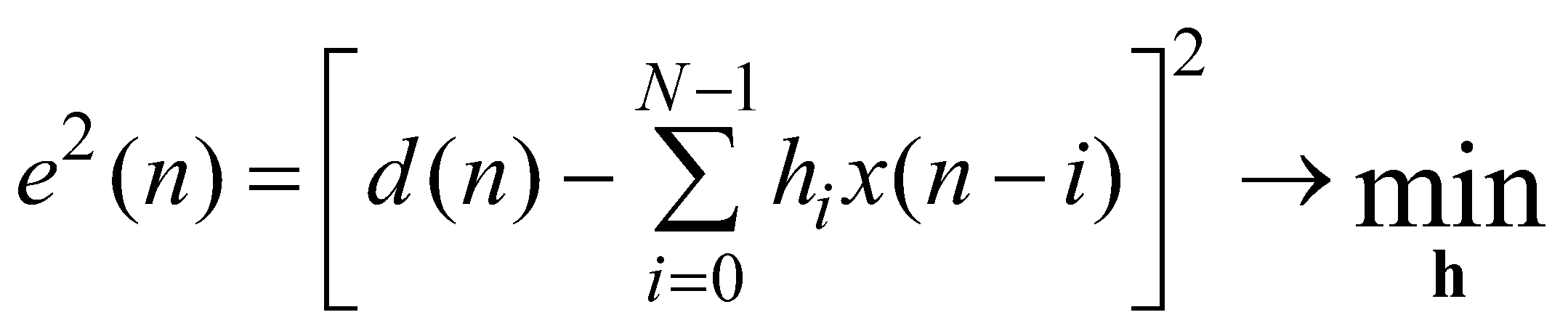Вектор
находится в результате решения
оптимизационной задачи — поиска
минимума функции
,
которая зависит от
времени:
.
Для поиска минимума используют итерационную (пошаговую) процедуру.
На
каждом шаге вычисляется
- вектор
оценок
параметров АФ, смещаемый относительно
вектора
на величину, пропорциональную градиенту
функции
:
,
(17.11)
где
—
шаг
адаптации
(задается пользователем).
Градиентом функции называют ее частные производные по всем :
,
.
В квадратных скобках имеем частные производные данной функции по всем i h в момент времени n:
.
Подставляя в (17.11), получаем рекуррентную формулу:
,
(17.12)
где
—
вектор отсчетов входного сигнала
.
Начальные
значения параметров АФ
по
умолчанию нулевые.
Шаг адаптации выбирается из условия
,
(17.13)
где:
—
среднеквадратичное
значение входного сигнала
длины L;
— длина КИХ-фильтра
Значение шага адаптации выбирают из компромиссных соображений:
скорость сходимости оценки параметров АФ (скорость приближения к оптимальным параметрам
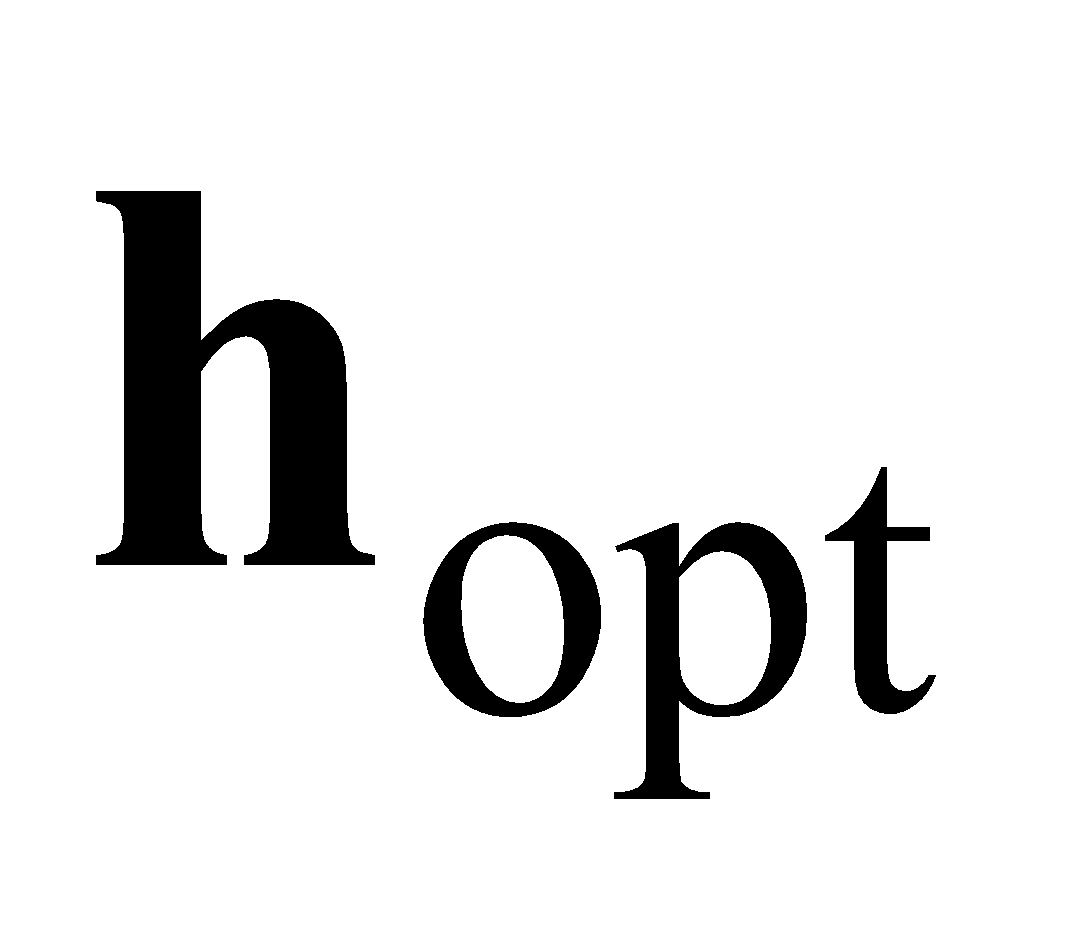в фильтре Винера) с ростом
растет и скорость сходимости;но одновременно с ростом начинает расходиться значение дисперсии сигнала ошибки по сравнению с фильтром Винера, для которого она минимальна.
Обычно значение выбирают равным половине максимального шага в (17.13).
Если значение средней мощности невозможно оценить заранее, используют модификацию алгоритма LMS — нормированный алгоритм NLMS, где шаг адаптации зависит от времени:
.,
Шаг
нормируется к энергии сигнала
на текущем интервале
:
,
где
—
энергия сигнала (произведение строки
на столбец);
—
фиксированное значение шага, влияющее
на сходимость алгоритма адаптации,
обычно
;
—
малая положительная константа,
определяющая максимальное значение
при нулевом сигнале.
В начале процесса адаптации наблюдается переходный процесс, когда дисперсия сигнала ошибки много большей, чем по его окончании — в установившемся режиме.
Достоинство алгоритма LMS — простота: на каждом шаге в (17.12) выполняется N операций умножения-сложения.
Недостаток алгоритма LMS —относительно медленная сходимость к оптимальным параметрам : длина переходного процесса и дисперсия сигнала ошибки, больше, чем в алгоритме RLS.
40. Алгоритм rls. Достоинства и недостатки.
В алгоритме LMS в качестве критерия наилучшего приближения выходного сигнала к образцовому сигналу выбирается минимум суммы квадратов сигнала ошибки (17.2) —(17.3):
.
Вектор
находится в результате решения
оптимизационной задачи — поиска
минимума целевой функции
,
которая не зависит от
времени:
Минимум достигается при равенстве нулю частных производных по всем :
.
Выполним замену в вне квадратных скобок:
.
Перенесем сумму с неизвестными параметрами в левую часть:
.
Получили
соотношение, совпадающее с точностью
до множителя
с соотношением (17.6) для фильтра Винера.
Следовательно, на его основе могут быть
получены параметры АФ
При этом отсутствие множителя (усреднения) означает, что не требуется вычислять АКФ, а можно использовать непосредственно отсчеты сигналов и .
Вывод рекуррентной формулы для вычисления параметров АФ достаточно сложен и приводится в новой книге.
Достоинство алгоритма RLS — оптимальные параметры АФ в установившемся режиме. Длительность переходного процесса, быстрее, чем в LMS, а дисперсия сигнала ошибки установившемся режиме, минимально достижимая.
Недостаток алгоритма RLS — существенно больший объем вычислений, следовательно, большая вычислительная сложность по сравнению с алгоритмом LMS.
