31. Влияние порядка ар-модели на оценку спм. Критерий Байеса.

Порядок АР-модели (M−1)обычно заранее неизвестен, поэтому приходится испытывать его различные значения. Заниженный порядок АР-модели может привести к сглаживанию оценки СПМ (неразличимости малых пиков), а завышенный — к появлению ложных пиков, наряду с возрастанием трудоемкости оценки параметров при большом порядке СЛАУ и риском неустойчивости ее решения при плохо обусловленной матрице коэффициентов.

Поэтому при выборе порядка АР-модели приходится искать компромисс между уменьшением среднего квадрата ошибки линейного предсказания и увеличением порядка модели. Для оптимальной оценки порядка АР-модели анализируемой последовательности можно воспользоваться информационными критериями. Одним из простейших является информационный критерий Байеса (BIC):

где L — длина последовательности; p = (M - 1) — порядок АР-модели; — средний квадрат ошибки линейного предсказания;

Задача определения оптимального порядка popt сводится к поиску порядка , при котором достигается минимум функции:

Минимальный pmin и максимальный pmax порядки обычно выбираются из эмпирических соображений, и для каждого порядка p рассчитывается .

32. Влияние длины последовательности на оценку спм параметрическими методами.

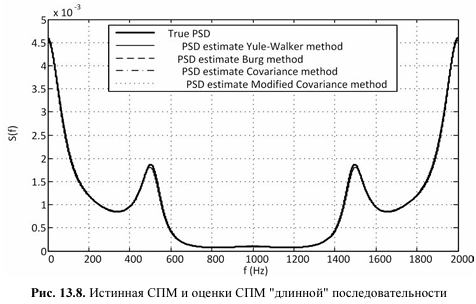
На рис. 13.8 представлены истинная СПМ "длинной" последовательности длины N=10000 и различные оценки СПМ на периоде fд=2000 Гц, которые практически совпали

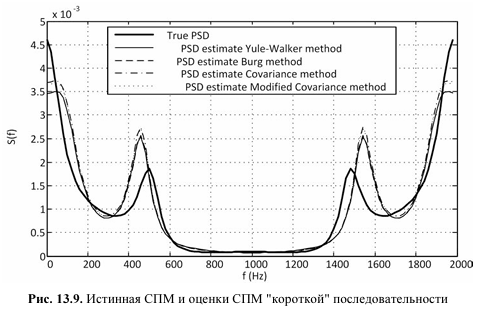
На рис. 13.9 представлены истинная СПМ "короткой" последовательности длины N = 100 и различные оценки СПМ на периоде д 2000 fд = 2000 Гц. В оценках СПМ проявились аномалии: смещение пиков и впадин и искажение их значений.

33. Адаптивный фильтр. Структура аф.

Использование традиционных ЦФ — КИХ- и БИХ-фильтров с постоянными коэффициентами — основано на предположении, что полосы частот полезного сигнала и шума известны и разнесены, поэтому коэффициенты ЦФ могут быть определены до обработки входного сигнала.

Однако во многих случаях входной сигнал не адекватен подобной модели, поэтому коэффициенты ЦФ невозможно определить заранее. В подобных случаях применяют адаптивные фильтры.

Адаптивным фильтром (АФ) называют систему, параметры которой адаптируются (подстраиваются) к сигналу с заранее неопределенной статистической моделью в процессе его обработки.

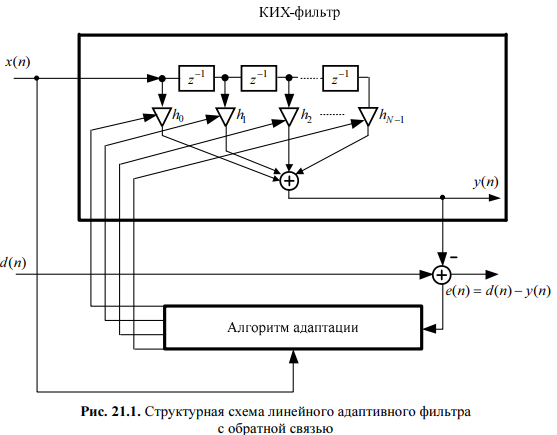
Среди адаптивных фильтров наибольшее распространение получили линейные адаптивные фильтры с обратной связью, реализованные на основе КИХ-фильтров.

Структурная схема (структура) такого АФ представлена на рис. 21.1.

Адаптивный фильтр включает в себя (см. рис. 21.1):

КИХ-фильтр;

алгоритм адаптации.

Параметрами АФ называют коэффициенты КИХ-фильтра, подстраиваемые к входному сигналу.

По определению, параметры АФ изменяются в процессе адаптивной фильтрации.

На вход АФ одновременно поступают два сигнала (см. рис. 21.1):

входной сигнал x(n) — заранее неизвестный;

образцовый сигнал (desired signal) d(n) — заранее известный.

Пока мы не ставим вопрос о получении образцового сигнала, а лишь констатируем его доступность в ряде задач, решаемых средствами адаптивной фильтрации.

Сигнал x(n) подается одновременно на вход КИХ-фильтра и алгоритма адаптации.

На выходе АФ формируются два сигнала:

- выходной сигнал y(n) .

Согласно разностному уравнению (РУ), выходной сигнал КИХ-фильтра равен линейной комбинации отсчетов входного сигнала:

где — коэффициенты КИХ-фильтра.

Напомним, что коэффициенты РУ КИХ-фильтра совпадают с отсчетами его импульсной характеристики (ИХ);

- сигнал ошибки e(n) — разность между образцовым и выходным сигналами

Согласно (21.1), сигнал ошибки равен

Под линейностью АФ понимают линейность входящего в его состав КИХ-фильтра. Для любого фиксированного набора коэффициентов КИХ-фильтр представляет собой линейную дискретную систему (ЛДС), которая удовлетворяет условиям аддитивности и однородности. Соотношение вход/выход ЛДС описывается линейным РУ с постоянными коэффициентами hi .

Однако в процессе адаптивной фильтрации параметры АФ (набор фиксированных коэффициентов КИХ-фильтра) изменяются во времени, подстраиваясь к входному сигналу с помощью алгоритма адаптации. Соотношение вход/выход АФ принимает вид нелинейного РУ с переменными коэффициентами hi(n):

и АФ не удовлетворяет условиям аддитивности и однородности, а следовательно, представляет собой нелинейную систему обработки сигналов.

Таким образом, в каждый момент времени n КИХ-фильтр в составе АФ имеет фиксированные коэффициенты и представляет собой линейную систему, однако в целом в процессе адаптации АФ функционирует как нелинейная система.

Обратная связь в традиционном ЦФ - связь текущего значения выходного сигнала с его предшествующими значениями, что имеет место только в БИХ-фильтрах. В АФ обратная связь - связь алгоритма адаптации с сигналом ошибки e(n) , на основе которой подстраиваются коэффициенты КИХ-фильтра (изменяются параметры АФ).

Устойчивость алгоритма адаптации - сходимость вычисляемых параметров АФ к оптимальным (по заданному критерию) параметрам. При этом для входящего в состав АФ КИХ-фильтра устойчивость гарантируется для любого набора фиксированных коэффициентов.

Целью адаптивной обработки - обеспечение наилучшего приближения выходного сигнала y(n) к образцовому сигналу d(n) по заданному критерию.

Основная сложность в проектировании АФ связана с разработкой алгоритмов адаптации.

34. Задача идентификации неизвестной системы + структурная схема.

Решение многих задач с применением АФ (рис. 17.1) основано на идентификации неизвестной системы.

Под идентификацией неизвестного объекта понимают его совпадение или сходство (по заданному критерию) с известным объектом.

Под идентификацией неизвестной системы понимают понимают совпадение или сходство (по заданному критерию) ее входного и выходного сигналов с входным и выходным сигналами известной системы.

В качестве известной системы используется АФ.

Различают две разновидности идентификации систем: прямая и обратная.

При прямой идентификации (рис. 17.3) входные сигналы неизвестной системы и АФ совпадают. В качестве образцового сигнала для АФ используется выходной сигнал

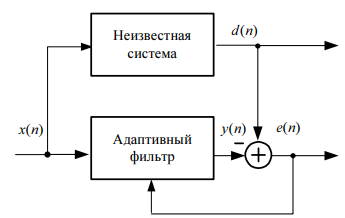
Рис. 17.3. Структурная схема системы прямой идентификации

В процессе адаптации АФ стремится преобразовать входной сигнал так, чтобы обеспечить наилучшее приближение выходного сигнала АФ к выходному сигналу неизвестной системы d(n) по заданному критерию и решение задачи прямой идентификации сводится к определению параметров АФ, при которых это обеспечивается.

При обратной идентификации (рис. 17.4) выходной сигнал неизвестной системы совпадает с входным сигналом АФ. В качестве образцового сигнала для АФ используется входной сигнал неизвестной системы d(n).

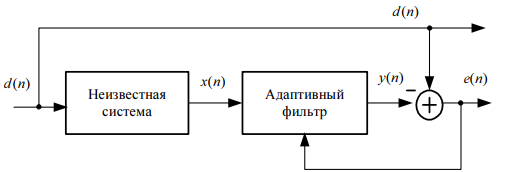
Рис. 17.4. Структурная схема системы обратной идентификации

В процессе адаптации АФ стремится преобразовать входной сигнал так, чтобы обеспечить наилучшее приближение выходного сигнала АФ к входному сигналу неизвестной системы по заданному критерию.

35. Задача оценки сигнала от шума + структурная схема.

Выделение полезного сигнала в его аддитивной смеси с шумом — очистка сигнала от шума — сводится к решению задачи прямой идентификации (рис. 17.5).

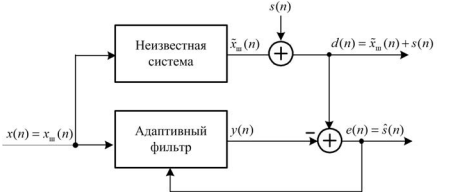
Рис. 17.5. Структурная схема системы прямой идентификации при очистке сигнала от шума

Входные сигналы неизвестной системы и АФ совпадают и представляют собой шум , доступный для наблюдения.

Выходной сигнал неизвестной системы представляет собой искаженный шум . Это шум , измененный под влиянием каких-либо факторов, например, внешней среды. При моделирование его получают, пропуская шум через КИХ- или БИХ фильтр.

Образцовый сигнал представляет собой аддитивную смесь полезного сигнала с искаженным шумом :

.

Шум коррелированный с шумом , но не коррелирован с сигналом .

Сигнал ошибки равен

.

В процессе адаптации АФ стремится преобразовать входной сигнал так, чтобы обеспечить наилучшее приближение выходного сигнала АФ к искаженному шуму (поскольку полезный сигнал не коррелирован с входным шумом ), и по завершении процесса адаптации будет получена его оценка:

,

а сигнал ошибки будет представлять собой оценку полезного сигнала:

.

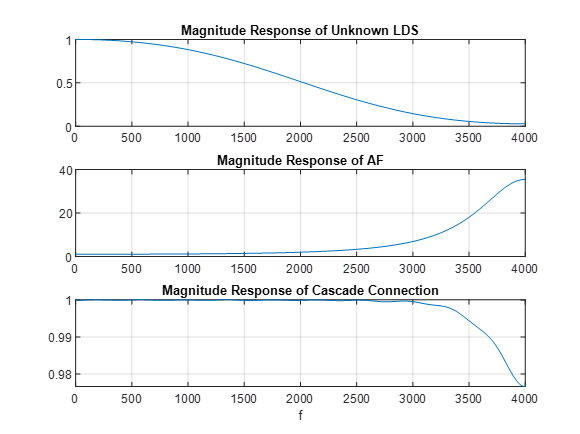
36. Задача выравнивания ЧХ + структурная схема.

Постановка задачи: имеется случайный сигнал с широкой полосой пропускания. При прохождении по каналу связи (неизвестной системе) полоса пропускания ограничивается. Требуется ее расширить на приемной стороне .

Эта задача решается путем выравнивания частотной характеристики неизвестной системы на основе ее обратной идентификации (рис. 17.6).

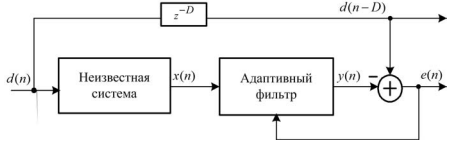
Рис. 17.6. Структурная схема системы обратной идентификации для выравнивания ЧХ неизвестной системы

Выходной сигнал неизвестной системы совпадает с входным сигналом АФ.

В качестве образцового сигнала АФ используется входной сигнал неизвестной системы d(n), задержанный на D отсчетов — d(n-D).

Неизвестная система (канал связи, ограничивающий полосу) моделируется с помощью КИХ-фильтра ФНЧ (или ПФ). Длина данного КИХ-фильтра существенно меньше длины КИХ-фильтра в составе АФ.

Задержка используется для согласования времени прохождения сигналов

Значение задержки обычно выбирают равной или больше половины длины КИХ-фильтра — .

В процессе адаптации АФ стремится преобразовать входной сигнал так, чтобы обеспечить наилучшее приближение выходного сигнала АФ к входному сигналу неизвестной системы , и по завершении процесса адаптации будет получена его оценка:

. (17.14)

По определению передаточные функции неизвестной системы и АФ равны:

; ,

а передаточная функция их каскадного соединения равна произведению передаточных функций неизвестной системы G(z) и АФ H(z) :

.

Согласно , z-изображение выходного сигнала АФ (17.14) равно

,

следовательно, передаточная функция АФ равна

,

а передаточная функция каскадного соединения равна

, (17.15)где  — оценка z-изображения цифрового единичного импульса .

Подставляя , получим частотную характеристику каскадного соединения:

,

с выровненной АЧХ и лнейной ФЧХ, где .

На основании (17.15) выходной сигнал каскадного соединения будет равен оценке задержанного цифрового единичного импульса

.

37. Задача оценки параметров линейного предсказания + структурная схема.

Линейным предсказанием сигнала называют оценку его текущего отсчета на основе линейной комбинации предшествующих отсчетов.

Задача линейного предсказания заключается в определении параметров линейного предсказания ,обеспечивающих наилучшее приближение оценки текущего отсчета к его истинному значению x(n) по заданному критерию, в качестве которого выбирается минимум среднего квадрата ошибки линейного предсказания ε(n)

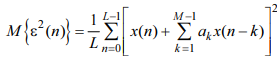
Параметры линейного предсказания ak определяются в результате решения СЛАУ

(1)

и представляют собой оценки параметров АР-модели

Сравним СЛАУ со СЛАУ в фильтре Винера:

Выберем в качестве образцового сигнала АФ d(n) сигнал x(n) , для которого требуется определить параметры линейного предсказания:

а в качестве входного сигнала АФ — задержанный сигнал x(n-1) , и с учетом этого запишем СЛАУ в фильтре Винера

Выполнив замену переменных k=(i+1) , получим: (2)

где выражение в квадратных скобках, соответствует выходному сигналу АФ y(n-1)

Сравним СЛАУ (2) с (1). При совпадении (с точностью до знака) правых частей имеем совпадение левых частей, следовательно, для параметров АФ hi и параметров линейного предсказания справедливо соотношение:

Для случайного сигнала x(n) , статистическая модель которого заранее неизвестна, используют один из алгоритмов рекуррентного вычисления оценок параметров АФ — оценок параметров линейного предсказания.