27. Параметрические методы. Достоинства методов. Этапы расчёта оценки спм.
Параметрические методы оценки СПМ основаны на построении математической модели анализируемой последовательности (эргодического случайного процесса) и оценке параметров модели при которых обеспечивается наилучшее приближение моделируемой последовательности к анализируемой по заданному критерию.
Параметрические методы обеспечивают возможность получения более достоверных оценок СПМ в отсутствие осцилляций (изрезанности) и искажений, связанных с применением окон, характерных для непараметрических методов.
Основная сложность параметрических методов заключается в выборе математической модели, адекватной анализируемой последовательности, и оценке ее параметров.
В зависимости от вида математической модели различают следующие группы параметрических оценивания СПМ:
Авторегрессии скользящего среднего (АРСС) - на основе АРСС-модели
Скользящего среднего (СС)) - на основе СС-модели
Авторегрессионные (АР) - на основе АР-модели
Основная идея параметрических методов заключается в вычислении оценок параметров модели и оценки дисперсии на основе анализируемой последовательности x(n) и использовании формулы
Для расчета ее оценки СПМ
Этапы расчета оценки СПМ:
Выбор мат.модели(АР,СС, АРСС)
Оценка порядка модели
Оценка параметров модели
Расчет оценки дисперсии нормального белого шума
Расчет оценки СПМ
28. Модели параметрических методов и их назначение. Структурная схема и ру этих моделей.
АРСС модель
АРСС-модель описывается разностным уравнением БИХ-фильтра, представленным в виде:
Где :
e(n) - входной сигнал (воздействие), в качестве которого используется белый шум, обычно нормальный с нулевым средним и дисперсией
;y(n) - входной сигнал (реакция) (наверное выходной, хз в книге входной написано) - модель анализируемой последовательности, которую во избежании путаницы, будем называть моделирующей последовательностью;
и
- параметры АРСС-модели, где
(M-1) - порядок АРСС-модели при
по умолчанию
АРСС-модели соответствует БИХ-фильтр с дробно-рациональной передаточной функцией :
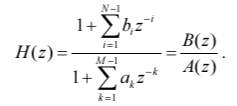
Структураня схема АРСС-модели:
АР-модель
АР-модели соответствует БИХ-фильтр полюсного вида (чисто рекурсивный) с передаточной функцией при b0=1:
Структурная схема АР-модели:
РУ АР-модели:
СС-модель
СС-модели соответствует КИХ-фильтр с передаточной функцией:
РУ СС-модели:
Структурная схема СС-модели:
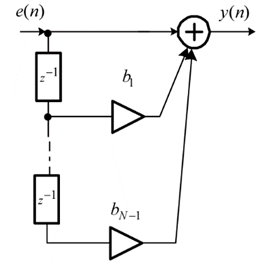
Выбор модели определяется требованиями конкретной задачи и обычно предполагает сведения о возможном характере СПМ.
АР-модель считается наиболее подходящей для оценки СПМ с острыми пиками, но без глубоких впадин, а СС-модель, наоборот - с глубокими впадинами, но без острых пиков точеных и хуёв дроченных
АРСС-модель как наиболее общая, может использоваться для оценки СПМ с пиками и впадинами, однако при наличии острых пиков точенных или хуёв дроченных она обеспечивает меньшую точность чем АР-модель, а при наличии глубоких впадин - меньшую точность чем СС-модель.
По вычислительным затратам наиболее простой будет АР-модель, т.к. Расчет оценок ее параметров сводится к решению системы линейных уравнений , в то время как для СС- АРСС-моделей - к решению нелинейных уравнений.
В общем случае выбору модели должна предшествовать ее проверка на адекватность (как и нас всех) анализируемому сигналу.
На практике наибольшее распространение получила АР-модель, которая далее будет рассматриваться по умолчанию. Это обусловлено ее адекватностью широкому классу реальных сигналов, наименьшими вычислительными затратами и наличием стандартных средств в МАТЛАБЕ БЛЯТЬ для расчетов оценок СПМ