ВОПРОСЫ ПО КУРСУ ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ СЕМЕСТР 2/2 (ОСЕНЬ 2024)
%%%
ЛЕГЕНДА:
заебись,
четко
пиздеж\необходимы
правки (желтые
формулы не считаются!!)
коментарии
%%%
%%%
1. Спектральная плотность конечной последовательности. Ряд Фурье.
Можно и лучше, но думаю норм, там переход на ряд фурье идет
2. Формулы ДПФ и ОДПФ. Свойства ДПФ.
3. ДПФ конечной последовательности. ДПФ периодической последовательности.
4. Теорема Котельникова в частотной области. Восстановление аналогового сигнала по отсчётам ДПФ. Усечённый ряд Котельникова.
(к сожалению я не смог найти про усеченный ряд котельникова инфу, однако некоторое упоминание про это я внес)
5. Разрешение по частоте. Восстановление спектральной плотности конечной последовательности.
6. Выделение гармоник полезного сигнала по отсчётам ДПФ. Первый и второй критерии. Выбор значений порогов по первому и второму критериям.
7. Растекание спектра. Методы борьбы с растеканием спектра.
8. Улучшение различения дискретных гармоник с близко расположенными частотами. Условия для различения дискретных гармоник с близко расположенными частотами.
9. Вычисление круговой и линейной свёртки с помощью ДПФ.
10. Секционированные свёртки. Методы их вычисления.
11. БПФ и ОБПФ. Алгоритм вычисления с прореживанием по времени.
12. БПФ и ОБПФ. Алгоритм вычисления с прореживанием по частоте.
13. Многоскоростные системы. Система однократной децимации.
14. Многоскоростные системы. Система однократной интерполяции.
15. Многоскоростные системы. Система однократной передискретизации.
16. Полифазная структура системы однократной интерполяции.
17. Полифазная структура системы однократной децимации.
18. Банки фильтров. Полифазная структура банка фильтров анализа.
19. Банки фильтров. Полифазная структура банка фильтров синтеза.
20. СПМ. Определение и свойства. Теорема Винера-Хинчина.
21. Обработка случайного процесса ЛДС. Соотношение вход/выход для АКФ и СПМ.
22. Алгоритм моделирования случайного процесса с требуемой АКФ.
23. Основные методы спектрального анализа. Основные показатели качества оценок СПМ.
24. Метод периодограмм. Метод периодограмм Даньелла
25. Метод периодограмм Бартлетта. Метод периодограмм Уэлча.
26. Метод Блэкмана-Тьюки. Спектрограмма.
27. Параметрические методы. Достоинства методов. Этапы расчёта оценки СПМ
28. Модели параметрических методов и их назначение. Структурная схема и РУ этих моделей.
29. Метод Юла-Уолкера. Метод Бёрга. Достоинства и недостатки.
30. Ковариационный метод и модифицированный ковариационный метод. Достоинства и недостатки.
31. Влияние порядка АР-модели на оценку СПМ. Критерий Байеса.
32. Влияние длины последовательности на оценку СПМ параметрическими методами.
33. Адаптивный фильтр. Структура АФ.
34. Задача идентификации неизвестной системы + структурная схема.
35. Задача оценки сигнала от шума + структурная схема.
36. Задача выравнивания ЧХ + структурная схема.
37. Задача оценки параметров линейного предсказания + структурная схема.
38. Фильтр Винера. Достоинства и недостатки.
39. Алгоритм LMS. Достоинства и недостатки.
40. Алгоритм RLS. Достоинства и недостатки.
1. Спектральная плотность конечной последовательности. Ряд Фурье.
Спектральная плотность конечной последовательности
(это из урезанной лекции кока)
Задача:
вычислить СП конечной последовательности
длины N на периоде
Для вычисления по этой формуле необходимо заранее знать количество точек на периоде, однако оно неизвестно т. е. вычисление невозможно выполнить методом прямой подстановки, а значит формула не описывает алгоритм вычисления СП.
Ответ на этот вопрос дает дискретное преобразование Фурье (ДПФ)
Вывод формул ДПФ основан на анализе возможности разложения в ряд Фурье периодической последовательности.
это из лекции DSP_12.pdf
Спектральная плотность конечной последовательности x(n) длины N :
СП — периодическая функция, поэтому она вычисляется на периоде
При этом необходимое количество точек заранее неизвестно, т. е. вычисление невозможно выполнить методом прямой подстановки, а значит формула не описывает алгоритм вычисления СП.
Ряд Фурье
Ряд Фурье непрерывной периодической функции xp(t) с периодом Ts описывается
Разложение в ряд Фурье справедливо для функции xp(t) удовлетворяющей условиям Дирихле (функция xp(t) имеет ограниченную вариацию: определена, однозначна и имеет конечное число экстремумов и разрывов 1-го и 2-го рода).
Xa(k)— коэффициенты Фурье:
где индекс «а» означает «аналоговый»;
Δω
— период дискретизации по частоте:
k
— дискретная нормированная частота:
подобно
дискретному нормированному
времени
(формально
T=1)
Совокупность
коэффициентов Фурье Xa(k)
,
,
называют спектром периодической функции
xp(t)
.
Спектр аналогового периодического сигнала представляет собой бесконечную последовательность в частотной области.
Ряд
Фурье по определению должен быть
абсолютно сходящимся:
2. Формулы дпф и одпф. Свойства дпф.
Дискретным преобразованием Фурье периодической последовательности xp(n) называют пару формул:
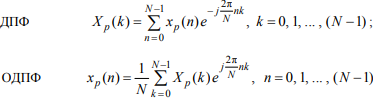
Здесь
вместо
принято
записывать
т. к. где постоянный множитель принято ставить в обратном преобразовании
xp(n)— N-точечная последовательность (один период);
— N-точечное ДПФ (коротко — ДПФ) (один период).
%%%
СПРАВКА:
Совокупность периодических
коэффициентов
называют
спектром периодической последовательности
xp(n)
%%%
Вывод: ДПФ периодической последовательности xp(n) совпадает с ее спектром с точностью до множителя 1/N.
Свойства ДПФ подобны свойствам СП
1. ДПФ — периодическая последовательность с периодом N
2. Линейность.
Если N-точечная последовательность равна линейной комбинации N-точечных последовательностей
,
то ее N-точечное ДПФ равно линейной
комбинации N-точечных ДПФ данных
последовательностей
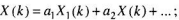
Если в линейной комбинации у последовательностей разные длины
то перед вычислением N-точечного ДПФ
исходные последовательности необходимо
привести к одинаковой длине N дополнив
нулями, где
3.
Сдвиг
(смещение):
,
К
сдвигу приводит умножение N-точечной
последовательности на поворачивающий
множитель
(сдвиг
вправо по оси k на k0
)
или
(сдвиг
влево
)
4. Сдвиг (задержка):
Сдвиг
N-точечной последовательности вправо
на m (m>=0) отсчетов (задержка
последовательности) соответствует
умножению N-точечного ДПФ на поворачивающий
множитель
,
удобно записать так
5.
Равенство
Парсеваля
(для периодических и конченых
последовательностей):
Где
-
энергия сигнала, вычисленная во временной
области
-
та же энергия, вычисленная в частотной
области
6. Свойство симметрии
Если
N-точечная последовательность x(n) -
вещественная, модуль ее N-точечного ДПФ
будет четной функцией переменной k:
А
агрумент - нечетной
Это означает, что для модуля аргумента будут соблюдаться соответственно условия симметрии и антисимметрии
(6-ое свойство взято из курса лекций Солониной 2005г, в книге вроде его нету =\ )
7. Расщепление спектра
8. ДПФ круговой свёртки равняется произведению сворачиваемой последовательности
