1,2 И 3 степени свободы.

Чем сложнее геометрическая фигура, тем большее число степеней свободы у нее.

Базисные функцииsinx/x трудно генерировать, поэтому на практике восстановление непрерывного сообщения по полученным отсчетам выполняется по другим отсчетам, отличным от алгоритма теоремы Котельникова.

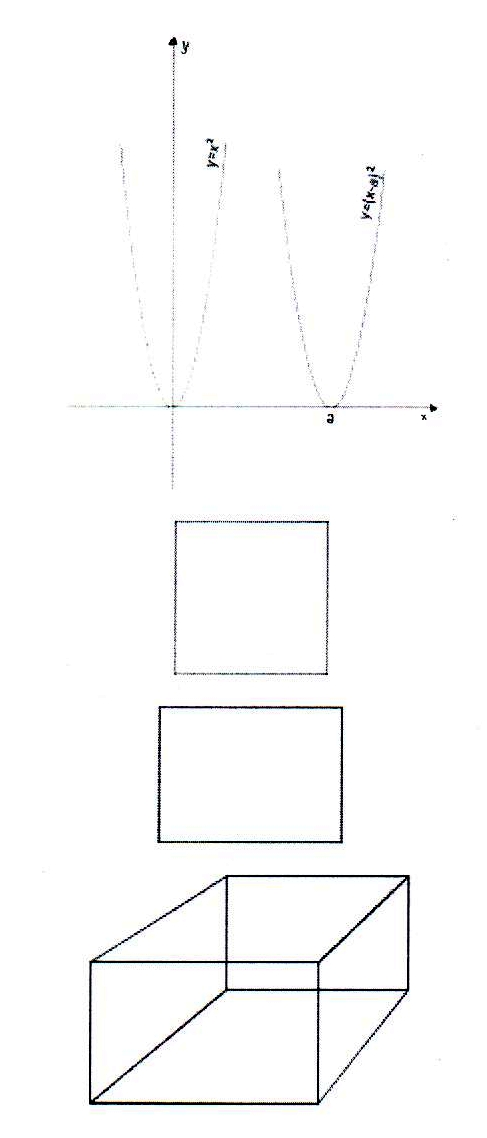
Рисунок.

Чтобы выяснить, какое значение имеет временная функция в момент времени i∆tнужно сложить все составляющие. Из последнего графика видно, что прежде, чем восстанавливать непрерывную функцию λ(t), необходимо получить все ее N отсчетов.

На практике для обеспечения восстановления непрерывной функции но мере получения ее отсчетов используют интервал дискретизации ∆t, на передающей стороне, меньший, чем требуется по теореме Котельникова а на приемной стороне полученные отсчеты подают на низкочастотны фильтр, с выхода которого снимается непрерывное сообщение.

Рисунок.

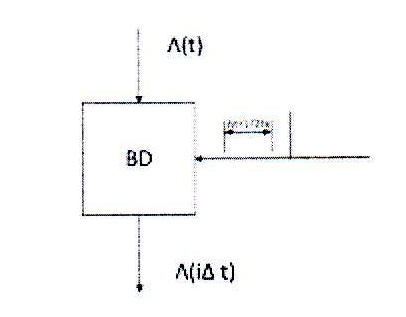
Рисунок.

Полоса пропускания фильтра определяется знамен им частотыf_uв спектре передаваемого сообщения.

Рисунок.

2. Значение теоремы Котельникова

Позволяет осуществить многоканальную передачу сообщений в одном частотном канале связи путем разделения сообщений по времени, то есть между отсчетами одного передаваемого сообщения вставляют отсчеты нескольких других передаваемых сообщений.

10. Общие сведения об РЛС (радиолокационных системах)

1. Сингалы, используемые в радиолокации

1. Видеосигналы

а) Видеоимпульс прямоугольной формы

Рисунок.

Рисунок.

Рисунок.

- форумла, по которой происходит вычисление АКФ.

t_u - длительность импульса.

АКФ показывает степень похожести сигнала S(t) на свою копию, сдвинутую по времени относительно положения сигнала S(t) на интервал времени τ в зависимости от величины этого сдвига τ.

S(t) - сигнал.

S(t-τ) - копия сигнала S(t), сдвинутая на интервал времени τ.

1. τ = -t_u

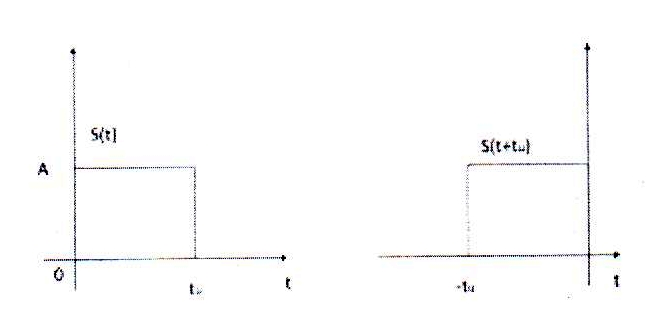
Рисунок.

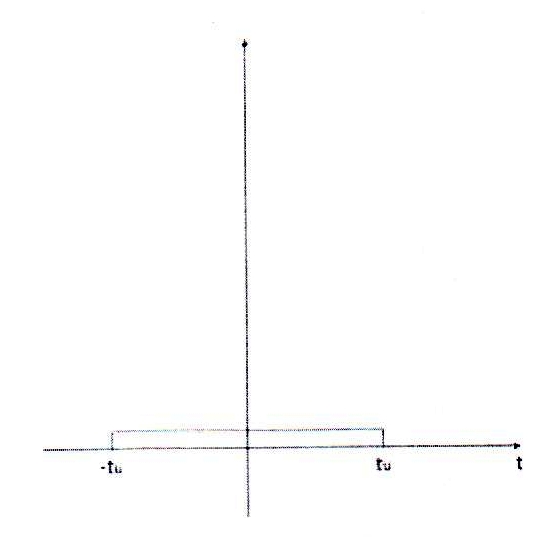
Рисунок.

2. τ = -t_u/2

Рисунок.

Рисунок.

Рисунок.

3. r = 0

Рисунок.

Рисунок.

Рисунок.

4. τ = t_u/2

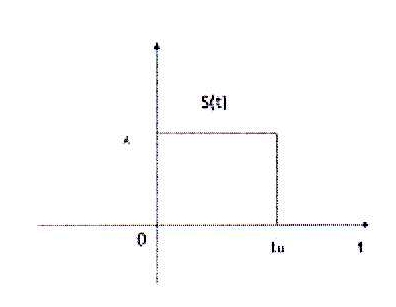
Рисунок.

Рисунок.

Рисунок.

b) Видеоимпульс гауссовой формы

Амплитудно-частотный сиктр(АЧС) a и b – декартовой системе координат.

Рисунок. Рисунок.

(8)

Рисунок.

c) Реальный видеоимпульс прямоугольной формы.

В реальной природе мгновенный рост от 0 до А и мгновенный спад от А до 0 нереальны.

Рисунок

Рисунок Рисунок

d)Последовательность видеоимпульсов прямоугольной формы.

2)Радиоимпульсы.

Рисунок Рисунок

а) Радиоимпульсы с прямоугольной огибающей.

0. <= t<=

A(t) – огибающая прямоугольной формы (только сверху).

A – огибающая сигнала.

ƒ – частота заполнения.

Спектр сплошной и бесконечный.

Чем длиннее сигнал S(5),тем хуже его спектр.

При

Рисунок Рисунок

b) Последовательность радиоимпульсов прямоугольной формы.

Рисунок Рисунок

3) Сложные сигналы

Отличаются от простых наличием внутриимпульсной частотной или фазовой модуляции. В результате чего их база оказывается много больше единицы. База простых сигналов

Сложные сигналы качественно отличаются от простых.

1.ЛЧМ сигнал(сигнал с линейной частотной модуляцией) - девиация частоты.

Автокорреляционная Функция ЛЧМ сигнала.

Рисунок. Рисунок

АКФ ЛЧМ стгнала содержит центральный лепесток и боковые лепестки, которые существенно меньше по амплитуде, чем центральный. Длительность центрального лепестка

Щирина спектра АЧМ сигнала определяется девиацией частоты и не зависит от длительности сигнала.

Рисунок.

Рисунок

2.ФМ сигналы (фазоманипулированные сигналы).

Внутри импульса меняется частота фазы заполнения.

В качестве примера рассмотрен сложный ФМ сигнал с семи элементным кодом Баркера.

Высота всех цоковых треугольников (в 7 раз меньше, чем высота центрального лепестка).

Сложные сигналы позволяют различить два противоречия, которые не могут различить простые сигналы:

1. Они позволяют иметь одновременно хорошую разрешаюшую способность РЛС по длительности и скорости.

2. Позволяют одновременно иметь большую дальность действия РЛС и высокое разрешение по дальности.

Принятые и отраженные от цели сигналы (сложные) усиливаются приемником, которые не изменяют их формы. Затем с выхода приемника сигналы попадают на согласованный фильтр, задача которого максимизировать отношения сигнал-шум на своём выходе в момент окончания приема сигнала. Сигнал на выходе согласованного фильтра является разверткой по времени АКФ принятого сигнала. Максимизация отношения сигнал-шум сигнала нужна для того, чтобы увеличить вероятность правильного обнаружения целей и точность измерения координат.

Рисунок Рисунок

Рисунок