1.3. Основные понятия, используемые для характеристики оценок

Прежде чем переходить к формулировке метода синтеза измерителя "центра пачки", необходимо ознакомиться с основными понятиями, используемыми для характеристики оценок.

Оценка является функцией наблюдаемых выборочных значений , которые используются для определения интересующего нас параметра. Поскольку выборочные значения Y₁ ,Y₂ ,…Y_n являются случайными величинами из-за наличия внутриприёмного шума и флюктуаций отражённого сигнала, то и каждый результат измерения (оценка) является случайной величиной. При измерении азимута, например, искажается огибающая пачки импульсов (рис.7). Центр сглаженной огибающей будет случайной величиной, его положение будет изменяться от пачки к пачке.

В общем случае при оценивании случайная величина оценки меняется от опыта к опыту и не даёт исчерпывающей характеристики алгоритма оценивания.

Качество оценивания полностью определяется лишь распределением оценки . На практике для характеристики оценки часто используются лишь параметры распределения , такие как среднее значение оценки

(11)

и дисперсии оценки

. (12)

Оценка называется несмещённой, если среднее значение распределения равно измеряемому параметру . Тогда из (11) следует, что m_=. Оценка называется состоятельной, если она сходится по вероятности к оцениваемому параметру. При этом вероятность (Вер.) того, чтооценка даст результат, отличающийся от истинного значения , может быть сделана меньше любого 0, если число выборок n, на которых основана оценка, взять достаточно большим

, (13)

т.е. с увеличением числа выборок n распределение всё ”лучше концентрируется” вблизи истинного значения параметра (рис. 13).

Оценка является достаточной (использует достаточную статистику), если никакая другая оценка, вычисленная по той же выборке, не даёт дополнительной информации ^*).

Оценка называется эффективной, если среднее значение квадрата отклонения оценки от оцениваемого параметра (средний квадрат ошибки) не больше, чем средний квадрат любой другой оценки.

. (14)

Для несмещённых оценок средний квадрат ошибки равен дисперсии оценки. Тогда (14) эквивалентно

(15)

Относительная эффективность оценки ℓ(α) определяется

.

Для несмещённых оценок

. (17)

Метод максимального поавдоподобия наиболее широко используется в теории оценок. Для применения метода необходимо определить (задать) стати-стическое описание смеси сигнала и шума в виде условной плотности вероятности W(Y₁ ,Y₂ ,…Y_n/α), зависящей от измеряемого параметра сигнала α и принимаемой выборки Y₁ ,Y₂ ,…Y_n. Оценка параметра α определяется по функциональной зависимости условной плотности вероятности W(Y₁ ,Y₂ ,…Y_n/α) от измеряемого параметра α. Поскольку эта функциональная зависимость очень важна в задачах оценки (измерения), то распределение W(Y₁ ,Y₂ ,…Y_n/α), рассматриваемое как функция от α, получило специальное название – функция правдоподобия. В этом случае часто вводят даже специальное обозначение L_Y(α).

Метод максимального правдоподобия состоит в следующем. Наблюда- емые выборочные данные У^/T=(Y^/₁ ,Y^/₂ ,…Y^/_N) подставляются в выражение для условной плотности вероятности W(Y₁ ,Y₂ ,…Y_N/α). После подстановки эта плотность вероятности W(Y₁ ,Y₂ ,…Y_N/α) становится функцией одного параметра α - функцией правдоподобия . Функция дифференцируется для отыскания максимума. Значение параметра , при котором производная обращается в нуль, и представляет оценку по методу максимального правдоподобия

. (18)

На рис. 14 показан вид функции правдоподобия для двух значений выборочного вектора У^/T=(Y^/₁ ,Y^/₂ ,…Y^/_N) и У^//T=(Y^//₁ ,Y^//₂ ,…Y^//_N). Так как выборочные векторы У^/ и У^// случайны, то случайны и результаты измерений и , они отклонены от истинного значения параметра α_и. Оценки максимального правдоподобия обладают полезными свойствами:

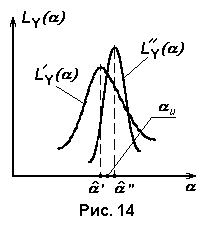
1. Они являются состоятельными.

2. Они асимптотически эффективны, т.е. среднеквадратическая ошибка стремится к минимально возможной, когда число выборок становится большим.

3. Распределение оценки асимптотически приближается к нормальному.

В другой форме (18) можно представить, используя тот факт, что для фиксированного значения выборки условная плотность вероятности W(Y₁ ,Y₂ ,…Y_N/0) при отсутствии сигнала принимает постоянное значение и не зависит от измеряемого параметра α. Тогда максимизация (18) эквивалентна максимизации отношения правдоподобия λ_Y(α), как функции измеряемого параметра

. (19)

Таким образом для отыскания оценки α необходимо установить функциональную зависимость отношения правдоподобия пачки импульсов от угловой координаты.