
сем 1 / лаба 3 физика ИССЛЕДОВАНИЕ ДИНАМИКИ КОЛЕБАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ (сем 1)
.docxОбработка результатов
1.Определим
по данным таблица значения времен tд
=
 ,
t0д
=
,
t0д
=
 ,
tк
=
,
tк
=
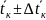 ,
t0к
=
,
t0к
=
 с P
= 95%:
с P
= 95%:
Упорядочим таблицу в порядке возрастания:
№ |
t д, с |
t 0д, с |
t к, с |
t 0к, с |
1 |
11,25 |
48,35 |
16,04 |
50,65 |
2 |
11,31 |
49,35 |
16,06 |
52,07 |
3 |
11,49 |
49,44 |
16,41 |
53,28 |
4 |
11,59 |
49,66 |
16,41 |
53,37 |
5 |
11,62 |
49,66 |
16,48 |
53,59 |
Rt д = t д max - t д min = 11,62 - 11,25 = 0,4 (с)
Rt 0д = t 0д max - t 0д min = 49,66 - 48,35 = 0,31 (с)
Rt к = t к max - t к min = 16,48 - 16,04 = 0,44 (с)
Rt0к = t 0к max - t 0к min = 53,59 - 50,65 = 2,94 (с)
Проверка на промахи:
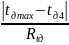 =0,075<
Up,N
=0,64 промаха нет
=0,075<
Up,N
=0,64 промаха нет
 =0,15<
Up,N
=0,64 промаха нет
=0,15<
Up,N
=0,64 промаха нет
 =0<
Up,N
=0,64 промаха нет
=0<
Up,N
=0,64 промаха нет
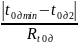 =3,22<
Up,N
=0,64 промах
=3,22<
Up,N
=0,64 промах
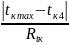 =0,16<
Up,N
=0,64 промаха нет
=0,16<
Up,N
=0,64 промаха нет
 =0,05<
Up,N
=0,64 промаха нет
=0,05<
Up,N
=0,64 промаха нет
 =0,07<
Up,N
=0,64 промаха нет
=0,07<
Up,N
=0,64 промаха нет
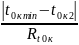 =0,48<
Up,N
=0,64 промаха нет
=0,48<
Up,N
=0,64 промаха нет
Рассчитываем
среднее значение по формуле

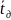 =11,45
(с)
=11,45
(с)
 =
49,29
(с)
=
49,29
(с)
 =16,28
(с)
=16,28
(с)
 =52,59
(с)
=52,59
(с)
Рассчитываем
СКО среднего по формуле
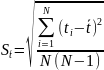
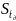 =
0,07
(с)
=
0,07
(с)
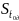 =
0,24
(с)
=
0,24
(с)
 =
0,09
(с)
=
0,09
(с)
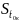 =
0,55
(с)
=
0,55
(с)
Расчет
случайной погрешности по формуле Δt
= tp,N
*
при N=5, tp,N =2,77, p=95%. Δtд = 0,19 (с)
Δt0д = 0,66 (с)
Δtк = 0,25 (с)
Δt0к = 1,52 (с)
Рассчитаем приборную погрешность,
Δ = 0,01 − цена деления секундомера ;
ΘT
=
 = 0,005
= 0,005
Найдём полную погрешность результата измерений.
Δ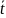 =
=
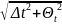
Δ д = 0,19 (с)
Δ 0д = 0,66 (с)
Δ к = 0,25 (с)
Δ 0к = 1,25 (с)
Запишем
результаты в стандартной форме: t
=

tд
=
11,45
 0,19
с
0,19
с
t0д = 49,29 0,66 с
tк = 16,28 0,25 с
tд = 52,59 1,25 с
2.Рассчитаем
периоды (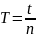 )
диска без кольца и с кольцом Tд
=
)
диска без кольца и с кольцом Tд
=
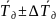 ,
Tк
=
,
Tк
=
 с P
= 95%:
с P
= 95%:
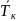 =
= =
= (с)
(с)
Вычисляем
частные производные от функции
=
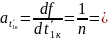 0,2
0,2
Вычисляем полную погрешность функции
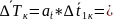 0,05
(с)
0,05
(с)
Запишем результат измерения и округлим его.
 (c)
(c)
 =
= =
=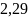 (с)
(с)
Вычисляем
частные производные от функции
=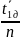
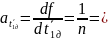 0,2
0,2
Вычисляем полную погрешность функции
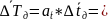 0,038
(с)
0,038
(с)
Запишем результат измерения и округлим его.
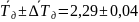 (с)
(с)
3.Рассчитаем
времена затухания (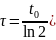 колебаний диска без кольца и с кольцом
τд
=
колебаний диска без кольца и с кольцом
τд
=
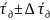 ,
τк
=
,
τк
=
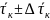 с P
= 95%.
с P
= 95%.
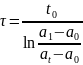
Рассчитываем
значение функции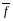 = f(
).
= f(
).
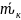 =
= =
= (с)
(с)
Вычисляем частную производные от функции
=
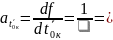 1,44
1,44
Вычисляем полную погрешность функции
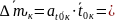 7,58
(с)
7,58
(с)
Запишем результат измерения и округлим его.
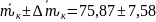 (с).
(с).
 =
= =
=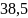 (с)
(с)
Вычисляем частную производную от функции
=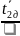
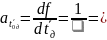 1,44
1,44
Вычисляем полную погрешность функции
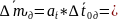 7,1
(с)
7,1
(с)
Запишем результат измерения и округлим его.
 (с)
(с)
4.Рассчитаем собственные частоты колебаний маятника без кольца и с кольцом
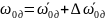 ,
,
 с Р=95%:
с Р=95%:
Рассчитываем значение функции = f( ).
 =
= =
=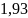 (рад/с)
(рад/с)
Вычисляем частные производные от функции
=
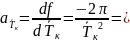 -0,5
-0,5
Вычисляем полную погрешность функции
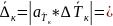 0,025
(рад/с)
0,025
(рад/с)
Запишем результат измерения и округлим его.
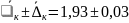 (рад/с).
(рад/с).
 =
=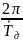 =
=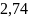 (рад/с)
(рад/с)
Вычисляем частные производные от функции
=
 -1,20
-1,20
Вычисляем полную погрешность функции
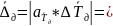 0,05(рад/с)
0,05(рад/с)
Запишем результат измерения и округлим его.
 (рад/с)
(рад/с)
Определим
собственные частоты
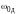 и
и
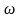 0к
колебаний для диска без кольца и с
кольцом:
0к
колебаний для диска без кольца и с
кольцом:
Рассчитываем
значение функции
= f( ).
).
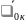 =
=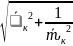 =
(рад/с)
=
(рад/с)
Вычисляем частные производные от функции
=
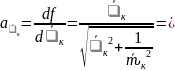 0,99
0,99
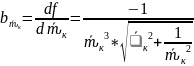 =
-1,19*10-6
=
-1,19*10-6
Вычисляем полную погрешность функции
 0,02
(рад/с)
0,02
(рад/с)
Запишем результат измерения и округлим его.
 (рад/с).
(рад/с).
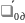 =
=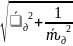 =
(рад/с)
=
(рад/с)
Вычисляем частные производные от функции
=
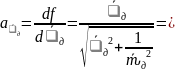 0,99
0,99
 =
-
6,35
∙ 10-6
=
-
6,35
∙ 10-6
Вычисляем полную погрешность функции
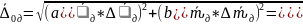
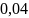 (рад/с)
(рад/с)
Запишем результат измерения и округлим его.
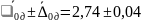 (рад/с)
(рад/с)
5.Используя
данные таблицы, рассчитаем момент
инерции кольца Iк
по
формулам
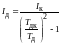 ,
,


6.Рассчитаем
момент инерции диска
 с P=95%:
с P=95%:
Пользуясь методом переноса погрешностей, рассчитаем Iд:
Рассчитываем
значение функции
= f(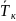 ,
,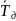 ).
).
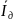 =
=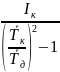 =
=
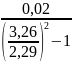 = 0,19 (кг*м2)
= 0,19 (кг*м2)
Вычисляем частные производные от функции
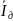 =
=
 -0,007
-0,007
 =
0,032
=
0,032
Вычисляем полную погрешность функции
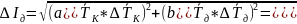 1,3*10-3
(кг*м2)
1,3*10-3
(кг*м2)
Записываем результат измерения и округляем его.
 (кг*м2)
(кг*м2)
7.Используя
данные таблицы рассчитаем значение
момента инерции диска маятника
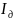 ,
исходя из его размеров и плотности
материала. Сравним полученный результат
с экспериментальным значением.
,
исходя из его размеров и плотности
материала. Сравним полученный результат
с экспериментальным значением.
Iд
=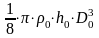 ,
где
,
где
 -
плотность материала, из которого
изготовлен диск; h0
– толщина диска маятника; D0
– диаметр диска маятника.
-
плотность материала, из которого
изготовлен диск; h0
– толщина диска маятника; D0
– диаметр диска маятника.
Iд=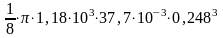 =
0,27
(кг*м2).
=
0,27
(кг*м2).
8.Найдем
коэффициент кручения
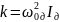 и, используя данные таблицы, значение
модуля сдвига G
и модуля Юнга E
материала
подвеса маятника.
и, используя данные таблицы, значение
модуля сдвига G
и модуля Юнга E
материала
подвеса маятника.
Рассчитываем
значение функции
= f(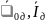 )
)
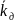 =
= =
=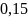 (рад*кг*м2)
(рад*кг*м2)
Вычисляем частные производные от функции
=
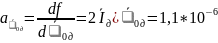
 =
7,5
=
7,5
Вычисляем полную погрешность функции
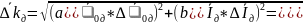 0,08
(рад*кг*м2)
0,08
(рад*кг*м2)
Запишем результат измерения и округлим его.
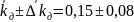 (рад*кг*м2)
(рад*кг*м2)
Рассчитаем среднее значение модуля сдвига G по формуле:
 ,где
l
– длина подвеса, d
– его диаметр, k
– коэффициент кручения.
,где
l
– длина подвеса, d
– его диаметр, k
– коэффициент кручения.
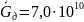 (Па)
(Па)
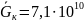 (Па)
(Па)
Е = 2G(1+v), где v коэффициент Пуассона – отношение поперечной и продольной относительной деформации образца материала и для металлов близок к 0.3
Е=18,2*1010 (Н/м2)
9.Определим
начальное значение полной энергии W0,
мощности потерь
 и добротности маятника Q:
и добротности маятника Q:
Определяем полную энергию

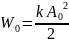
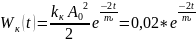 (Дж)
(Дж)
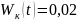 (Дж)
(Дж)
 (Дж)
(Дж)
 (Дж)
(Дж)
Определяем мощность потерь
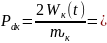 4*10-4
(Дж/с)
4*10-4
(Дж/с)
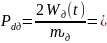 8,5*10-4
(Дж/с)
8,5*10-4
(Дж/с)
Определяем добротность маятника
 90
90
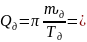 103
103
10. В соответствии с уравнением затухающих колебаний построим графики зависимости угла сдвига и амплитуды колебаний от времени для одного из наблюдений.
Построим графики для опыта с кольцом
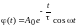

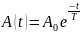
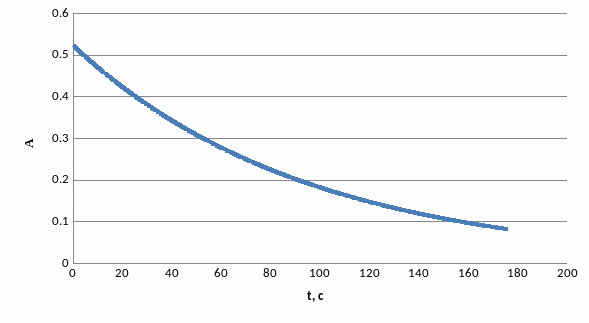
Вывод: Выполнив данную лабораторную работу, мы провели исследование динамики колебательного движения крутильного маятника. В процессе выполнения данной работы выяснилось, что колебательная система характеризуется достаточно малой потерей энергии и большой добротностью, что свидетельствует о хорошей способности системы сохранять энергию.
Теоретический и экспериментальный моменты инерции диска почти совпадают, небольшое расхождение в значениях моет быть связано с тем, что числа малы, а мы не учитываем все возможные погрешности.
Наш модуль Юнга почти совпадает с модулем Юнга меди, следовательно в нашем опыте маятник висел на медной проволоке.
