
сем 1 / лаба 10 ИССЛЕДОВАНИЕ ПРОЦЕССОВ ПЕРЕНОСА В ГАЗАХ (сем 1)
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра Физики
отчет
по лабораторной работе
по дисциплине «Физика»
Тема: ИССЛЕДОВАНИЕ ПРОЦЕССОВ ПЕРЕНОСА В ГАЗАХ
Студент гр. 3501 |
|
Сагандыкова А.А. |
Преподаватель |
|
Мыльников И.Л. |
Санкт-Петербург
2023
Цель работы.
Изучение явлений переноса в газе. Определение коэффициентов диффузии и вязкости воздуха, длины свободного пробега и эффективного диаметра его молекул.
Приборы и принадлежности.
Прибор для измерения объемной скорости истечения газа из трубки.
Основные теоретические положения.
Явления переноса. Хаотическое движение молекул в газе приводит к
тому, что в объеме газа поддерживается равновесное состояние, которое характеризуется постоянством его параметров состояния и концентрации молекул во всем объеме.
При
нарушении равновесия в газе хаотическое
движение молекул приводит к возникновению
макроскопических потоков, стремящихся
восстановить нарушенное равновесное
состояние. К явлениям переноса относят
диффузию, внутреннее трение (вязкость),
теплопроводность. Внутреннее трение –
это явление, обусловленное переносом
импульса молекул. Сила трения, возникающая
между слоями газа, определяется как
 ,
где
коэффициент внутреннего трения
(вязкости); v
скорость отдельных слоев газа;
,
где
коэффициент внутреннего трения
(вязкости); v
скорость отдельных слоев газа;

градиент скорости слоев газа в направлении,
перпендикулярном к поверхности,
разделяющей слои (в направлении оси z
перпендикулярной скорости слоев v); S
площадь соприкасающихся слоев.
градиент скорости слоев газа в направлении,
перпендикулярном к поверхности,
разделяющей слои (в направлении оси z
перпендикулярной скорости слоев v); S
площадь соприкасающихся слоев.
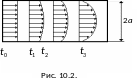
Течение газа в узкой цилиндрической трубке. Пусть газ течет в трубке с радиусом a и длиной l (l >> a) под действием разности давлений p на концах трубки (рис. 10.2).
В установившемся режиме (t > t3) изменение скорости течения газа по сечению трубки описывается параболической зависимостью
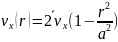
где r - расстояние, отсчитываемое от оси трубки,
 средняя по сечению
скорость течения газа (ось x
направлена по направлению скорости
слоев газа). Вблизи стенок трубки при r
= a
градиент скорости равен
средняя по сечению
скорость течения газа (ось x
направлена по направлению скорости
слоев газа). Вблизи стенок трубки при r
= a
градиент скорости равен
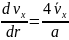
Учитывая, что сила
трения газа о стенки цилиндрической трубки
 ,
где Sб
2πal
площадь боковой поверхности трубки,
уравновешивает внешнюю силу, действующую
на газ в трубке, 2 F
pa2
, где Sс
a2
– площадь сечения трубки, получим
выражение для средней скорости слоев
газа:
,
где Sб
2πal
площадь боковой поверхности трубки,
уравновешивает внешнюю силу, действующую
на газ в трубке, 2 F
pa2
, где Sс
a2
– площадь сечения трубки, получим
выражение для средней скорости слоев
газа:
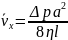 .
Это выражение называется формулой
Пуазейля. В данной работе измеряется
расход газа
.
Это выражение называется формулой
Пуазейля. В данной работе измеряется
расход газа
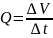 ,
определяемый как объем V
газа, вытекающий из трубки за некоторый
промежуток времени t.
Расход газа связан со средней скоростью
,
определяемый как объем V
газа, вытекающий из трубки за некоторый
промежуток времени t.
Расход газа связан со средней скоростью
 соотношением
соотношением
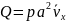 ,
так что средняя скорость слоев газа по
сечению трубки
,
так что средняя скорость слоев газа по
сечению трубки
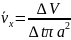 ,
приравнивая полученные выражения для
x v , получаем формулу для расчета
коэффициента вязкости газа:
,
приравнивая полученные выражения для
x v , получаем формулу для расчета
коэффициента вязкости газа:
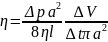 .
Диффузия
это явление, обусловленное переносом
массы молекул. Если различные области
занимаемого газом объема различаются
концентрацией молекул, то в газе возникают
макроскопические потоки молекул,
стремящиеся выровнять их концентрацию.
Процесс диффузии описывается законом
Фика:
.
Диффузия
это явление, обусловленное переносом
массы молекул. Если различные области
занимаемого газом объема различаются
концентрацией молекул, то в газе возникают
макроскопические потоки молекул,
стремящиеся выровнять их концентрацию.
Процесс диффузии описывается законом
Фика: ,
где m
масса газа, переносимая через площадь
поверхности S в единицу времени; D
коэффициент диффузии; d/dz
градиент плотности газа в направлении
переноса массы газа.
,
где m
масса газа, переносимая через площадь
поверхности S в единицу времени; D
коэффициент диффузии; d/dz
градиент плотности газа в направлении
переноса массы газа.
Контрольные вопросы:
1. Как вычисляются средняя, среднеквадратическая и наиболее вероятная скорости молекул газа?
Средняя скорость:

Подставляя
 и интегрируя, мы получим
и интегрируя, мы получим
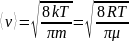
Среднеквадратичная скорость:
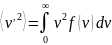
Подставляя и интегрируя, мы получим

Наиболее вероятная скорость:

где m – масса рассматриваемой частицы, μ – молярная масса.
2. Дайте определение коэффициента вязкости, коэффициента диффузии. Как они взаимосвязаны друг с другом?
Коэффициент вязкости есть физическая величина, численно равная силе внутреннего трения между двумя слоями с площадью, равной единице при поперечном градиенте скорости, равном единице.
Коэффициент диффузии – количественная характеристика скорости диффузии, равная количеству вещества, проходящего в единицу времени через участок единичной площади в результате теплового движения молекул при градиенте концентрации, равном единице.
Коэффициент диффузии и вязкость связаны уравнением Стокса-Эйнштейна.
Согласно уравнению Стокса-Эйнштейна, коэффициент трансляционной диффузии обратно пропорционален вязкости жидкости (при заданном молекулярном радиусе и температуре) Оба параметра играют решающую роль в таких процессах, как теплоперенос, массоперенос и гидродинамика.
Обработка результатов
2a, мм |
l, мм |
t1, °C |
T1, K |
p, Па |
0,8 |
250 |
25 |
298 |
99300 |
|
1 |
2 |
3 |
4 |
5 |
Δp, Па |
500 |
400 |
300 |
200 |
100 |
n0i, см |
5 |
5,7 |
6,7 |
7,4 |
8 |
ni, см |
5,5 |
6,2 |
7,2 |
7,9 |
8,5 |
Δti, с |
26,34 |
29,07 |
32,05 |
36,20 |
41,31 |


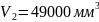




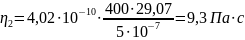

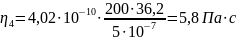

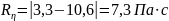
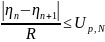
{0,2; 0,2; 0,3; 0,3;} ≤ 0,64 – промахов нет
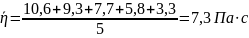
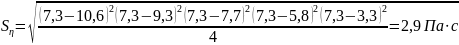

2.
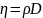


3.

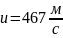
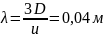
4.


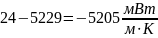
5.



Вывод: Полученные результаты прямо дают понять, что прибор неисправен, а вычисленные на нем показания разнятся с действительностью.

