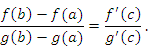20. Теорема Лагранжа.
Теорема. Пусть функция дифференцируема в открытом промежутке и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка , что
|
|
(13) |
|
Доказательство. Рассмотрим вспомогательную функцию
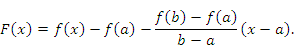
Эта функция непрерывна и дифференцируема в промежутке , а на его концах принимает одинаковые значения:
Тогда
удовлетворяет всем условиям теоремы
Ролля и, следовательно, существует точка
,
в которой производная функции
равна нулю:
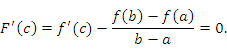
Следствие
1.
В частном случае, когда 
,
из теоремы Лагранжа вытекает, что
существует точка
,
в которой производная функции
равна
нулю: 
.
Это означает, что теорема Лагранжа
является обобщением теоремы
Ролля.
Следствие
2.
Если 
во всех точках некоторого промежутка
,
то
в
этом промежутке.
Действительно, пусть 
и 
– произвольные точки промежутка
и 
.
Применяя теорему Лагранжа к промежутку
,
получим
Однако во всех точках промежутка . Тогда
Учитывая
произвольность точек
и
,
получаем требуемое утверждение.
Геометрическая
интерпретация теоремы Лагранжа.
Разностное отношение в правой части
формулы (13) есть угловой коэффициент
секущей, проходящей через точки 
и 
,
а производная 
равна угловому коэффициенту касательной
к графику функции 
в некоторой средней точке промежутка
.
Поэтому за теоремой Лагранжа закрепилось
название “теорема о среднем”.
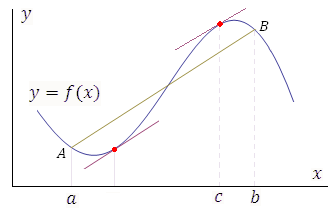Рис.
6.
Теорема Лагранжа устанавливает условия
существования хотя бы одной точки c,
в которой касательная к графику функции
параллельна секущей AB.
Таких точек может быть несколько.
Физическая
интерпретацию теоремы Лагранжа.
Пусть функция
описывает
смещение частицы из начального положения
в зависимости от времени x ее движения
по прямой. Тогда разностное отношение
представляет
собой среднюю скорость движения частицы
за промежуток времени 
,
а производная
– мгновенную скорость движения частицы
в момент времени c.
Существует такой момент времени, в
который мгновенная скорость движения
равна средней скорости.
Отметим, что формула (13) сохраняет свою
справедливость и при b < a.
Если применить теорему Лагранжа к
промежутку 
и представить значение c
в виде
где
то
формула (13) примет вид
|
|
(14) |
|
Равенство (14) дает точное значение для приращения функции при конечном значении приращения аргумента и называется формулой конечных приращений. Единственным недостатком этой замечательной формулы является присутствие в ней неопределенного числа θ.
21. Теорема Коши.
Теорема.
Пусть функции
и 
непрерывны в замкнутом промежутке
;
дифференцируемы в открытом промежутке
;
в открытом промежутке
.
Тогда существует такая точка
,
что
|
|
(15) |
|
Доказательство.
Заметим, что 
.
В противном случае – согласно теореме
Ролля – производная 
обратилась бы в нуль в некоторой точке
.
Рассмотрим вспомогательную функцию
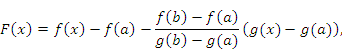
которая удовлетворяет всем условиям теоремы Ролля и, в частности, принимает одинаковые значения на концах промежутка :
Тогда существует точка , в которой
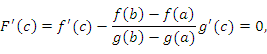
что
и требовалось доказать.
Следствие.
Теорема Лагранжа является частным
случаем теоремы Коши при 
.
В свою очередь теорема Ролля представляет
собой частный случай теоремы Лагранжа.
Таким образом, теорема Коши включает в
себя в качестве частных случаев теорему
Ролля и теорему Лагранжа.
22. Правило Лопиталя (формулировка).
23. Экстремумы функции одной переменной. Необходимое условие экстремума.
Вместе с 24
24. Экстремумы функции одной переменной. Достаточные условия экстремума.
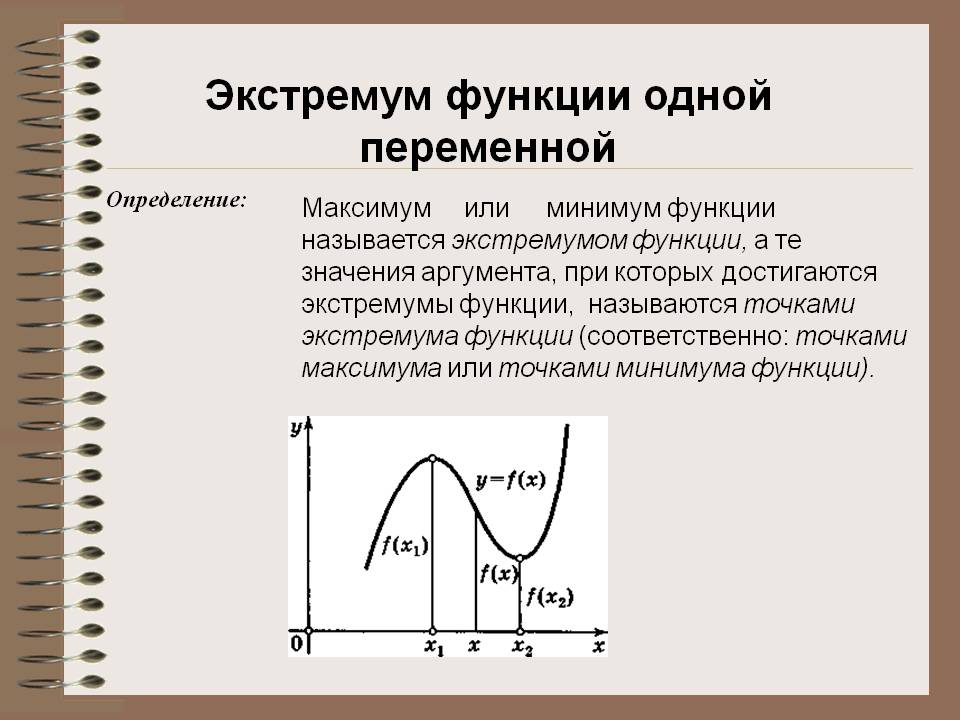
25. Направление выпуклости графика функции. Достаточное условие выпуклости графика
функции.
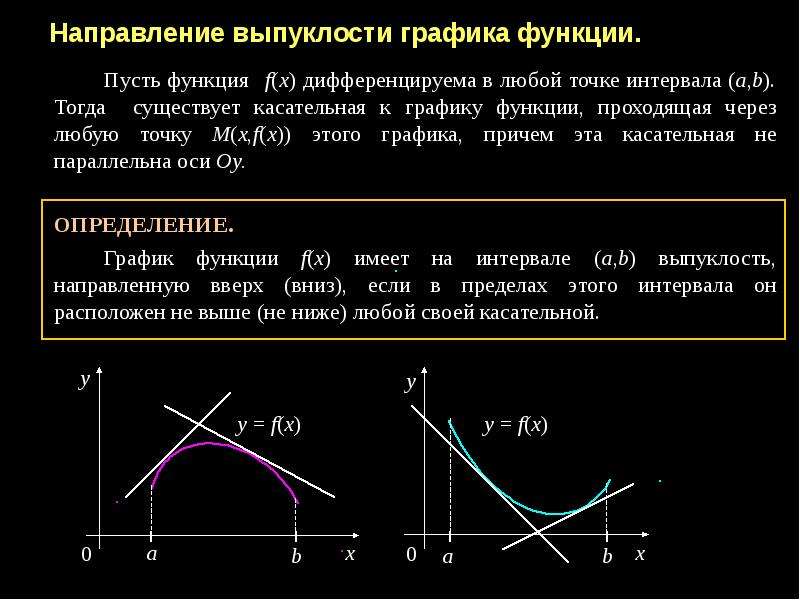
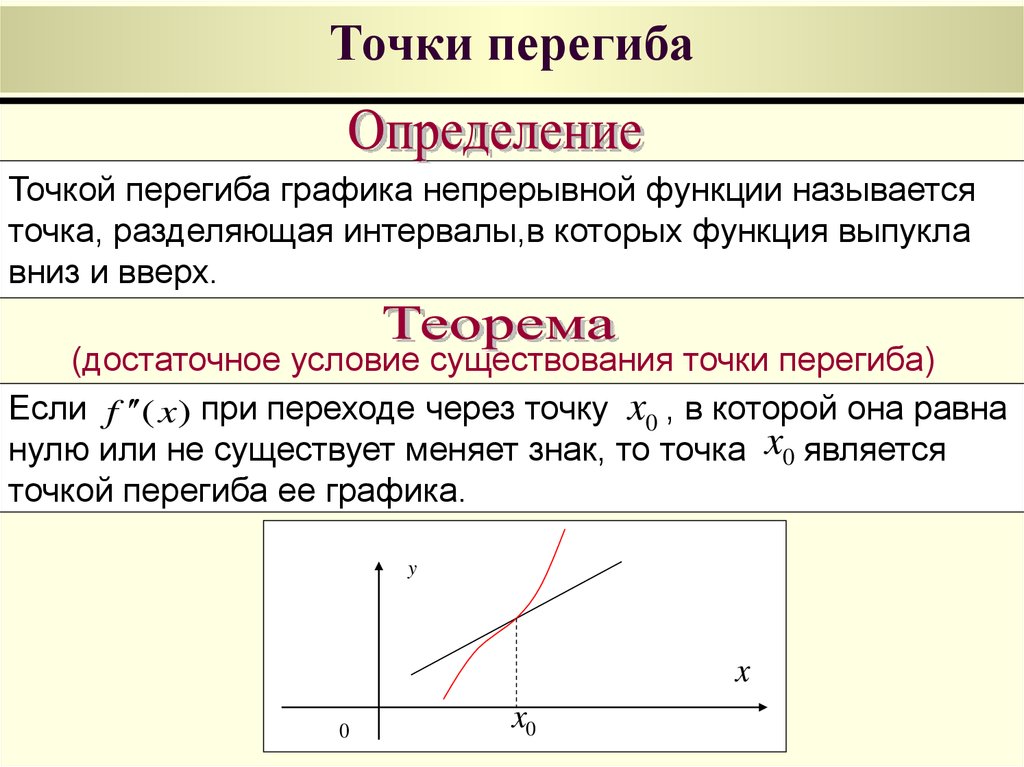
26. Точки перегиба. Необходимое условие существования перегиба. Достаточное условие су-
ществования перегиба.
27. Понятие о многочлене Тейлора. Формула Тейлора для функции одной переменной (без доказательства). Формула Маклорена для функций e*, sin x, cos x.
28. Первообразная и неопределенный интеграл. Их свойства.
29. Первообразная и неопределенный интеграл. Методы вычисления неопределенных интегралов: интегрирование по частям и замена переменной.
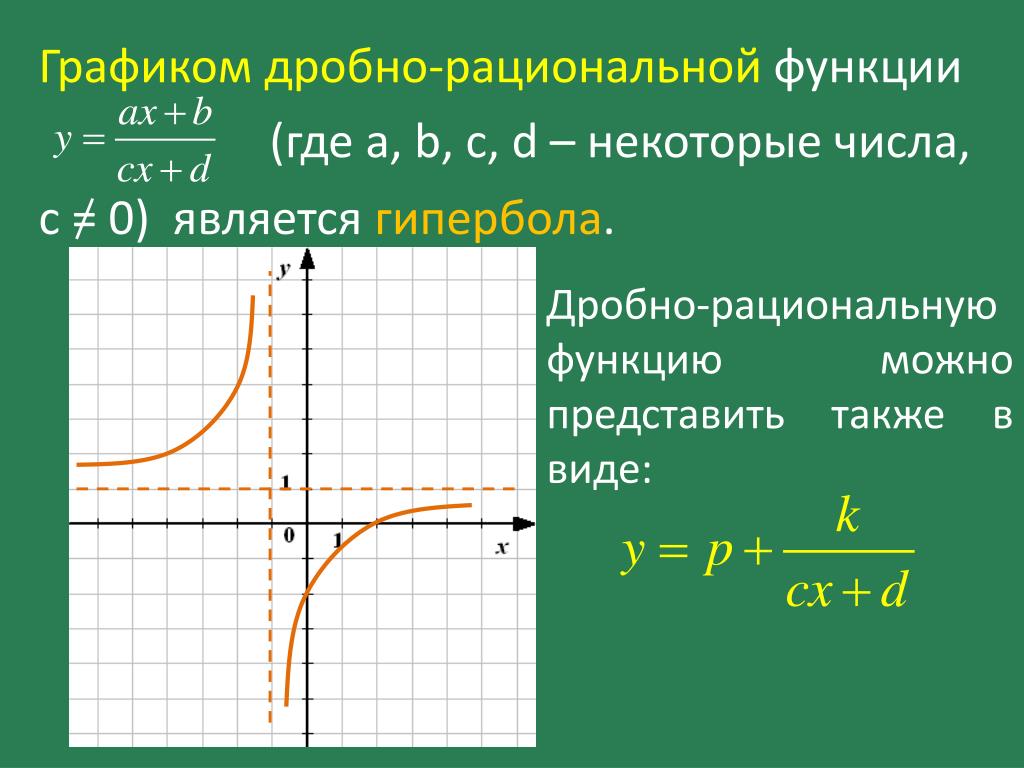
30. Дробно-рациональная функция. Типы простейших алгебраических дробей и их интегрирование.
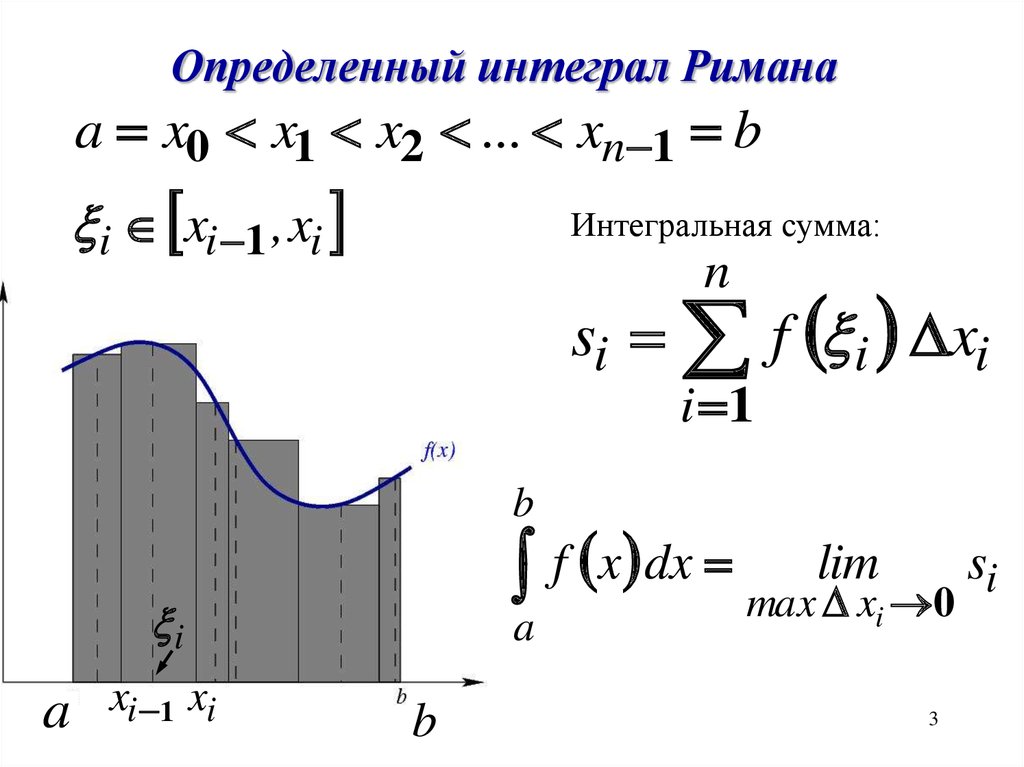
31. Интегральная сумма Римана. Определенный интеграл Римана. Интегрируемые функции.
Геометрическая интерпретация определенного интеграла.
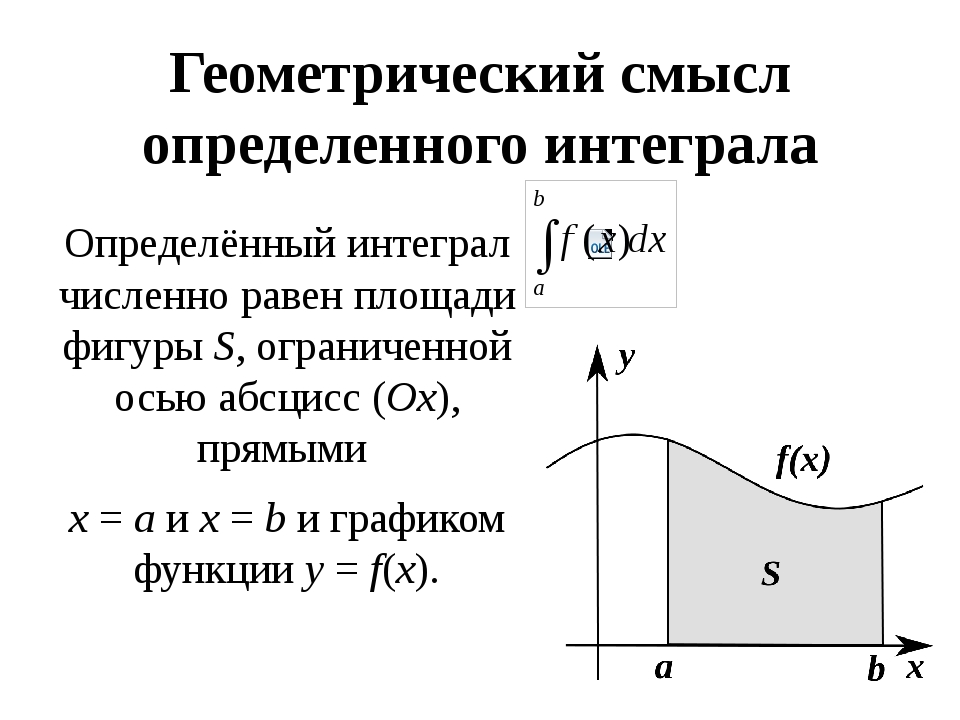
32. Определенный интеграл Римана. Свойства определенного интеграла. Теорема о среднем.
33. Определенный интеграл с переменным верхним пределом. Теорема о его производной.
Существование первообразной непрерывной функции.
34. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. И
И вопрос 33
35. Определенный интеграл Римана. Методы вычисления: интегрирование по частям и замена переменной.
36.
Понятие
о несобственных интегралах I-го
рода.
Интегралы вида
37.
Понятие
о несобственных интегралах II-го
рода.
Интегралы вида
38. Кривые на плоскости и в пространстве. Спрямляемая кривая, длина дуги кривой (вывод
формулы для явно заданной кривой). Дифференциал длины дуги.
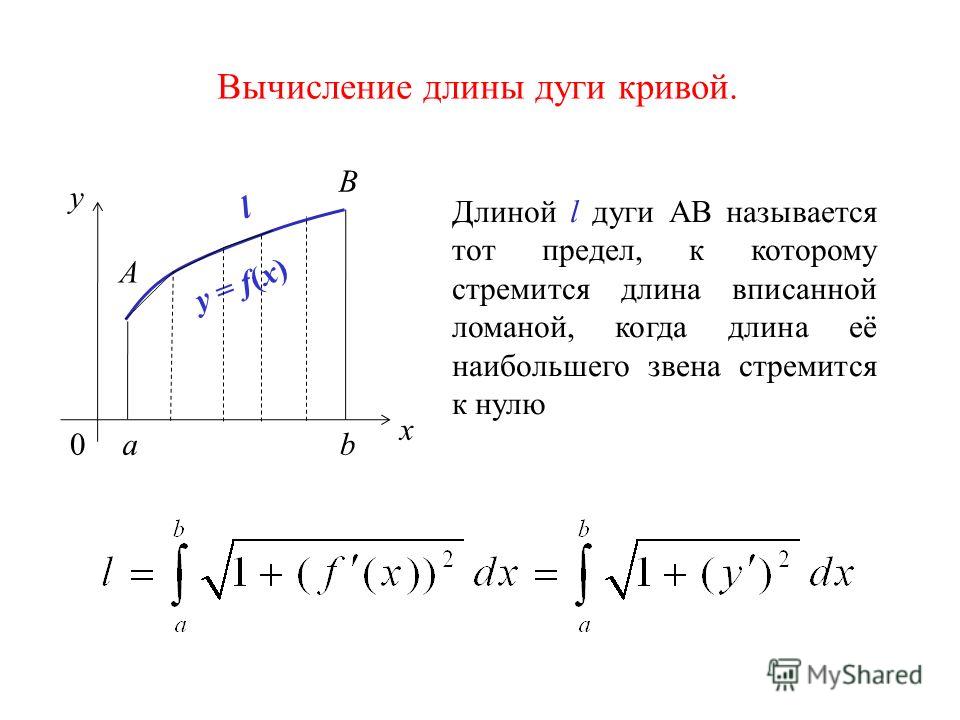
39. Вычисление площадей плоских фигур в декартовых и полярных координатах.
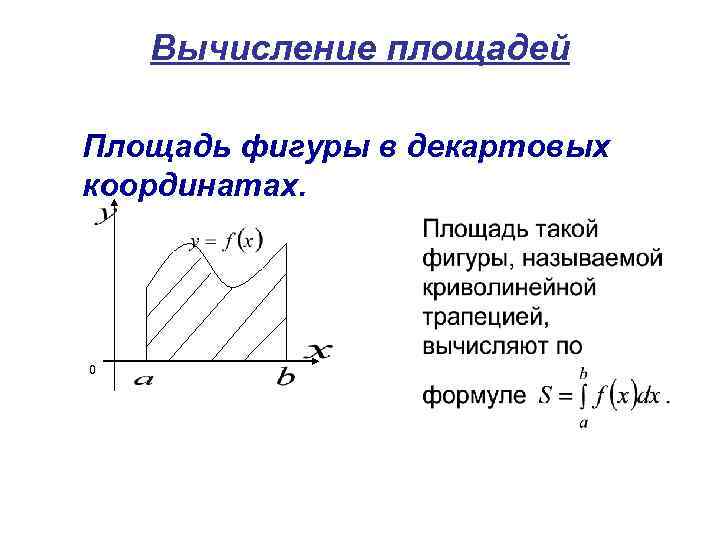
40. Вычисление объемов тел по площадям поперечных сечений и объемов тел вращения.
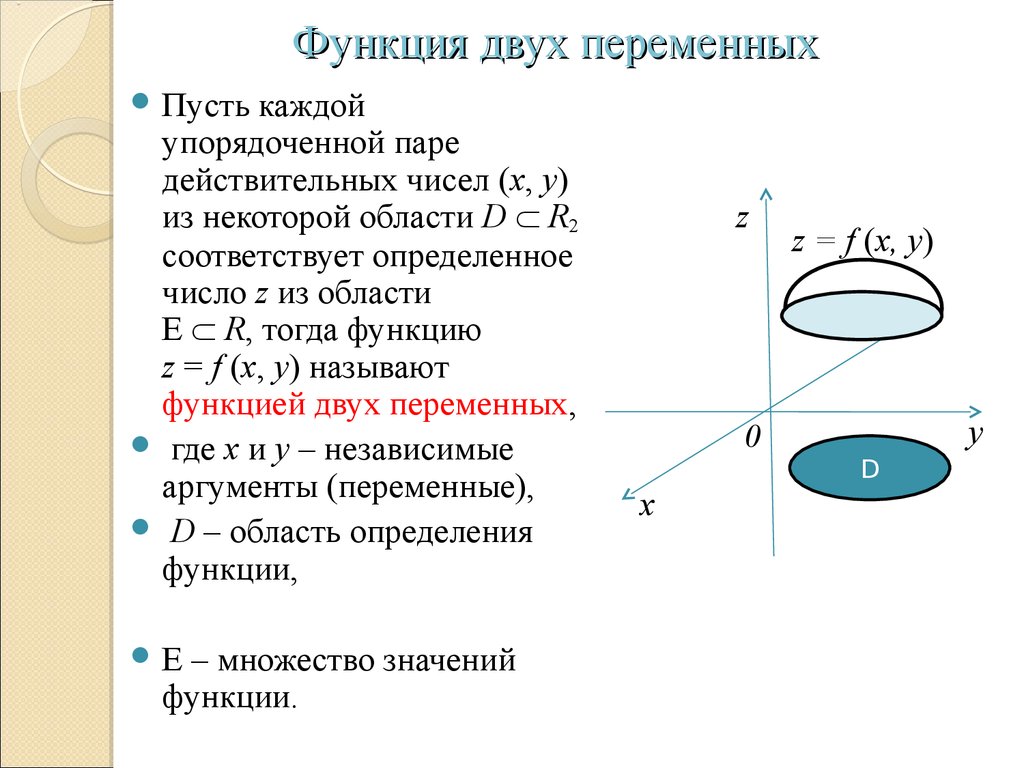
41. Функции двух переменных. Передел и непрерывность. Частные производные, их геометрическая интерпретация.
42. Дифференцируемые функции двух переменных. Полный дифференциал. Необходимое
условие дифференцируемости. Достаточное условие дифференцируемости.
43. Дифференцируемые функции двух переменных. Дифференцирование сложной функции.
44. Частные производные и дифференциалы высших порядков функции двух переменных.
Теорема о перестановке порядка дифференцирования (формулировка).
45. Формула Тейлора для функции двух переменных.
46. Экстремумы функции двух переменных. Необходимое условие существования экстремума.
В 47
47. Экстремумы функции двух переменных. Достаточное условие существования экстремума
(формулировка).
48. Дифференцирование функции, заданной неявно.
49. Определение двойного интеграла.
50. Вычисление двойного интеграла в декартовой системе координат.
Вычисление двойного интеграла сводится к вычислению двух определенных интегралов следующим способом.
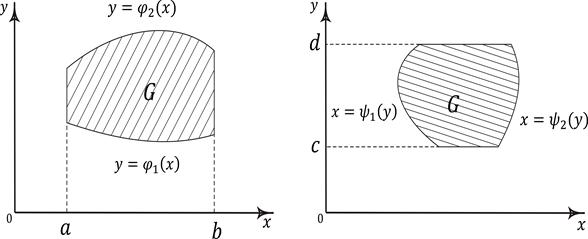
Пусть область G (рис. 6.3) ограничена кривыми
причем всюду
на отрезке 
функции 
и 
непрерывны
и 
.
Тогда
,
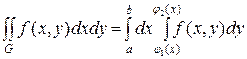причем сначала вычисляется внутренний определенный интеграл по переменной y, а полученный результат интегрируется во внешнем определенном интеграле по переменной x. При этом интеграл, стоящий в правой части формулы, называют повторным или двукратным интегралом.
Аналогично, если область G (рис. 6.3) ограничена кривыми
,
причем всюду
на отрезке 
функции 
и 
непрерывны
и 
,
то
,
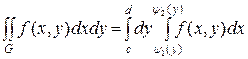причем сначала вычисляется внутренний определенный интеграл по переменной x, а полученный результат интегрируется во внешнем определенном интеграле по переменной y.
51. Вычисление двойного интеграла в полярной системе координат.
52. Приложения двойного интеграла.
53. Определение тройного интеграла.
54. Вычисление тройного интеграла в декартовой системе координат.
55. Вычисление тройного интеграла в цилиндрической системе координат.
56. Вычисление тройного интеграла в сферической системе координат.
57. Приложения тройного интеграла.
