1. Окрестность точки на числовой прямой. Предел функции в точке. Предел в бесконечно удаленной точке. Геометрическая интерпретация предела.

Пусть    произвольное фиксированное число.

Окрестностью точки    на числовой прямой (  -окрестностью) - множество точек, удаленных от x₀ не более чем на    →  .

В многомерном случае роль окрестности выполняет открытый   -шар с центром в точке x₀  .

2) Пусть задано некоторое числовое множество   и каждому   поставлено в соответствие число   , тогда на множестве   задана функция   ,   .

Число   - предел функции в точке a , если для     такое, что для   из того, что   →, что   :   или   при   .

3) Переменная x стремится к бесконечности, если для каждого заранее заданного положительного числа M можно указать такое значение х=х₀, начиная с которого, все последующие значения переменной будут удовлетворять неравенству |x|>M.

Например, пусть переменная х принимает значения x₁= –1, x₂=2, x₃= –3, …, x_n=(–1)ⁿn, … 

Бесконечно большая переменная величина, так как при всех M > 0 все значения переменной, начиная с некоторого, по абсолютной величине будут больше M.

Переменная величина x → +∞, если при произвольном M > 0 все последующие значения переменной, начиная с некоторого, удовлетворяют неравенству x > M.

Аналогично, x → – ∞, если при любом M > 0 x < -M.

Функция f(x) стремится к пределу b при x → ∞, если для произвольного малого положительного числа ε можно указать такое положительное число M, что для всех значений x, удовлетворяющих неравенству |x|>M, выполняется неравенство |f(x) - b| < ε.

Обозначают 

4) Если переменная x_n имеет пределом число a, то это значит, что как бы мало не было любое наперед заданное положительное число e, всегда можно найти такое значение x_N, что все последующие ее значения будут удовлетворять неравенству |x_n - a| < e при n і N (1)

Неравенство (1) равносильно следующим двум неравенствам:

-e < x_n - a < e (2)

Если x_n - a > 0,

то x_n - a < e

|x_n - a| < e

Если x_n - a < 0,

то -e < x_n - a 

|x_n - a| < e. Прибавляя a ко всем частям неравенств (2), получаем два других неравенства, равносильных неравенству (1)

2. Односторонние пределы. Теорема о существовании предела функции в точке.

Односторонний предел – предел числовой функции, подразумевающий приближение к предельной точке, с одной стороны. Такие пределы называют соответственно левым и правым.

Теорема (теорема "о двух милиционерах") Пусть даны три функции  f₁(x), f₂(x) и   , при всех   из некоторого окончания   базы   связанные неравенством

Пусть функции  f₁(x) и f₂(x) имеют общий предел при базе   :

Тогда функция   также имеет предел при базе   , равный тому же числу   :

Доказательство. Согласно определению предела, для любого   найдутся такие окончания базы E₁ и  E₂, что при   выполняется неравенство а при   -- неравенство

Значит, для окончания   при всех   выполняются неравенства

то есть

Это означает, что предел величины   равен L.

Рис.2.21.Два милиционера f₁и f₂ и пьяный   движутся в участок

3. Предел функции в точке. Теорема об единственности предела.

Пусть функция y=f(x) задана в некоторой окрестности точки х₀, кроме, быть может, самой точки х₀.

Число А называется пределом функции y=f(x) при х, стремящемся к х₀ (или в точке х₀), если для любого, даже сколь угодно малого положительного числа >0, найдется такое положительное число δ>0 (зависящее от , δ=δ(ɛ)), что для всех х, не равных х₀ и удовлетворяющих условию |х – х₀| < δ, выполняется неравенство |f(x) – A| < .

(A = lim _x → xо f(x))  ( > 0) ( δ = δ(ɛ) > 0) ( x ≠ x₀: |x – x₀| < δ): |f(x) – A| < .

Число А есть предел функции f(x) при х→х₀, если для любого ɛ>0 найдется такая δ-окрестность точки х0, что для всех х≠х₀ из этой окрестности соответствующие координаты графика функции f(x) будут заключены в полосе А-ɛ<y<A+ɛ, какой бы узкой эта полоса не была.

Смысл определения предела функции f(x) в точке х₀ состоит в том, что для всех значений х, достаточно близких к х₀, значения функции f(x) как угодно мало отличаются от числа А (по абсолютной величине).

Единственность предела: Функция не может иметь более одного предела.

Доказательство:

+Предположим противное, т.е. что функция f(x) имеет два предела А и D, А≠D. Тогда на основании теоремы о связи бесконечно малых величин с пределами функции f(x)=A+α(x), f(x)=D+β(x), где α(x) и β(x) – бесконечно малые при х→х₀. Вычитая почленно эти равенства, получим 0=A-D+(α(x)-β(x)), откуда α(x)-β(x)=D-A. Это равенство невозможно, т.к. на основании свойств бесконечно малых функций α(x)-β(x) есть величина бесконечно малая. Следовательно, предположение о существовании второго предела неверно.

4. Числовая последовательность. Предел числовой последовательности. Теорема о существовании предела монотонной ограниченной последовательности. Число е. 2-й «замечательный» предел.

5. Предел функции в точке. Теоремы о сохранении знака функции и о переходе к пределу в

неравенствах.

6. Бесконечно малые функции в точке. Теоремы о бесконечно малых.

7. Сравнение бесконечно малых. Эквивалентные бесконечно малые.

8. Теорема о связи функции, имеющей конечный предел с бесконечно малой. Теоремы об

арифметических операциях над пределами.

9. Теорема о сжатой переменной. 1-й «замечательный» предел.

10. Непрерывность функции в точке. Точки разрыва. Классификация точек разрыва.

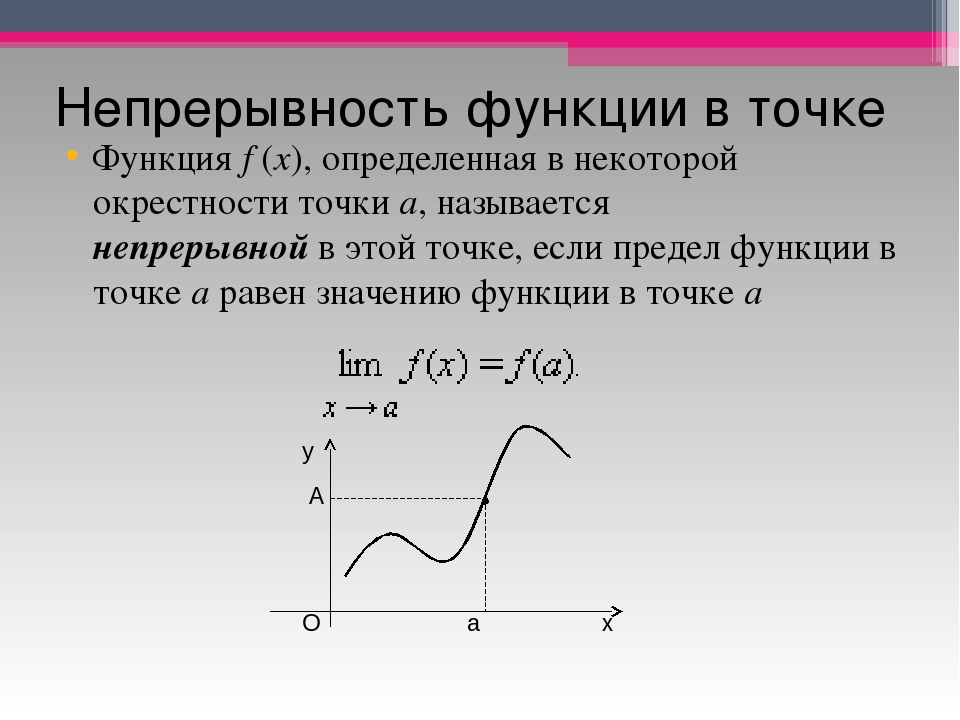
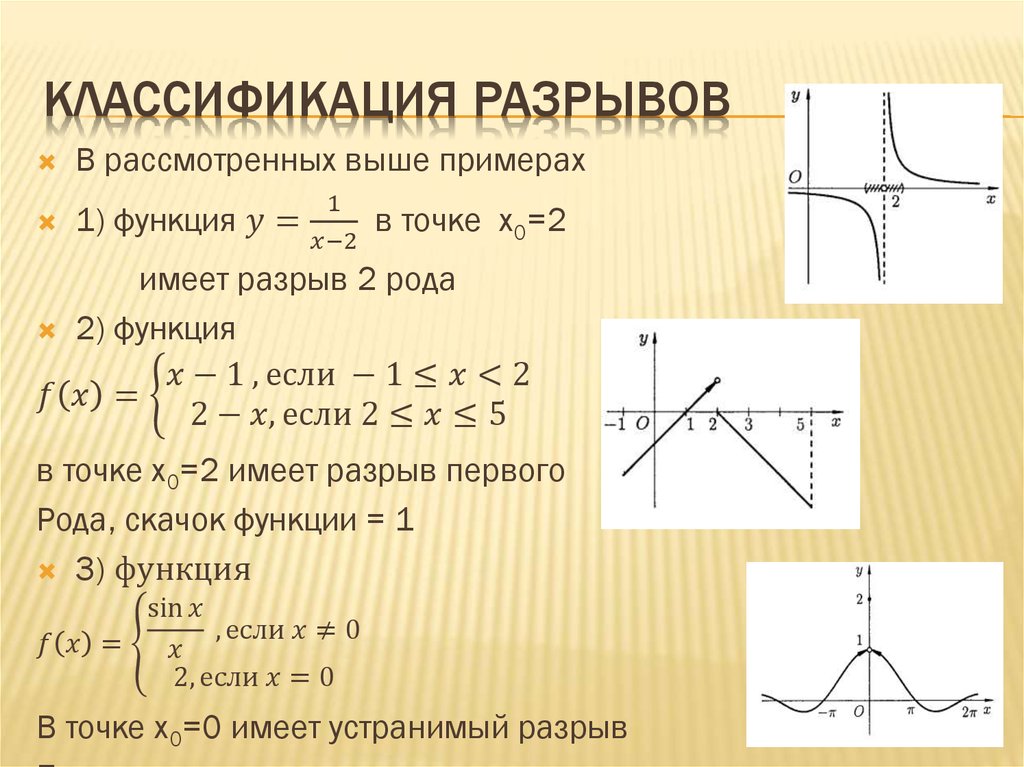
11. Непрерывность функции в точке и на отрезке. Теоремы Коши (без док-ва). Теоремы Вейерштрасса (без док-ва).

12. Производная функция в точке. Геометрическая и механическая интерпретация. Уравнение

касательной.

13. Дифференцируемые функции. Необходимое и достаточное условия дифференцируемости.

14. Производная функции в точке. Дифференцируемые функции. Непреерывность дифференцируемой функции.

15. Производная функции в точке. Правила дифференцирования суммы, произведения и

частного.

16. Производная функции в точке. Правила дифференцирования сложной и обратной функции.

17. Производные и дифференциалы высших порядков.

18. Теорема Ферма.

19. Теорема Ролля.

Теорема. Пусть функция     дифференцируема в открытом промежутке , на концах этого промежутка сохраняет непрерывность и принимает одинаковые значения:   . Тогда существует точка  , в которой производная функции     равна нулю:   .

Рис. 3. Теорема Ролля устанавливает условия существования хотя бы одной точки  c, в которой касательная к графику функции параллельна оси 0x. Таких точек может быть несколько.

      Доказательство. Если     в промежутке   , то     во всех точках этого промежутка. Иначе наибольшее значение  M  функции     превышает ее наименьшее значение  m  в промежутке   . Поскольку на концах этого промежутка функция     принимает одинаковые значения, то по крайней мере одно из значений,  M  или  m, достигается во внутренней точке  c  промежутка   . Тогда по теореме Ферма   . Физическая интерпретация теоремы Ролля. Пусть функция     описывает смещение частицы из начального положения     в зависимости от времени x ее движения по прямой. Тогда производная       представляет собой мгновенную скорость движения частицы в момент времени c. Возвращение частицы в исходное положение возможно только при ее остановке в некоторый момент и перемещении в обратном направлении.