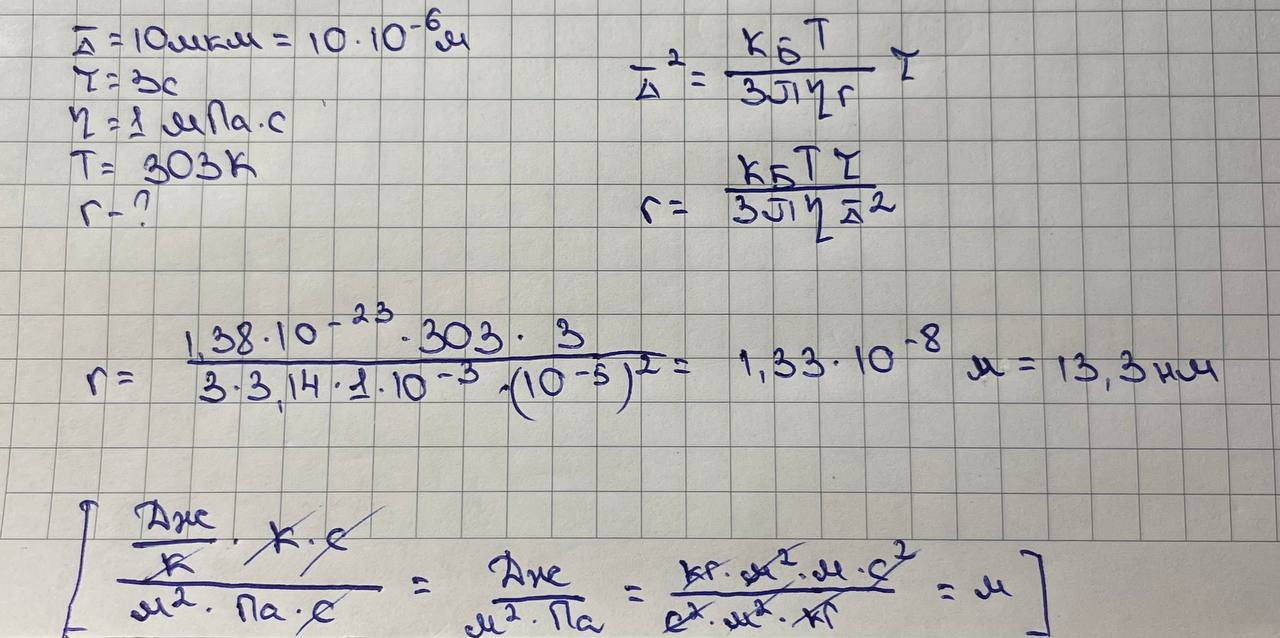Вариант 4 (их три, спроси какой)

номер 1

1. Приведите графический вид интегральной и дифференциальной кривых распределений объёма пор по радиусу? Каково назначение этих кривых?

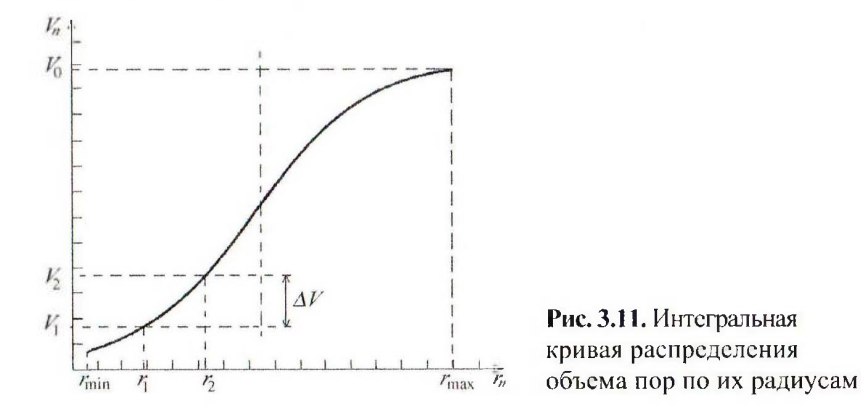
Как объяснить график: Ось y это Vп, ось x это rп ближе к концу осей отмечаешь Vo и rmax, от этих точек проводишь пунктиры так, чтобы образовался квадрат вместе с осями Чуть выше точки 0,0 начинаешь вести возрастающую кривую, которая сначала создает вогнутость, а затем выпуклость Точку начала кривой на оси x отмечаешь rmin и поднимаешь к ней пунктир от оси x, на этой же оси чуть дальше отмечаешь r1 и еще дальше r2, от них также проводишь пунктиры до пересечения с кривой, на оси y отмечаешь V1 и V2 (эти точки получаем путем проведения пунктира от точки пересечения предыдущих пунктиров проведенных от r1 и r2). Расстояние между V1 и V2 отмечаешь ΔV

Каждая отдельная точка на этой кривой дает объем пор (например, V1) с радиусами от минимально rmin до данного (например, r1). Отсюда следует, что ΔV = V2 - V1 представляет собой объем пор с радиусами от r1 до r2. Если общий объем пор принять равным Vо, то можно рассчитать долю объема (в процентах), которая принадлежат порам с радиусами от r1 и до r2: (ΔV/ Vо)100%.

Показывает какой объем приходится на поры интересующего размера

Дифференцируя, тем или иным способом, интегральную кривую по радиусам пор, получают дифференциальную кривую распределения объема пор по их радиусам. Максимум на этой кривой должен соответствовать положению точки перегиба на интегральной кривой.

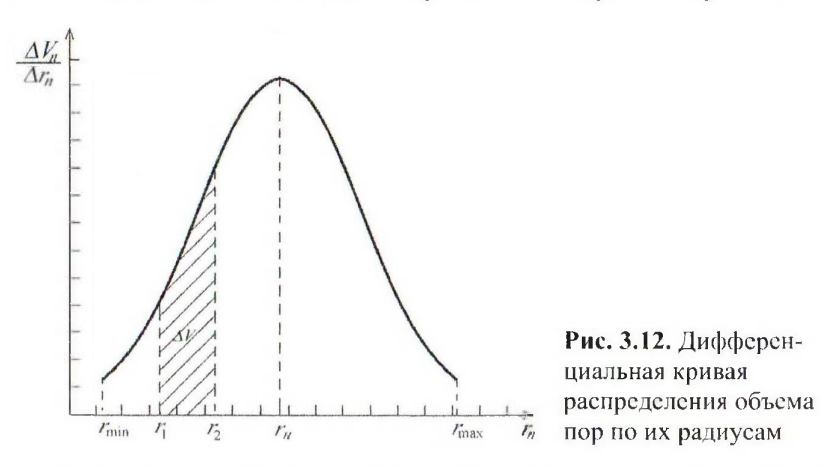
Ось y это ΔVп/Δrп, ось x это rп ближе к концу оси x отмечаешь rmax

Чуть выше точки 0,0 начинаешь вести возрастающую кривую, которая доходит до максимального значения и начинает убывать, формируется выпуклый симметричный пик Точку начала кривой на оси x отмечаешь rmin и поднимаешь к ней пунктир от оси x, на этой же оси чуть дальше отмечаешь r1 и еще дальше r2, от них также проводишь пунктиры до пересечения с кривой, расстояние между ними штрихуешь и отмечаешь ΔV, от центра оси x к центру пика проводишь пунктир и отмечаешь точку rн

Радиус, соответствующий максимуму на дифференциальной кривой, называют наивероятнейшим радиусом, так как пор с таким радиусом в адсорбенте больше всего (их вклад в суммарный объем пор максимален). Этот радиус также может выступать в качестве характеристики дисперсности пор адсорбента

Показывает каких пор с каким радиусом в адсорбенте больше

номер 2

2. Напишите формулу мицеллы гидрозоля йодида серебра, образующегося при смешивании водных растворов KI и AgNO3, причём количество молей KI избыточное. Сформулируйте правила Фаянса-Панета.

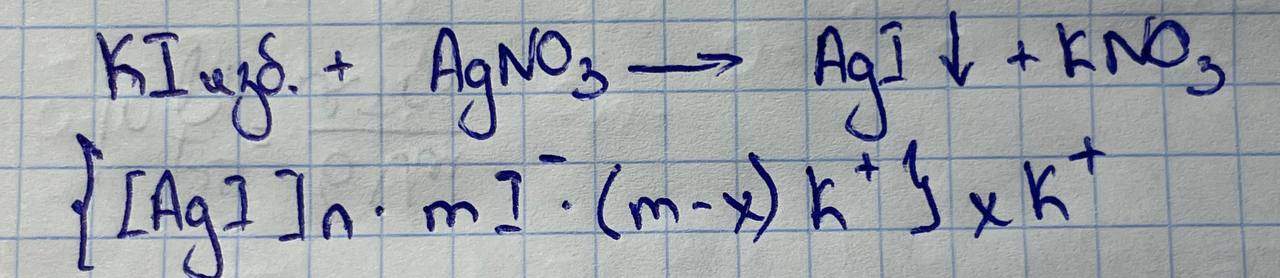
где n - число молекул в кристалле (агрегате); m - число потенциалопределяющих ионов; (m — х) — число противоионов в слое Гельмгольца; х - число ионов в диффузном слое

В соответствии с правилом Фаянса - Панета структуру кристаллической решетки могут достраивать только те ионы, которые входят в ее состав.

номер 3

3. Используя уравнение седиментационно-диффузионного равновесия (гипсометрический закон), рассчитайте высоту, на которой концентрация частиц Al2O3 с радиусом 12 нм будет вдвое меньше, чем у сосуда. Температура 20C, плотность частиц 4,0 г/см3, плотность операционной среды 1 г/см3.

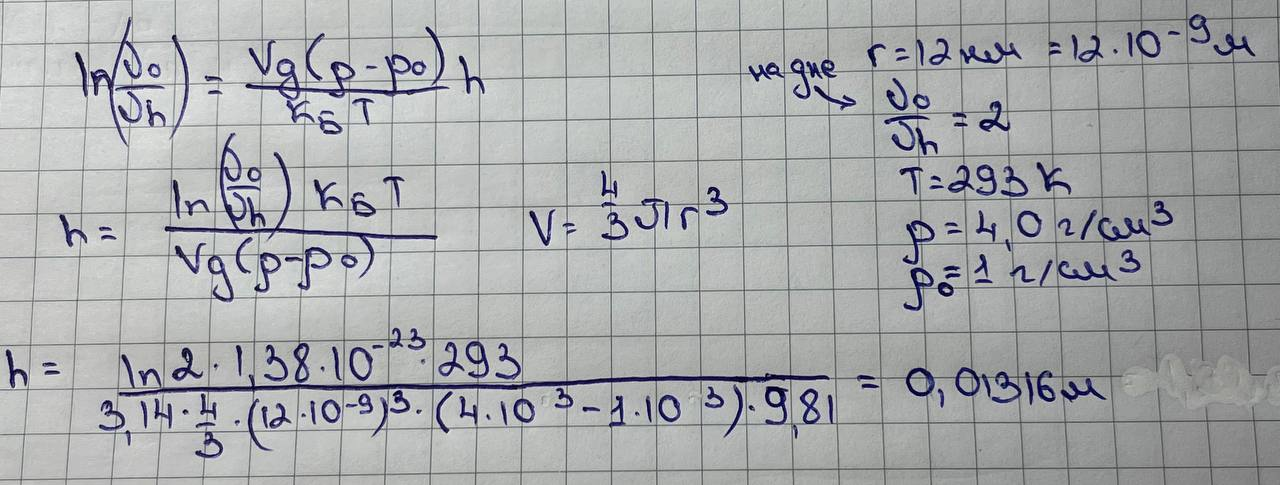
номер 4

4. Среднеквадратичное значение проекции смещения частиц гидрозоля металлического серебра в воде за 3 секунды составляет 10 мкм. Рассчитайте радиус частиц, если вязкой среды равна 1 мПа*с при температуре 30С.