Вариант 2 (их три, спроси какой)

номер 1

1. Какие уравнения описывают зависимость натяжения растворов ПАВ от их концентрации? При каких условиях они применимы? Каков физический смысл констант этих уравнении?

Область высоких концентраций

Как описать график:

Ось y это A/сигма, ось x это с.

Из точки 0,0 проводишь возрастающую кривую, создающую выпуклость обозначаешь ее буквой A

На оси y ближе к верху отметить точку сигма0, из нее проводишь убывающую кривую, создающую вогнутость, счтобы получилось пересечения прямых крестом, эту кривую обозначить сигма

изотерма адсорбции описывается уравнением Ленгмюра , но еще соблюдается и уравнение Гиббса . Приравниваем правые части этих двух уравнений (без учета коэффициентов активности):

Далее делим переменные и интегрируем в техизотерма ад же пределах, что и в предыдущем случае:

После интегрирования получаем уравнение, известное под названием уравнения Шишковского:

Область низких концентраций

Как описать график:

Ось y это A/сигма, ось x это с.

Из точки 0,0 проводишь возрастающую прямую, обозначаешь ее буквой A

На оси y ближе к верху отметить точку сигма0, из нее проводишь убывающую прямую, чтобы получилось пересечения прямых крестом, эту прямую обозначить сигма

изотерма адсорбции описывается уравнением Генри , с другой стороны, в этом случае может быть использовано и уравнение Гиббса . Учитывая, что в рассматриваемых условиях , мы можем приравнять правые части этих уравнений:

Делим переменные и интегрируем при изменении концентрации ПАВ от нуля (чистый растворитель) до с. При этом поверхностное натяжение раствора меняется от σ0 до σ:

После интегрирования получаем уравнение, описывающее зависимость поверхностного натяжения разбавленного раствора от концентрации ПАВ: Поверхностное натяжение линейно зависит от концентрации ПАВ для случая адсорбции неионного ПАВ Поскольку при Kc<<1, In (1 + Кс) ~ Кс, то очевидно, что при низких концентрациях ПАВ уравнение Шишковского переходит в уравнение , так как

номер 2

2. При каких условиях возникает седиментационно-диффузионное равновесие? Как изменяется гипсометрическая высота, если размер частиц уменьшится в два раза (при прочих равных условиях)?

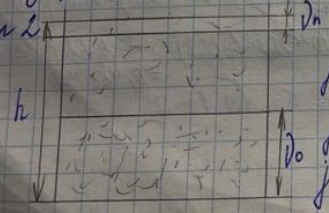
Как описать рисунок:

Рисуешь прямоугольник, проводишь линию параллельную дну прямоугольника с отступом от нее ⅔ прямоугольника, расстояние между ними отмечешь как ню0 и еще одну линию параллельную верху прямоугольника с отступом от него в 1 клетку ~ , расстояние между ними отмечешь как нюП, расстояние от верха до дна отмечаешь h

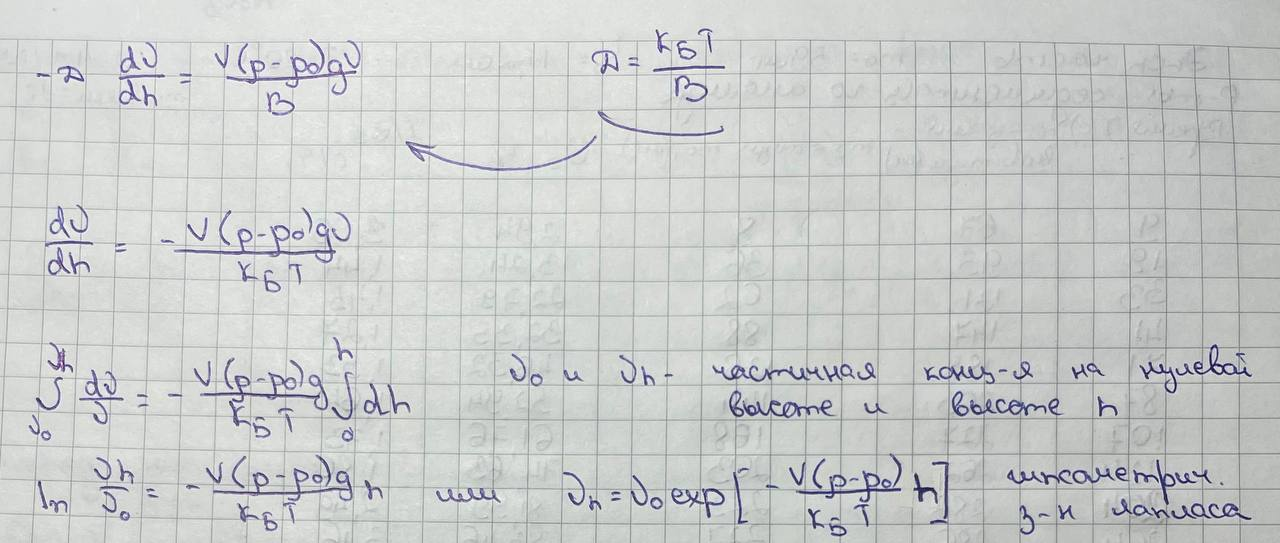
Если =1, то he гипсометрическая высота

Высота гипсометрическая - высота, на которой частичная концентрация в дисперсной системе уменьшается в е раз (является мерой термодинамической седиментационной устойчивости системы).

Vсф.частиц=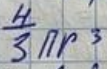

если уменьшить размер частиц в 2 раза, то V уменьшится в 8 раз, отсюда следует, что he увеличится в 8 раз

номер 3

3. Рассчитайте и постройте интегральную кривую распределения объема пор адсорбента по размерам, используя данные капиллярные конденсации метанола на силикагеле при 293 К (таблица) Плотность метанола ρ = 0,788 г/см3, поверхностное натяжение σ = 22,6 мДж/м2.

Интегральная кривая распределения объема пор по размерам:

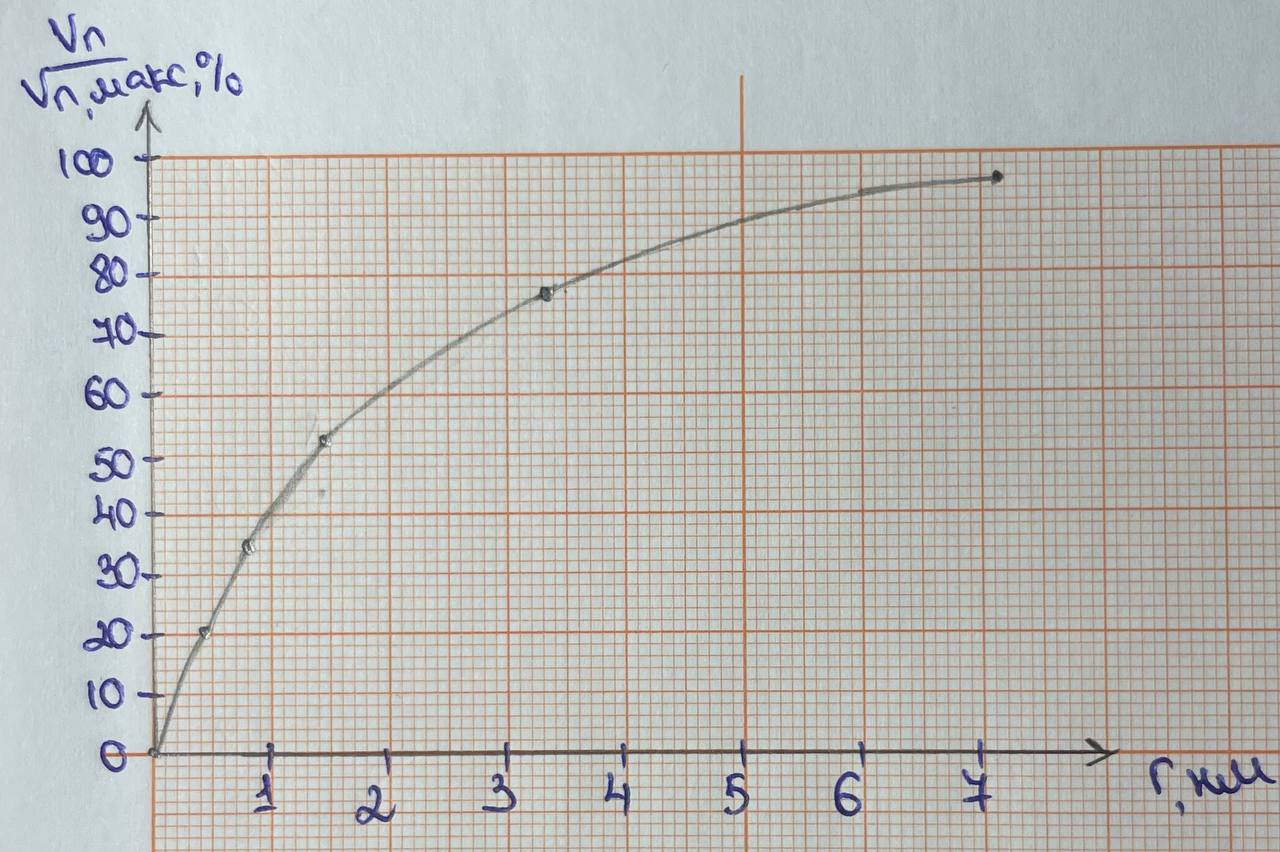
Как объяснить график:

Ось x это r, нм, ось y это ось Vп/Vп,max,%

Должна получиться возрастающая кривая, создающая выпуклость

По оси x взять шаг 1=1 полная клетка, по оси y взять шаг 10=половина полной клетки

номер 4

4. Электрофорез дисперсия бентонитовой глины происходил при следующих условиях: расстояние между электродами составляло 0,25 м, напряжение V = 100 В; за 15 минут границы переместились на 6 мм к аноду. Рассчитайте ?-потенциал частиц, если ε = 80,1, η = 1 мПа*с