Вариант 7 (их четыре, спроси какой)

номер 1

1. Как по по результатам адсорбции определить общий объем микропор адсорбента?

Уравнение Дубинина-Радушкевича:

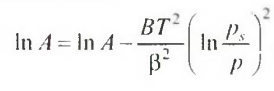, где , 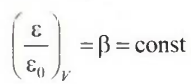коэффициент аффинности, р — равновесное давление паров над поверхностью адсорбента, ps — давление насыщенных паров над чистым жидким адсорбатом, A – величина адсорбции

Оно может быть использовано для определения объема микропор в адсорбенте. С этой целью экспериментальную изотерму адсорбции А = fiAp) строят в координатах уравнения

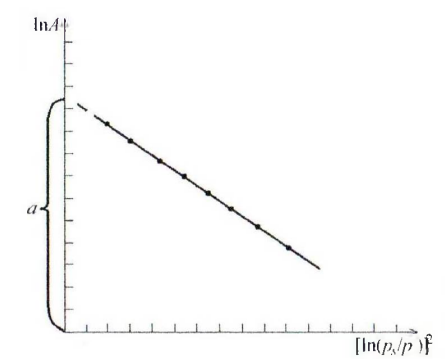
Как описать график:

ось y – lnA, ось x – (ln(ps/p))^2. Сверху оси y начинаем вести убывающую прямую Прямая доходит до оси y пунктиром, оси x не касается Расстояние от точки 0,0 то точки пересечения пунктира прямой с осью отмечаем буквой a Из сопоставления уравнения и риc. следует, что а = lnA0, a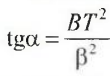 . Эти данные позволяют рассчитать по уравнению (Vm молярныйобъем жидкого адсорбата) суммарный объем микропор (максимальный адсорбционный объем) в единице массы или единице объема адсорбента:

номер 2

2. Напишите уравнение Стокса для скорости седиментации в гравитационном поле. Каковы условия применимости этого уравнения?

Седиментационный анализ в гравитационном поле применяется в основном для систем с довольно крупными частицами, таких как суспензии и эмульсии. Скорость осаждения для частиц сферической формы, выразив их объем V через радиус и учитывая, что в соответствии с законом Стокса коэффициент трения имеем:

V — объем частицы; g - ускорение свободного падения; р и ро - плотность частицы и дисперсионной среды соответственно. Полученное уравнение широко используется для определения размеров частиц по скорости их седиментации. Условия его применимости:

1. На практике частицы, как правило, имеют неправильную форму, и их коэффициент трения отличается от коэффициента трения сферических частиц (он больше) ). При равной массе частица неправильной формы будет оседать медленнее, чем сферическая частица. Следовательно, при использовании уравнения для определения радиусов реальных частиц, расчет дает радиус сферической частицы, которая оседает с той же скоростью, что и несферическая. Этот радиус называют радиусом эквивалентной сферы

2. С ростом размеров частицы оседание с постоянной скоростью сменяется ускоренным режимом оседания и переходом в турбулентный режим обтекания частицы сплошной средой. В этих условиях закон Стокса не соблюдается и уравнение не может быть использовано Верхний предел применимости закона Стокса по величине радиуса частицы можно определить для каждой конкретной системы из совместного решения уравнения 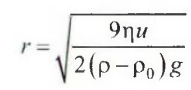и выражения для критерия Рейнольдса: отклонения от закона Стокса начинаются примерно при Re > 2

3. нижняя граница применимости закона Стокса определяется таким размером частиц, при котором они начинают участвовать в броуновском движении (несколько десятых долей микрометра)

4. В законе Стокса фигурирует вязкость дисперсионной среды, которая и определяет силу трения при прочих равных параметрах. При внутреннем трении закон Стокса соблюдается, при внешнем – нет

5. При малом размере частиц результаты измерения скорости седиментации могут быть искажены за счет наличия у частиц развитых поверхностных слоев, возникающих из-за наличия ДЭС и сильной гидратации.

номер 3

3. Рассчитайте ζ-потенциал частиц бентонитовой глины по следующим данным: при электрофорезе частицы глины перемещаются за 15 минут на 6 мм к аноду, Напряжение, приложенное к электродам, равно 100В, расстояние между электродами 30 см. Диэлектрическая проницаемость воды составляет 78,2, вязкость воды примите равной 0,89 мПа*с.

номер 4

4. Среднеквадратичное значение проекции смещения частиц гидрозоля

металлического серебра в воде за 2 секунды составляет 9 мкм. Рассчитайте радиус частиц, если вязкость среды равна 0,8 мПа*с при температуре 30°С.