Вариант 6 (их три, спроси какой)
номер
1
1. Каким образом можно сформировать на поверхности частиц CaF2, находящихся в водном растворе положительный а также отрицательные электрический заряд?
Для формирования заряда необходимо добавить сильный электролит:
Добавим Ca(NO3)2 и поверхность зарядится положительно из-за избытка катионов Ca
{[CaF2]n*mCa^(2+)*2(m-x)NO3^(-)}*2xNO3^(-)
где n - число молекул в кристалле (агрегате); m - число потенциалопределяющих ионов; (m — х) — число противоионов в слое Гельмгольца; х - число ионов в диффузном слое
Добавляем KF и поверхность зарядится отрицательно из-за избытка анионов F^(-) {[CaF2]n*mF^(-)*(m-x)K(+)}*xK(+)
номер 2
2. Как связана скорость схождения частицы в гравитационном поле с дисперсностью? Приведите уравнение.
Седиментационный анализ в гравитационном поле применяется в основном для систем с довольно крупными частицами, таких как суспензии и эмульсии. Скорость осаждения для частиц сферической формы, выразив их объем V через радиус и учитывая, что в соответствии с законом Стокса коэффициент трения имеем:
V — объем частицы; g - ускорение свободного падения; р и ро - плотность частицы и дисперсионной среды соответственно. Дисперсность - признак объекта коллоидной химии и одновременно параметр, характеризующий степень раздробленности дисперсной фазы, определяемый как величина, обратная определяющему (минимальному) размеру элемента дисперсной фазы. D=1/d (d – диаметр частицы), d=2r тогда r=1/(2D), следовательно:
номер 3
3. Определите общий объем микропор в одном килограмме канальной сажи на основе данных об адсорбции паров бензола (пользуясь уравнением Дубинина - Радушкевича). Плотность бензола 0,88 г/см3, t=25C
Как объяснить график:
Ось x это (ln(ps/p))^2, ось y это ось lnA
Должна получиться убывающая кривая По оси x взять шаг 0,2=1 полная клетка, по оси y взять шаг 0,1=1 полная клетка Нужно провести что-то вроде линии тренда по полученным точка и продолжить пунктиром линию до пересечения с осью lnA Полученное значение и будет значением для дальнейших расчетов (в данном случае lnA0=0,73)
номер 4
4. Во сколько раз изменится толщина диффузной части ДЭС частицы дисперсной фазы при 293К в водном растворе, содержащим 6*10^(-3) моль/л NaCl, если к 1 л этого раствора добавить 0,02 г Ba(No3)2 (M=261,3). Добавляемый электролит можно рассматривать как индифферентный.
Вариант 7 (их четыре, спроси какой)
номер 1
1. Приведите вид характеристической кривой адсорбции и укажите ее особенности. Что такое коэффициент аффинности характеристических кривых?
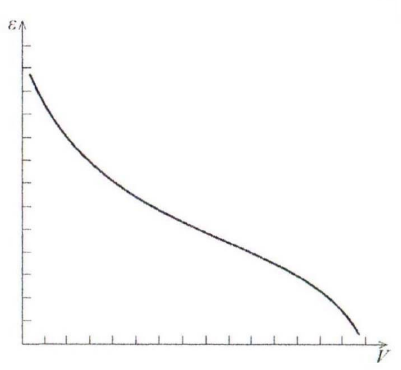
Как описать график:
ось y – E круглая, ось x – V. Сверху оси y начинаем вести убывающую кривую, которая формирует небольшую вогнутость, а затем начинает формировать небольшую выпуклость и почти доходит до оси x
характеристическая кривая обладает температурной инвариантностью, так как дисперсионные силы нс зависят от температуры:
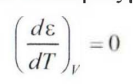
Температурная инвариантность означает, что точки с изотерм адсорбции, измеренных при разных температурах, попадают на одну и ту же характеристическую кривую. Это открывает возможность расчета изотермы адсорбции для любой желаемой температуре, если она известна хотя бы при одной.
Характеристические кривые, измеренные для разных адсорбатов и одного и того же микропористого адсорбента, обладают свойством аффинности. Это означает, что отношение значения адсорбционного потенциала ε для данного адсорбата к адсорбционному потенциалу другого адсорбата ε0, принятому за стандарт, является величиной постоянной при любом одинаковом значении адсорбционного объема:
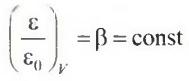
Параметр β называют коэффициентом аффинности.
Знание коэффициента аффинности для исследуемого адсорбата позволяет рассчитать его изотерму адсорбции.
Для
этого, зная характеристическую кривую
для стандарта
,
сначала рассчитывают характеристическую
кривую для данного адсорбата ε = f(V),
используя уравнение для коэффициента
аффинности. Затем по уравнениям
и
рассчитывают
значения А и р, получая тем самым изотерму
адсорбции
номер 2
2. Какие факторы влияют на ζ-потенциал? Каким образом можно уменьшить или увеличить ζ-потенциал в дисперсных системах?
Потенциал ζ (дзета), соответствующий плоскости скольжения и являющийся частью потенциала диффузного слоя, называется электрокинетическим или дзета-потенциалом.
Используя уравнение Гуи - Чепмена (где х - расстояние от начала диффузной части ДЭС, к - величина, обратная толщине диффузного слоя k=1/λ) при х = I, можно записать:
Из уравнения следует, что за толщину диффузного слоя (или диффузной части ДЭС) принимается такое расстояние λ = 1/к , на котором потенциал (φδ) уменьшается в число раз, равное основанию натуральных логарифмов е. В соответствии с теорией Гуи - Чепмена толщина диффузного слоя рассчитывается по следующему соотношению:
Как видно из уравнения, на толщину диффузного слоя влияют такие параметры дисперсной системы, как температура, диэлектрическая проницаемость среды(ε), ионная сила(I), они же будут влиять и на величину дзета-потенциала. При этом введение электролитов в дисперсионную среду играет особую роль, поскольку за счет таких добавок можно не только изменить толщину диффузного слоя и величину электрокинетического потенциала, но и изменить знак дзета-потенциала
Дзета потенциал имеет тот же знак, что и потенциалопределяющие ионы
С ростом ε и Т и уменьшением I λ растет следовательно растет и дзета-потенциал и наоборот
номер 3
3. Рассчитайте по уравнению Ленгмюра адсорбцию пропионовой кислоты из раствора с концентрацией 0,5 моль/л на поверхности раздела водный раствор - воздух при 295К, если известно поверхностное натяжение воды σ0 = 72,24 мДж/м2, поверхностное натяжение этого раствора σ = 55,6 мДж/м2 и константа уравнения Ленгмюра К = 7,73 л/моль.
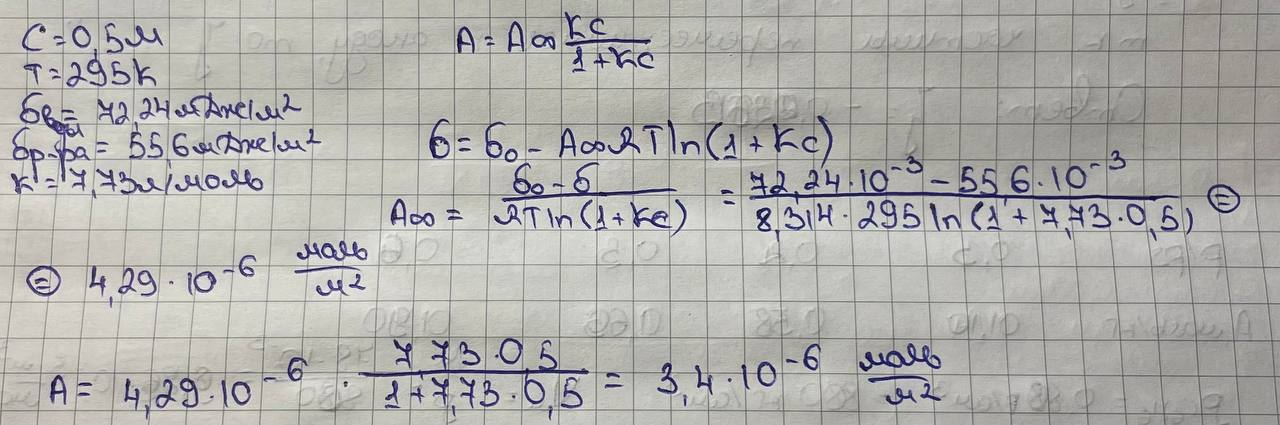
номер 4
4. Рассчитайте средний сдвиг сферических частиц оксида алюминия t = 20°с. за 1 с и скорость их седиментации при следующих условиях: вязкость среды 1 мПа*с, плотность среды 1 г/см3, плотность дисперсной фазы 3,9 г/см3, удельная поверхность частиц 5*10^6 м(-1).
