Вариант 6 (их три, спроси какой)
номер 1
1. Каким образом можно сформировать на поверхности частиц ВаЅO4, находящихся в водном растворе, положительный или отрицательный электрический заряд?
Для формирования заряда необходимо добавить сильный электролит:
Добавим Ba(NO3)2 и поверхность зарядится положительно из-за избытка катионов Ba
{[BaSO4]n*mBa^(2+)*2(m-x)NO3^(-)}*2xNO3^(-)
где n - число молекул в кристалле (агрегате); m - число потенциалопределяющих ионов; (m — х) — число противоионов в слое Гельмгольца; х - число ионов в диффузном слое
Добавляем K2SO4 и поверхность зарядится отрицательно из-за избытка анионов SO4^(2-) {[BaSO4]n*mSO4^(2-)*2(m-x)K^(+)}*2xK^(+)
номер 2
2. Во сколько раз изменится скорость осаждения частиц дисперсной фазы, если дисперсность уменьшится в три раза? Какие ограничения по применению уравнения Стокса для седиментации в гравитационном поле существуют со стороны дисперсности и почему?
Седиментационный анализ в гравитационном поле применяется в основном для систем с довольно крупными частицами, таких как суспензии и эмульсии. Скорость осаждения для частиц сферической формы, выразив их объем V через радиус и учитывая, что в соответствии с законом Стокса коэффициент трения имеем:
V — объем частицы; g - ускорение свободного падения; р и ро - плотность частицы и дисперсионной среды соответственно. Дисперсность - признак объекта коллоидной химии и одновременно параметр, характеризующий степень раздробленности дисперсной фазы, определяемый как величина, обратная определяющему (минимальному) размеру элемента дисперсной фазы. D=1/d (d – диаметр частицы), d=2r тогда r=1/(2D), следовательно:
Скорость
осаждения увеличится в 9 раз
Верхний
предел применимости
закона Стокса по величине радиуса
частицы можно определить для каждой
конкретной системы из совместного
решения уравнения
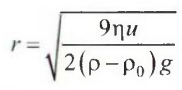и выражения для критерия Рейнольдса:
отклонения от закона Стокса начинаются примерно при Re > 2
задаться плотностью частиц 2,2 г/см3 (кварц), а в качестве дисперсионной среды использовать воду при комнатной температуре, то решение вышеуказанных уравнений для этих условий даст предельный радиус частиц —70 мкм
(с ростом размера частиц оседание сменяется ускоренным режимом оседания и переходом в турбулентный режим)
нижняя граница применимости закона Стокса определяется таким размером частиц, при котором они начинают участвовать в броуновском движении (несколько десятых долей микрометра), но уже при размере частиц порядка одного микрометра их скорость седиментации становится настолько малой, что сс точное измерение становится затруднительным с экспериментальной точки зрения.
номер 3
3. Определите общий объем микропор (м3/кг) сажи (по уравнению Дубинина-Радушкевича), используя данные об адсорбции бензола на саже. Плотность бензола 0,8 г/см3.
(таблица)
Как объяснить график:
Ось x это (ln(ps/p))^2, ось y это ось lnA
Должна получиться убывающая кривая По оси x взять шаг 1=2 полных клетки, по оси y взять шаг -0,2=1 полная клетка Нужно провести что-то вроде линии тренда по полученным точкам и продолжить пунктиром линию до пересечения с осью lnA Полученное значение и будет значением для дальнейших расчетов (в данном случае lnA0=-0,22)
номер 4
4. Рассчитайте электрокинетический потенциал частиц корунда в водном растворе электролита по следующим данным: скорость электроосмоса через корундовую мембрану 1,8 мл/мин, удельная электропроводность раствора 1,1·10^(-2) См·м(-1), поверхностная проводимость 1,9·10^(-2) См*м(-1), вязкость раствора 1 мПа·с, сила тока 9·10^(-3) А, диэлектрическая проницаемость раствора 80,1.
