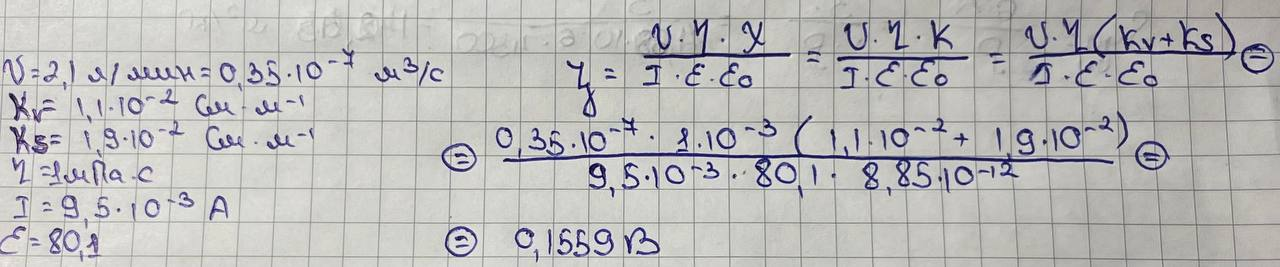Вариант 5 (их три, спроси какой)
номер
1
1. Каковы особенности адсорбции на микропористых адсорбентах? Какая теория (приведите уравнение) используется в этом случае?
микропористые:
rпор 0,5-1,5 нм Sуд 500÷1000 м2/г
основной особенностью адсорбции в микропорах является близость размеров пор и размеров молекул адсорбата. Из-за этого при адсорбции наблюдается ситовой эффект, то есть адсорбат, молекулы которого способны проникать в микропоры, адсорбируется значительно лучше, чем адсорбат с более крупными молекулами. В силу малого размера микропор, поля молекулярных сил противоположных стенок пор перекрываются, вследствие чего энергия взаимодействия молекулы адсорбата с окружающими ее стенками поры оказывается повышенной (как и теплота адсорбции). Все это способствует повышенной адсорбционной способности и селективности адсорбции.
Какими теориями описать адсорбцию:
Поляни
, где
Как описать график:
ось y – E круглая, ось x – V. Сверху оси y начинаем вести убывающую кривую, которая формирует небольшую вогнутость, а затем начинает формировать небольшую выпуклость и почти доходит до оси x
Объемного заполнения микропор
обобщенное уравнение изотермы адсорбции теории объемного заполнения микропор
Для многих микропористых активных углей n = 2. С учетом этого, уравнение принимает вид:
уравнение Дубинина-Радушкевича
Как описать график:
ось y – lnA, ось x – (ln(ps/p))^2. Сверху оси y начинаем вести убывающую прямую Прямая доходит до оси y пунктиром, оси x не касается Расстояние от точки 0,0 то точки пересечния пунктира прямой с осью отмечаем буквой a
номер 2
2. Приведите количественную зависимость среднего квадратичного сдвига
при броуновском движении от дисперсности.
Среднеквадратичный сдвиг зависит от T системы, вязкости дисперсионной среды и размера частиц, пропорционален квадратному корню из времени Броуновское движение должно быть тем интенсивнее, чем выше температура и чем меньше размер частиц
номер 3
3. Рассчитайте по уравнению Ленгмюра адсорбцию пропионовой кислоты из раствора с концентрацией 0,6 моль/л на поверхности раздела раствор-воздух при 25С, если известно поверхностное натяжение воды 72,24 мДж/м2, поверхностные натяжение этого раствора 55,6 мДж/м2 и константы уравнения Ленгмюра К=6,6 л/моль.
номер 4
4. Рассчитать электрофоретическую подвижность (м2/В*с) частицы корунда в водном растворе, если известно, что объемная скорость электроосмоса через корундовую диаграмму в том же растворе составляет 2*10^(-8) м3/с, удельная электропроводность раствора 1,2*10^(-2) Ом(-1)*м(-1), поверхностная проводимость 2*10^(-2) Ом(-1)*м(-1), сила тока при электроосмосе 4,5*10^(-2) А.
Вариант 6 (их три, спроси какой)
номер 1
1. Напишите уравнения состояния газообразных адсорбционных пленок. Как в них учитываются собственные размеры молекул ПАВ и их когезионное взаимодействие?
область низких концентраций
При низких концентрациях ПАВ в водном растворе изотерма поверхностного натяжения имеет линейный вид и описывается следующим уравнением:
где σ и σ0 – поверхностные натяжения раствора и растворителя, соответственно, R – универсальная газовая постоянная, Т – температура, Kг – константа Генри, С – концентрация раствора
, где поверхностное давление адсорбционной пленки (давление двухмерного газа)
Так как величина адсорбции А имеет размерность моль/м^2 , то величина обратная 1/А будет иметь размерность м^2/моль, то есть это площадь, занимаемая одним молем молекул в адсорбционном слое. Обозначим 1/А = Sм и с учетом этого перепишем уравнение
соотношение является аналогом уравнения Клапейрона-Менделеева для идеального газа pV= RT (для одного моля молекул):
область высоких концентраций
изотерма поверхностного натяжения описывается уравнением Шишковского:
Далее будем рассматривать такую область концентраций, в которой , тогда:
Воспользуемся уравнением Ленгмюра в линейной форме
из которого выразим и подставим в уравнение:
, введем обозначения 1/А = Sм и и получим:
Уравнение представляет собой уравнение состояния двухмерного газа, в котором учтены собственные размеры молекул, так как величина , а емкость монослоя Абеск определяется собственными размерами молекул адсорбата
Для описания свойств адсорбционной пленки при еще более высоких концентрациях ПАВ (более высокой величине адсорбции) может быть использовано уравнение состояния с двумя константами (А.Н. Фрумкин):
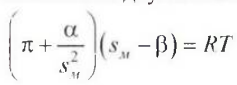здесь
в уравнении альфа
которое является аналогом уравнения Ван-дер-Ваальса с двумя константами:
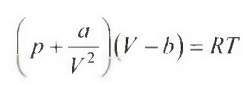здесь
в уравнении а
Константы альфа и а в этих уравнениях введены для учета межмолекулярных взаимодействий, которые начинают проявлять себя в области более высоких давлений, то есть когда число молекул на единице поверхности (или в единице объема) становится достаточно большим
Поведение молекул в адсорбционной пленке подобно поведению молекул в трехмерном пространстве. Чем выше их число на единице поверхности, то есть чем выше величина адсорбции, тем сильнее отличается их поведение от поведения молекул идеального газа, молекулы которого не имеют собственных размеров и не взаимодействуют друг с другом. Проводя эту аналогию дальше, можно предполагать, что у адсорбционных пленок должны наблюдаться те же агрегатные состояния, что и у обычных веществ
номер 2
2. Во сколько раз изменится скорость осаждения частиц дисперсной фазы, если дисперсность уменьшится в три раза? Какие ограничения по применению уравнения Стокса для седиментации в гравитационном поле существуют со стороны дисперсности и почему?
Седиментационный анализ в гравитационном поле применяется в основном для систем с довольно крупными частицами, таких как суспензии и эмульсии. Скорость осаждения для частиц сферической формы, выразив их объем V через радиус и учитывая, что в соответствии с законом Стокса коэффициент трения имеем:
V — объем частицы; g - ускорение свободного падения; р и ро - плотность частицы и дисперсионной среды соответственно. Дисперсность - признак объекта коллоидной химии и одновременно параметр, характеризующий степень раздробленности дисперсной фазы, определяемый как величина, обратная определяющему (минимальному) размеру элемента дисперсной фазы. D=1/d (d – диаметр частицы), d=2r тогда r=1/(2D), следовательно:
Скорость
осаждения увеличится в 9 раз
Верхний
предел применимости
закона Стокса по величине радиуса
частицы можно определить для каждой
конкретной системы из совместного
решения уравнения
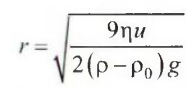и
выражения для критерия Рейнольдса:
отклонения
от закона Стокса начинаются примерно
при Re > 2
задаться плотностью частиц 2,2 г/см3 (кварц), а в качестве дисперсионной среды использовать воду при комнатной температуре, то решение вышеуказанных уравнений для этих условий даст предельный радиус частиц —70 мкм
(с ростом размера частиц оседание сменяется ускоренным режимом оседания и переходом в турбулентный режим)
нижняя граница применимости закона Стокса определяется таким размером частиц, при котором они начинают участвовать в броуновском движении (несколько десятых долей микрометра), но уже при размере частиц порядка одного микрометра их скорость седиментации становится настолько малой, что сс точное измерение становится затруднительным с экспериментальной точки зрения.
номер 3
3. Ниже приведены изотермы адсорбции и десорбции паров воды в порах активного угля при 298К:
(таблица) Рассчитайте и постройте интегральную кривую распределения объема пор по размерам. Плотность воды 1,0 г/см3, Ps = 2338 Па, σ = 71,96 мДж/м2.
Как объяснить график:
Ось x это r, нм, ось y это ось Vп/Vп,max,%
Должна получиться возрастающая кривая, создающая выпуклость
По оси x взять шаг 1=1 полная клетка, по оси y взять шаг 10=половина полной клетки
Знак вопроса у значения радиуса 2, посчитано все верно, но выпадает, возможно стоит уточнить у препода все ли ок в условии
номер 4
4. Рассчитайте электрокинетический потенциал частиц корунда в водном растворе электролита по следующим данным: скорость электроосмоса через корундовую мембрану 2,1 мл/мин, удельная электропроводность раствора K, = 1,1*10^(-2) См*м(-1), поверхностная проводимость K = 1,9*10^(-2) См*м3, вязкость раствора 1 мПа*с, сила тока 9,5*10^(-3) А, диэлектрическая проницаемость раствора 80,1.
В
дано скорость в мл/мин (я не дописала на
фотке)
