
решение идз 4 из пособия вариант 7
.docx-

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Институт (факультет)
Компьютерных наук
Кафедра
Прикладной математики
Индивидуальное домашнее заданий №4
По дисциплине: «Дискретная математика».
На тему: «Полнота систем булевых функций.»
-
Студент
АС-23-2
Корниенко А.С.
группа
подпись, дата
фамилия, инициалы
Руководитель
Жихорева С.В.
ученая степень, ученое звание
подпись, дата
фамилия, инициалы
Липецк 2024
Вариант 7.
№1 Систему из 3-х булевых функций исследовать на полноту с помощью теоремы Поста.
1. Система булевых функций от 2-х переменных f1(x,y) = x ∧ y ↑ x f2(x,y) = x ∨ y ∧ ¬x ↑ y f3(x,y) = ¬x ~ y ⊕ ¬y ↓ x ∧ y
Рассмотрим функцию f1(x,y)
= x ∧
y | x = ¬((x
∧ y)
∧ x)
а)
f1(x,y)
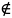 T0, т.к. f1(0,0)
= 1
б) f1(x,y)
T1, т.к. f1(1,1)
= 0
T0, т.к. f1(0,0)
= 1
б) f1(x,y)
T1, т.к. f1(1,1)
= 0
в) найдем двойственную функцию к данной f∗1(x,y) = x ∨ y ↑ x
x |
y |
f1(x,y) |
f∗1(x,y) |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
Функция не самодвойственна. f1(x,y) S, т.к. f∗1(x,y) ≠ f1(x,y);
г) f1(x,y) M, т.к. для векторов, находящихся в отношении предшество-
вания , не выполняется неравенство (0,0)⪯(0,1),(0,0)⪯(1,0),(0,1)⪯(1,1),(1,0)⪯(1,1).
д)
f1(x,y)
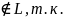 содержит
нелинейный элемент x∧y.
содержит
нелинейный элемент x∧y.
Рассмотрим функцию f2(x,y) = x ∨ y ∧ ¬x ↑ y
а) f2(x,y) T0, т.к. f1(0,0) = 1 б) f2(x,y) T1, т.к. f1(1,1) = 0
в) найдем двойственную функцию к данной
f∗2(x,y) = x ∧ y ∨ ¬x ↑ y
x |
y |
f2(x,y) |
f∗2(x,y) |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
f2(x,y)
 S.
S.
г) f2(x,y) M.
д) f2(x,y)
 .
.
Рассмотрим функцию f3(x,y) = ¬x ~ y ⊕ ¬y ↓ x ∧ y
а) f3(x,y) T0, т.к. f1(0,0) = 0 б) f3(x,y) T1, т.к. f1(1,1) = 1
в) найдем двойственную функцию к данной
f∗3(x,y) = ¬x ~ y ⊕ ¬y ↓ x ∨ y
x |
y |
f3(x,y) |
f∗3(x,y) |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
f3(x,y) S.
г) f3(x,y) M.
д) f3(x,y) .
Составим таблицу
Класс Функция |
T0 |
T1 |
S |
M |
L |
f1(x,y) |
- |
- |
- |
- |
- |
f2(x,y) |
- |
- |
|
- |
- |
f3(x,y) |
+ |
+ |
+ |
+ |
- |
В каждом столбце таблицы есть хотя бы один «–», следовательно, по тео-
реме Поста, данная система булевых функций является полной.
2. Система булевых функций от 3-х переменных f1(x,y,z) = x∧z∨y f2(x,y,z) = ¬x ↓ y ⊕ ¬z ↑ y
f3(x,y,z) = z⊕¬y∧x→x∨¬z
Рассмотрим функцию f1(x,y,z) = x∧z∨y а) f1(x,y,z) T0, т.к. f1(0,0,0) = 0 б) f1(x,y,z) T1, т.к. f1(1,1,1) = 1
в) найдем двойственную функцию к данной f∗1(x,y,z) = x∨z∧y
x |
y |
z |
f1(x,y,z) |
f∗1(x,y,z) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Функция не самодвойственна. f1(x,y,z) S, т.к. f∗1(x,y,z) ≠ f1(x,y,z).
г) f1(x,y,z) M.
д) f1(x,y,z) .
Рассмотрим функцию f2(x,y,z) = ¬x ↓ y ⊕ ¬z ↑ y
а) f2(x,y,z) T0, т.к. f1(0,0,0) = 1 б) f2(x,y,z) T1, т.к. f1(1,1,1) = 0
в) найдем двойственную функцию к данной
f∗2(x,y,z) = ¬x ↓ y ⊕ ¬z ↑ y
x |
y |
z |
f2(x,y,z) |
f∗2(x,y,z) |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
f2(x,y,z) S.
г) f2(x,y,z) M.
д) f2(x,y,z) .
Рассмотрим функцию f3(x,y,z) = z⊕¬y∧x→x∨¬z
а) f3(x,y,z) T0, т.к. f1(0,0,0) = 1 б) f3(x,y,z) T1, т.к. f1(1,1,1) = 1
в) найдем двойственную функцию к данной
f∗3(x,y,z) = z⊕¬y∨x→x∧¬z
x |
y |
z |
f3(x,y,z) |
f∗3(x,y,z) |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
f3(x,y,z) S.
г) f3(x,y,z) M.
д) f3(x,y,z) .
Составим таблицу
Функция Класс |
T0 |
T1 |
S |
M |
L |
f1(x,y,z) |
+ |
+ |
- |
+ |
- |
f2(x,y,z) |
- |
- |
+ |
- |
- |
f3(x,y,z) |
- |
+ |
- |
- |
- |
В каждом столбце таблицы есть хотя бы один «–», следовательно, по тео-
реме Поста, данная система булевых функций является полной.
3. Система булевых функций от 4-х переменных f1(x,y,z,t) = y∨t≡x↓z f2(x,y,z,t) = y∧x⊕z≡t→x
f3(x,y,z,t) = y→ x∨t⊕z∧y≡x
Рассмотрим функцию f1(x,y,z,t) = y∨t≡x↓z а) f1(x,y,z,t) T0, т.к. f1(0,0,0,0) = 0 б) f1(x,y,z,t) T1, т.к. f1(1,1,1,1) = 0
в) найдем двойственную функцию к данной
f∗1(x,y,z,t) = y∧t≡x↓z
t |
x |
y |
z |
f1(x,y,z,t) |
f∗1(x,y,z,t) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
Функция не самодвойственна. f1(x,y,z,t) S, т.к. f∗1(x,y,z,t) ≠ f1(x,y,z,t).
г) f1(x,y,z,t) M.
д) f1(x,y,z,t) .
Рассмотрим функцию f2(x,y,z,t) = y∧x⊕z≡t→x
а) f2(x,y,z,t) T0, т.к. f1(0,0,0,0) = 1 б) f2(x,y,z,t) T1, т.к. f1(1,1,1,1) = 0
в) найдем двойственную функцию к данной
f∗2(x,y,z,t) = y∨x⊕z≡t→x
t |
x |
y |
z |
f2(x,y,z,t) |
f∗2(x,y,z,t) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
f2(x,y,z,t) S.
г) f2(x,y,z,t) M.
д) f2(x,y,z,t) .
Рассмотрим функцию f3(x,y,z,t) = y→ x∨t⊕z∧y≡x
а) f3(x,y,z,t) T0, т.к. f1(0,0,0,0) = 0 б) f3(x,y,z,t) T1, т.к. f1(1,1,1,1) = 0
в) найдем двойственную функцию к данной
f∗3(x,y,z,t) = y→ x∧t⊕z∨y≡x
t |
x |
y |
z |
f3(x,y,z,t) |
f∗3(x,y,z,t) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
