Деонтическая модальность суждений, её значение для построения нормативных суждений

Деонтическая модальность – это выраженная в суждении просьба, совет, приказ или предписание, побуждающее кого-либо к конкретным действиям.

Среди предписаний стоит выделить нормативные предписания и нормы права (правообязывающие, правозапрещающие, правопредставляющие).

В правоотношении праву всегда соответствует обязанность, и наоборот, и выражаются как О-обязывающие, F-запрещение, Р – разрешение, символом d- регулируемое действие, символами x,y,z – субъекты правоотношений).

Рационально построенная нормативно-правовая система должна удовлетворять минимальные модальные деонтические требования: непротиворечивости, сбалансированности, полноты.

Понятие как форма мышления. Содержание и объём понятия. Закон обратного отношения между содержанием и объёмом понятия.

Понятие – это форма мышления, отражающая предметы в их существенных признаках. Признак предмета - то, в чем предметы сходны или чем они отличаются друг от друга.

Содержание понятия - мыслимая в понятии совокупность существенных признаков предмета.

Понятие как форма мышления отражает предметы в абстрактной, обобщенной форме на основании их существенных признаков.

Понятие – одна из основных форм научного познания. Формируя понятия, наука отображает в них изучаемые ею предметы, явления, процессы. Для образования понятия необходимо выделить существенные признаки предмета, применяя логические приемы: сравнение, анализ, синтез, абстрагирование, обобщение.

Содержание понятия – это совокупность признаков, на основе которых в нем обобщаются и выделяются предметы определенного класса. Основное содержание понятия составляет совокупность признаков, каждый из которых, взятый отдельно, необходим, а все вместе достаточны,чтобы с их помощью можно было отличить данный предмет от других.

Объем понятия – это множество объектов, выделяемых и обобщаемых в данном понятии.

Объем понятия может быть бесконечным, а может быть и пустым.

Об отдельном объекте, из числа тех, что образуют данное множество, этот объект входит в данное множество.

Между множествами может быть установлено отношение включения. Операции множества удобно изображать на кругах Эйлера.

Пересечением множеств А и Б называется множество тех элементов, которые одновременно входят в А и Б.

Объединением множеств А и Б называется множество элементов, которые входят в А или в Б.

Правило объема: каждый элемент объема понятия имеет все признаки, перечисленные в содержании понятия.

Связь объема и содержания понятия выражается в законе обратного отношения между ними.

Закон обратного отношения между объемом и содержанием понятия: увеличение содержания понятия ведет к образованию понятий с меньшим объемом, и наоборот. Таким образом содержание и объем понятия тесно связаны друг с другом.

Объем понятия - совокупность предметов, мыслимая в понятии.

Содержанием понятия - мыслимая в понятии совокупность существенных признаков предмета.

Объем понятия составляет логический класс (множество), который может включать в себя подкласс (подмножество). Пример: А-следователи, В – юристы.

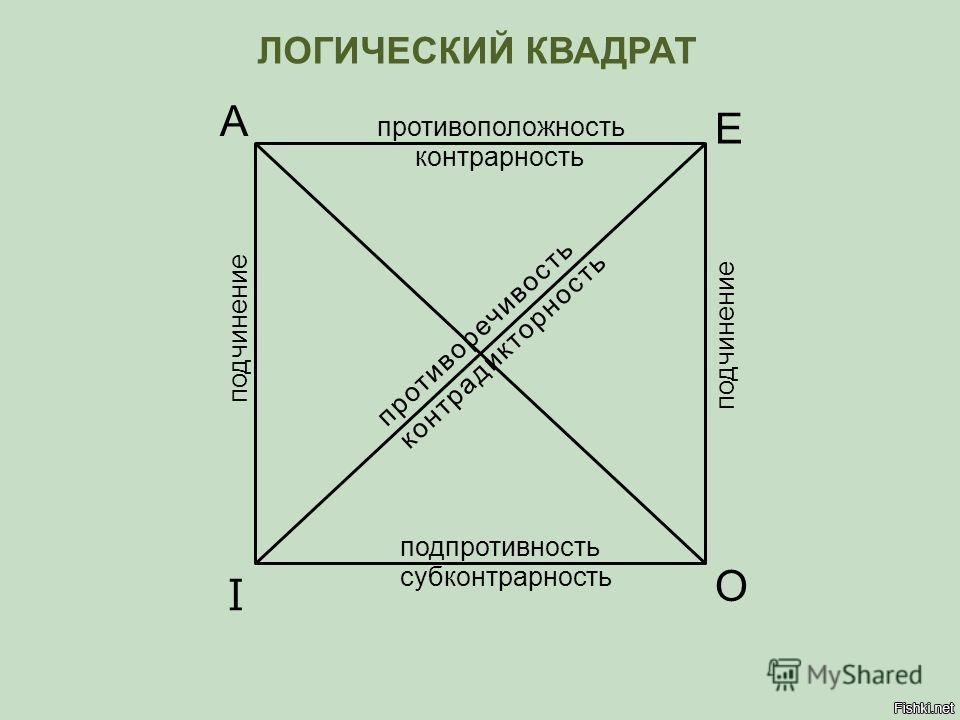
Отношения между простыми суждениями. Логический квадрат.

Суждения делятся на сравнимые и несравнимые.

Сравнимые - имеют одинаковый субъект и различающейся связкой или квантором (все студенты ходят в институт и все студенты не ходят в школу).

Несравнимые - имеют разные субъекты и предикаты (некоторые студенты первокурсники и некоторые студенты заочники).

Эти отношения обычно рассматриваются при помощи логического квадрата, его вершины символизируют простые категорические суждения - АЕIО, стороны диагонали — отношения между суждениями.

Среди сравнимых различают совместимые и несовместимые суждения.

Совместимые - суждения, которые одновременно могут быть истинными, бывают 3 вида совместимости:

- эквивалентность (суждения, имеющие одинаковый логические характеристики: одинаковые субъект и предикат, однотипную связку, количественную и качественную характеристику). С помощью логического квадрата данные отношения не регистрируются.

- частичная совместимость характерна для суждений I и O, которые могут быть одновременно истинными, но не могут быть одновременно ложными ( например при ложности суждения «некоторые злакт ядовиты», будет истинно суждение «некоторые злаки не являются ядовитыми», так же они могут быть одновременно истинными).

- подчинение имеет место между суждениями А и I, Е и О, где при истинности общего суждения частное всегда будет истинным, а при ложности частного - общее тоже ложно (все хищения совершаются по неосторожности и некоторые хищения совершаются по неосторожности).

Несовместимыми - суждения А и Е, А и О, Е и I, которые одновременно не могут быть истинными:

Противоположные - суждения А и Е, которые одновременно не могут быть истинными, но могут быть одновременно ложными. ( ни один судья не является юристом и все судьи юристы, одно истинно).

Противоречащие - суждения А и О, Е и I, которые одновременно не могут быть ни истинными ни ложными (если истинно что все принципиальные люди признают свои ошибки, то ложно что некоторые принципиальные люде не признают своих ошибок).