10. Моделирование гауссовского случайного вектора с заданными средним и корреляционной матрицей.

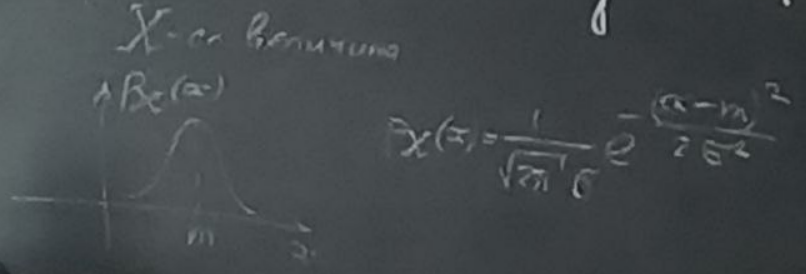
Задача решается в два этапа:

1. Формируется гауссовский случайный вектор

2. Формируем вектор с помощью линейного преобразования . 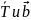– неизвестны. Нужно найти их.

Выполним операцию мат. ожидания над обеими матрицами. Получим:

Необходимо решить это квадратное матричное уравнение и найти 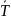. Из теории матриц известно разложение Холецкого. 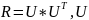– верхне-треугольная матрица

Для того чтобы существовало разложение Холецкого нужно, чтобы матрица была положительно-определённая.

Существует алгоритм вычисления разложения Холецкого, который реализован в Matlab’e:

T = chow(R)

Если функция выдаёт ошибку, значит разложение Холецкого вычислить невозможно. Задача формирования вектора тоже не имеет решения. Существуют критерии выяснения того, является ли матрица положительно-определённой. Самый известный – критерий Сильвестра.

Составим программу для решения задачи:

y = randn(n, 1);

T = Chow(R);

x = T * y + m;

В данном случае, мы снова воспользовались уже известным правилом: сначала формируем случайный вектор с простым распределением, а затем делаем его преобразование (в данном случае – линейное) и получаем нужный нам вектор со сложным законом распределения.

Для гауссовских случ. величин понятие независимости и некоррелированность одинаковы Формирование гауссовского случ. Вектора с корреляцией. Если случ. величина X увеличивается, то среднее X уменьшается, но не всегда.

Величину отношения между величинами определяет коэфф. корреляции (линейная вероят. зависимость). X = [x1, x2, x3] – вектор. Каждая величина обладает мат ожиданием. Из мат ожиданий можно составить вектор: M = [m1, m2, m3]. Обладают еще и дисперсия:

Коэффициент корреляции между случ. величинами Xi Xj [-1,1]

Rx = [rnn]

Корреляционная матрица R полностью характеризует все корреляционные взаимосвязи между компонентами случ. вектора X. Гауссовкский случ. вектор характеризуется: вектором мат ожидания и корреляционной матрицей. Задача: сформировать гауссовкский случ. вектор X с с мат ожиданием m и матрицей R.

Воспользуемся общим способом (1- формируем Гауссовский случ. вектор с некоррелированными компонентами, а потом преобразование в нужный вектор с коррелированными компонентами.)

Y – вектор, где my = 0, Ry = [1]

Линейное преобразование гауссовской случ. вектора приводит к гауссовскому случ. вектору. X = T * Y. Найти матрицу T. Rx = E{X * X^t} - ^t – транспонирование. Матрица T неизвестная, но не неслучайная.

Rx = E{X * X^t} –> T*E{Y * Y^t} T^t = T * T^t

Разложение Холецкого

X = T*Y + m*x

y = randn(n,1);

T = chol(Rx);

x = T*y + m;

Мы использовали известный подход: Вектор с простым распределением и потом сделать преобразование (у нас линейное) и получить нужный вектор.

Чтобы программа работала – матрица Rx должна быть положительно определенная. Существует возможность определить заранее, является ли матрица положительно определенная. Критерий Сильвестера.

Если матрица не является положительно определенной и функция chol дает ошибку, то исходная матрица не является исходной и задача не имеет решения.