Моделирование дискретных случайных величин.
При моделировании реальных объектов требуется учитывать влияние как внутренних, так и внешних случайных факторов.
Случайная величина – это числовая величина, которая может принимать случайное значение (заранее неизвестное). Пример: кол-во студентов, присутствующих на лекции.
Случайные величины: непрерывные и дискретные.
Случайная величина непрерывная, если она принимает непрерывное множество значений. Множество значений – континуум. (Примером непрерывной случайной величины является, например, дальность броска мяча.)
Дискретная случайная величина – случайная величина, множество значений которой счетно и можно пронумеровать (Пример: подбрасывание монеты, раздача колоды карт и т.д.)
Задача моделирования случайной величины состоит в создании алгоритма формировании (вычисления) значений случайных величин.
Нельзя предсказать значения случайных величин. Максимальном полном описании свойств случайных величин является ее функция распределения (или ее производная: плотность распределения).
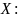
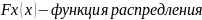
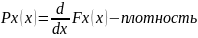
Алгоритм – последовательность операций. При моделировании необходимо получить значение, заданным функцией распределения. Для этого используются датчики случайных чисел.
Разработка датчика-отключения – сложная проблема, которая по-разному решается с помощью различных математических пакетов.
Команда rand генерирует случайное число или последовательность случайных чисел от 0 до 1, в результате чего получается график, изображённый на рис.2.
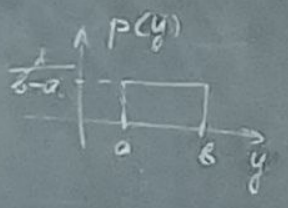
Рис.2 - График при работе команды rand
Но перед этим нужно произвести линейное преобразование по формуле Y = (b-a) * X + a. Данная формула пишется в программе MatLab в следующие две строки:
x=rand(i);
y=(b-a) *x + a;
Следует учесть, что случайная величина пишется с большой буквы, а её выборочная значение – с маленькой.
Формирование дискретной случайной величины с равновероятным распределением
При моделировании случайных величин формируется сначала случайная величина с простым законом распределения, а затем, на её основе, формируется желаемая для нас случайная величина (рис.3)
Рис.3 – Формулы моделирования случайных величин с равновероятным распределением
Сначала, формируем случайную величину, расположенную в интервале [0:1], установим порог = 0.5 и затем сравниваем выборочное значение x с порогом. В программе MatLab это будет выглядеть следующим образом:
% Генерация случайной величины в интервале [0, 1]
x = rand(1);
% Установка порога и формирование значения дискретной случайной величины
if x>= 0,5:
θ = 1 % Установка значения случайной величины, если x >= 0.5
else:
θ = 0 % Установка значения случайной величины, если x < 0.5
end;
При однократном запуске данного кода мы получаем одно значение величины θ – либо 0 либо 1.
Формирование дискретной случайной величины с не равновероятным распределением
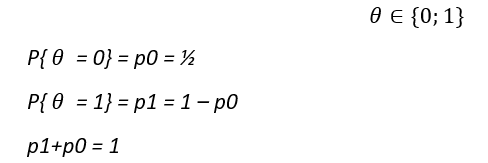
Рис.4 – Формулы моделирования случайных величин с не равновероятным распределением
При формировании кода программы в MatLab мы меняем порог, в результате чего код станет таким:
x = rand(1); % Генерируем случайное число в интервале [0, 1]
if x >= P0: % Проверяем, больше ли случайное число порога P0
θ = 1 % Если больше или равно P0, устанавливаем θ = 1
else:
θ = 0 % Если меньше P0, устанавливаем θ = 0
end;
При множественном запуске этой программы мы получаем последовательность двоичных случайных величин с заданной вероятностью появление 0.