3. Иерархия моделей. Адекватность и сложность модели. Иерархия моделей

Иерархия - совокупность некоторого количества моделей, возрастающих по сложности и по степени адекватности. В начале процесса моделирования составляется самая простая модель, затем она проверяется на сложность и степень адекватности – если достигнут желаемый уровень её адекватности либо предельный уровень её сложности, то процесс заканчивается, если нет – то добавляются другие элементы, которые учитывают дополнительные свойства объекта.

Адекватность модели

Адекватность модели понимают соответствие её свойств свойствам реального объекта. Адекватность модели зависит от решаемых задач: для одной задачи она может быть адекватна, для другой – нет.

Задача проверки адекватности модели возникает в течение всего процесса моделирования.

Недостатки модели:

1. Модель может содержать несущественные элементы

2. Модель может не содержать существенных элементов

3. Одна или больше существенных элементов могут быть представлены неточно.

Низшая ступени иерархии – самая простая модель – учитывает только основные свойства исследуемого объекта. Обычно неадекватна

Второй уровень иерархии - более сложная модель, с повышенной точностью

Если нас не устраивает точность модели, то надо учесть ещё больше свойств реального объекта и построить ещё более точную модель

Мы должны остановится либо, когда будет достигнута необходимая степень точности или адекватности модели, либо, когда модель станет недопустимо сложной.

4. Пример имитационной модели фильтра нижних частот.

Это базовая аналоговая схема, которая пропускает низкочастотные составляющие сигнала, а высокочастотные — подавляет.

Элементы цепи:

1. Входной сигнал (x(t)): Это входное напряжение (сигнал), которое подается на схему. Оно изменяется во времени.

2. Резистор (R): Элемент цепи, который оказывает сопротивление электрическому току. Он характеризуется сопротивлением, которое измеряется в Омах.

3. Конденсатор (C): Элемент, который накапливает электрический заряд. Его емкость измеряется в Фарадах.

4. Ток (i(t)): Это электрический ток, протекающий через резистор и заряжающий конденсатор. Он также изменяется во времени.

5. Напряжение на резисторе (Ur(t)): Это напряжение на резисторе.

6. Выходной сигнал (y(t) = Uc(t)): Это напряжение на конденсаторе, которое является выходным сигналом фильтра. Оно также изменяется во времени.

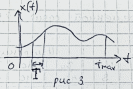
7. Рис. 2 – Графики входного воздействия (функция, существующая от 0 до t_max) и выходного сигнала (y(t))

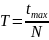
Как работает фильтр нижних частот (фнч): (не уверен)

1. Низкие частоты: Когда входной сигнал x(t) изменяется медленно (низкая частота), конденсатор успевает заряжаться и разряжаться почти мгновенно. В этом случае большая часть входного напряжения передается на выход, то есть на конденсатор, поэтому выходное напряжение y(t) примерно равно входному напряжению x(t).

2. Высокие частоты: Когда входной сигнал x(t) изменяется быстро (высокая частота), конденсатор не успевает полностью зарядиться и разрядиться, и большая часть входного напряжения падает на резисторе, в результате чего выходное напряжение y(t) значительно меньше входного x(t).

3. Пограничная частота: Существует определенная пограничная частота, называемая частотой среза, которая определяется значениями R и C. Она определяет границу между частотами, которые свободно проходят через фильтр, и частотами, которые существенно подавляются. Эта частота равна:

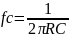
Для того, чтобы провести натурный эксперимент, нужно купить элементы (осциллограф – «О» и генератор сигнала «ГС») и составить схему. Но его проведение затруднительно в силу его высокой стоимости в основном за счёт стоимости генератора и осциллографа. Будем решать эту задачу методом математического моделирования.

На основе известных физических законов составим уравнение, описывающее моделируемую систему (электрическую цепь).

Для данной цепи работают следующие физические законы:

1. Второй закон Кирхгофа: x(t)=U_R(t)+y(t)

2. Закон Ома: U_R(t) = R * i(t)

3. Закон, связывающий ток через конденсатор и напряжение на конденсаторе:

Подставляем третью формулу во вторую, а затем получившуюся вторую в первую и получаем формулу:

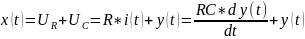
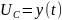
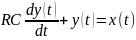– это уравнение (уравнение цепи) относится к классу линейных уравнений первого порядка, но с правой частью. Данное уравнение может быть решено аналитически, но его решение требует определённой математической квалификации. Поэтому применяем имитационного моделирования, чтобы не решать данное дифф. уравнение.

– последовательность отсчетов через равные промежутки времени. T – частота дискретизации.

Общее число отсчётов –

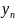– отсчёты выходного сигнала, которые требуется найти.

Производная.

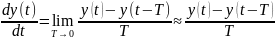
Заменяем производную разностным отношением, допуская при этом погрешность.

– берем при дискретизации

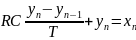
Мы получили разностное уравнение, относительно отсчётов, из дифференциального уравнения.

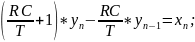
Для того, чтобы запустить этот вычислительный процесс требуется задать начальные условия

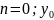– начальное условие (напряжение на конденсаторе)

Мы получили решение в виде рекуррентного выражения. Однако встаёт вопрос – как выбрать интервал дискретизации?

Составим программу:

% Расчет коэффициента 'a', который зависит от сопротивления R, емкости C и шага дискретизации T

a = 1 / (1 + ((R * C) / T));

% Расчет коэффициента 'b', который учитывает временные изменения, связанные с RC-схемой

b = ((R * C) / T) * a;

% Основной цикл расчета выхода y(n) для каждого дискретного шага времени

for n = 2:N

    % Вычисление текущего значения выхода y(n) на основе входного сигнала x(n) и предыдущего значения y(n-1)

    y(n) = a * x(n) + b * y(n - 1); 

end

plot(y); % Построение графика выходного сигнала y(n)

Чем ближе к нулю, тем точнее разностное отношение аппроксимирует (приближает) производную.

На практике, сначала берут произвольной величине, подсчитывают соответствующее ему число отсчётов и запускают программу.

Сначала берём , затем в 2 раза увеличиваем число отсчётов , получаем новый график, который не совпадает с исходным. Далее ещё раз увеличиваем число отсчётов 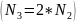и снова строим график. Продолжаем этот процесс до тех пор, пока график не перестанет изменяться.

Мы смогли получить ответ, не решая дифференциальное уравнение.

На практике значения элементов никогда не могут быть заданы точно.

- чем меньше погрешность изготовления, тем дороже.

Многократно запуская программу при различных можно выбрать элементы с допустимой погрешностью.

При эксплуатации нашего устройства в различных условиях значения элементов будут подвергаться случайным возмущениям (изменениям).

При более сложной схеме анализа с помощью программы недостаточно. Для этого потребуется учёт случайного характера значений элементов. При этом может понадобиться учёт зависимости значения элементов между собой. Возможна так же оптимизация параметров элементов по критерию минимума стоимости.