
- •Моделирование как метод исследования сложных систем связи и управления. Общие подходы.
- •Способы исследования реальных объектов:
- •Натурный эксперимент
- •Математическое моделирование
- •Имитационное моделирование
- •Классификация моделей
- •Этапы моделирования
- •Построение модели системы. Математическое моделирование. Имитационное моделирование.
- •Иерархия моделей. Адекватность и сложность модели. Иерархия моделей
- •Адекватность модели
- •Пример имитационной модели фильтра нижних частот.
- •Элементы цепи:
- •Как работает фильтр нижних частот (фнч): (не уверен)
- •Пример имитационной модели информационной системы.
- •Моделирование дискретных случайных величин.
- •Формирование дискретной случайной величины с равновероятным распределением
- •Формирование дискретной случайной величины с не равновероятным распределением
- •Формирование дискретной случайной величины с не равновероятным распределением и с числом значений больше 2
- •Моделирование непрерывных случайных величин с равномерным распределением.
- •Моделирование непрерывных случайных величин с гауссовским распределением.
- •Моделирование случайных векторов с независимыми компонентами
- •Моделирование гауссовского случайного вектора с заданными средним и корреляционной матрицей.
- •Модели каналов связи
- •Помехи в информационных системах.
- •Модели случайных процессов. Постоянный процесс. Винеровский процесс. Процессы авторегрессии различных порядков.
- •Идентификация модели авторегрессии на примере процесса авторегрессии 1-го порядка
- •Общая постановка задачи фильтрации в информационных системах. Нерекуррентная и рекуррентная фильтрация.
- •Фильтр Калмана и его свойства. Принцип предсказания и коррекции.
- •Вычислительная сложность алгоритма обработки сигналов в информационных системах. Функция сложности алгоритма.
- •Вычислительная сложность
- •Функция сложности алгоритма
- •Методы снижения сложности алгоритмов
- •Алгоритмы экспоненциальной и полиноминальной сложности. Порядок сложности алгоритмов.
- •Методы анализа сложности алгоритма. Непосредственный подсчет. Рекуррентная формула для асимптотической сложности. Оценка асимптотической сложности по рекуррентной формуле.
- •Анализ вычислительной сложности перемножения матриц и векторов
- •Методы снижения сложности алгоритмов.
- •Перемножение комплексных матриц и векторов
- •Перемножение двух комплексных матрицы
- •Метод Штрассена быстрого умножения матриц и его асимптотическая сложность.
- •Методы быстрого умножения комплексных чисел, векторов и матриц. Метод 3м.
Методы снижения сложности алгоритмов
Как правило, при решении задач моделирования оказывается, что выч. сложность алгоритма очень высока -> невозможно провести моделирование. Поэтому требуется решить задачу, упрощение (снижение сложности алгоритма, чтобы можно было в реальности провести моделирование).
Известно два подхода для снижения выч. сложности:
Результат работы алгоритма не изменяется
Вектор x -> Алгоритм-> вектор y
Вектор y = вектор F (вектор x)
Данный подход наиболее желателен, так как результат работы алгоритма тот же, а сложность меньше.
Применяется, когда подход первый невозможно применить или он себя исчерпал
Результат работы алгоритма изменяется (данные на выходе изменяются, но не очень существенно).
Вектор x -> Алгоритм-> вектор y с тильдой
Вектор y с тильдой = вектор Fс тильдой (вектор x)
Алгоритм изменяется, но не значительно изменяется. вектор y ~ y с тильдой.
Существенно можно снизить сложность, но будут потери. Рассматриваем ток первые подход. (сокращение сложности, без изменения результата)
Возможности снижения сложности без изменения выходных данных
Преобразования алгоритма с экспоненциальной сложность в полиноминальную. (На практике почти невозможно сделать): NP-> P
Снижение порядка сложности (Иногда возможно снизить): P: NK где K – порядок сложности
Снижение мультипликативной постоянной альфа в алгоритме с полиноминальной сложность. (Если есть алгоритм полиноминальный, у него есть коэффициент альфа на NK нет универсального способа уменьшения выч сложности алгоритма, но есть методы:
Метод «Разделяй и властвуй» - согласно этому методу, исходная сложная задача (большой размер входных данных) разбивается на нескольких простых задач. Каждая задача решается каким-либо методом. Затем решение подзадач комбинируется, а затем на их основе. Очень часто такой подход носит рекурсивный характер. (Пример: быстрое преобразование Фурье, алгоритм Штрассена для быстрого умножения матриц.)
Метод исключения повторяющихся операций. (выявить повторяющиеся операции и их исключить, самое трудное – найти повторяющиеся операции).
Задача перемножения двух комплексных чисел:
(a+jb)(c+jb) = (ac-bd)+j(bc+ad)
Одно комплексное число в компе – пара действительных чисел.
В данном случае результат – пара действительных чисел. 4 действительных умножения и 2 действительных сложения (действительные операции без j). Задача – сократить кол-во таких операций. Если для выполнение этих операций используется процессор без аппаратного умножения, то время операций умножения в разы больше, чем время операций сложения. Задача упрощение сводится к задаче сокращения кол-ва операций умножения

Рисунок 1 – Унгерн (Метод 3М)
Алгоритмы экспоненциальной и полиноминальной сложности. Порядок сложности алгоритмов.
Алгоритмы по скорости роста функции сложности делятся на классы:
Алгоритмы полиномиальной сложности

Алгоритмы экспоненциальной сложности
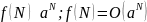
Обратимся
к алгоритмам полиномиальной сложности:
число
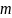 называется порядком сложности алгоритма.
называется порядком сложности алгоритма.
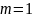 – алгоритм
с линейной сложностью (первого порядка)
– алгоритм
с линейной сложностью (первого порядка)

 – алгоритм
с квадратичной сложностью (второго
порядка)
– алгоритм
с квадратичной сложностью (второго
порядка) 
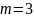 – алгоритм
с кубической сложностью (третьего
порядка)
– алгоритм
с кубической сложностью (третьего
порядка) 
При увеличении производительности вычислительного устройства в 1000 раз размер входных данных алгоритма 1-го порядка может быть увеличен тоже в 1000 раз. Для алгоритма 2-го порядка – только в 31 раз, а для алгоритма 3-го порядка только в 10 раз. Если требуется реализовывать полиномиальные алгоритмы высокого порядка или алгоритмы экспоненциальной сложности, то требования к производительности процессора катастрофически вырастают.



