17. Вычислительная сложность алгоритма обработки сигналов в информационных системах. Функция сложности алгоритма.

Алгоритм – последовательность операций/шагов/действий, которые нужно выполнить чтобы получить решение задачи.

Численные алгоритмы – последовательность аритмических операций, которые нужно выполнить для решения задач.

Желательные свойства алгоритмов:

1. Эффективность – выполнение алгоритма при любых допустимых исходных данных за заданное время;

2. Определённость - выполнение алгоритма при любых допустимых исходных данных за определённое время;

3. Конечность - выполнение алгоритма при любых допустимых исходных данных за конечное число шагов.

Для выбора наилучшего алгоритма, нужно посмотреть на количественные характеристики, которые позволяли бы сравнивать значения.

Вычислительная сложность

Время выполнение алгоритма зависит от числа арифметических операций, а также от производительности выч. устройств. размер памяти. Временная сложность алгоритма- число арифметических операций, которые требуется выполнить для реализации алгоритма.

Емкостная сложность – размер памяти, кот. требуется для реализации алгоритма.

Временная сложность – критичная для реализации алгоритма моделирования.

Алгоритм обрабатывает вектор входных данных (вектор x) и на выходе алгоритм вектор выходных данных (вектор y).

Вычислительная сложность зависит от самих входных данных и от размера входных данных.

Функция сложности алгоритма F (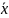 , n) – число операций, как функция от объёма входных данных n и от самих входных данных, вектор x.

Сложность алгоритма зависит от входных данных- это есть случ. функция.

Функция сложности алгоритма

При моделировании используются алгоритмы, сложность которых не зависит от самих входных данных. Функция всегда возрастающая. Для практической реализации алгоритмов, возникающих при моделировании, необходимо знать с какой скоростью растёт функция сложности. Введём понятие асимптотической сложности.

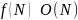
Асимптотическая сложность – функция сложности при большом размере входных данных.

Классы сложности

1. Алгоритмы с полиномиальной сложностью – функция сложности

F ( n) = 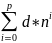, p –порядок сложности (алгоритмы с линейной сложности). Если объем входных данных увеличивается в 2 раза, то и сложность увеличивается в 2 раза.

P=1 -> F(N) ~ N

P = 2 -> F(N) ~ N² – квадратичная сложность

P = 3 -> F(N) ~ N³ – кубическая сложность

2. Алгоритмы с экспоненциальной сложностью - F(N) ~ a^N из математики известно, что экспонента растет быстрее, чем полином любой степени. Можно реализовать, только при маленьком объеме данных. Реализовать такие алгоритмы невозможно.

Возникает задача упрощения – снижения выч. сложности

Существует теория сложности алгоритма

Есть проблема, основная проблема теории сложности – возможно ли произвольный алгоритм с экспоненциальной сложности преобразовать с полиномиальной сложности. Перед тем как упростить алгоритм, нужно провести анализ его выч сложности. 2 способа: подсчет операций и найти оценку выч сложности с помощью рекуррентных соотношений.