
книги фх / Основы химической кинетики
.pdfПодставим (12.8) |
в |
(12.5), |
раскладывая |
в ряд Тейлора |
||
ln(1 ), ln(1+ ) – |
2 |
|
3 |
... , |
и преобразуем, |
удерживая лишь |
|
2 |
|
3 |
|
|
|
главные слагаемые. Получим
k3 2 k1 2 C1 O( 3 , 3 ) – уравнение эллипса.
При удалении от стационарной точки в данном случае также наблюдаются замкнутые траектории в фазовой плоскости, что говорит о положительном изменении, но колебания М1 и М2 будут релаксационные.
12.2. Метод линеаризации
Рассматривая поведение в окрестности стационарной точки, исследование обычно проводят методом линеаризации, так как получить интеграл типа (12.5) или (12.6) удается не всегда. Используем уже рассмотренную систему (12.2'), (12.3').
Находим стационарную точку (их может быть несколько):
k1 A0M1 k2 M1M2 0 |
(M10,M20). |
|||||||
k |
M M |
2 |
k A M |
2 |
0 |
|||
|
2 |
1 |
3 |
0 |
|
|
||
Исследуем поведение системы (12.2'), (12.3') в окрестности стационарной точки. Для этого переменные M1 и M2 записываем в виде (12.8):
M1 |
(t) M10 |
(1 ) k3 A0 (1 (t)) |
|
|
|
|
|
|||
|
|
|
|
k2 |
, |
|
, |
|
1. (12.8') |
|
|
|
|
|
|
|
|||||
|
|
|
|
k1 A0 |
|
|
|
|||
M2 |
(t) M20 |
(1 ) |
(1 (t)) |
|
|
|
|
|
||
|
|
|
|
|
|
|||||
|
|
|
|
k2 |
|
|
|
|
|
|
Подставим (12.8') в систему (12.2'), (12.3') и преобразуем полученное выражение с учетом малости и :
k3 A0 |
k3 A0 |
|
k3 A0 |
|
k1 A0 |
|
k2 k1A0 |
k2 |
(1 ) k2 |
k2 |
(1 ) |
k2 |
(1 ) , |
71
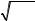
|
k1 A0 |
k |
|
|
k3 A0 |
(1 ) |
k1A0 |
(1 ) k |
A |
k1 A0 |
(1 ) . |
||||||
|
k2 |
|
|
|
|
|
|||||||||||
|
|
2 k2 |
|
|
|
|
k2 |
3 0 k2 |
|
|
|||||||
Разделим первое уравнение на |
k3 A0 , а второе – на |
k1 A0 |
, и после |
||||||||||||||
|
|||||||||||||||||
преобразования получим |
|
|
k2 |
|
|
|
|
k2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
) k A ( ) |
|
|
|
|
|||||
|
|
k A (1 |
|
|
|
|
|||||||||||
|
|
|
|
|
1 0 |
|
|
1 0 |
|
|
. |
|
|
|
|||
|
|
|
k A (1 ) k A ( ) |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
3 0 |
|
|
3 0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Из полученной системы удерживаем только главные линейные
слагаемые, а слагаемые со вторым порядком малости O( , ) отбрасываем. Получаем линеаризованную систему
|
|
|
|
|
|
|
k A |
|
|
||||
|
|
1 |
0 |
|
. |
(12.9) |
|
|
k A |
||||
|
|
|
||||
|
3 |
0 |
|
|
|
|
|
|
|
|
|
||
Для решения системы (12.9) продифференцируем второе уравнение по времени
|
|
2 |
. |
|
k3 A0 k1k3 A0 |
|
|||
Получаем уравнение колебаний |
|
|
|
|
k k A2 0 |
|
|
||
1 |
3 |
0 |
|
|
с частотой колебаний k1k3 A0 . |
|
|
||
Решение этого уравнения имеет вид |
|
|
||
C1 cos t . |
(12.10) |
|||
С1 и φ – константы интегрирования, которые находятся из начальных условий. Пусть начальные условия 0 , 0 . Тогда
(0) 0 , (0) 0 . Из (12.10) находим 0 , C1 0 .
В окрестности стационарной точки ведет себя следующим
образом: |
|
(t) 0 cos t . |
(12.10’) |
Имеем незатухающие гармонические колебания в окрестности центра. Из (12.9) находим
72

(t) |
(t) |
|
0 |
sin t |
k1 |
|
cos |
|
t |
. |
||
k |
A |
|
k |
|
||||||||
|
|
k A |
0 |
|
|
2 |
|
|||||
|
|
3 0 |
|
3 0 |
|
3 |
|
|
|
|
|
|
Используя (12.10') и (12.11), получаем
|
2 |
|
k3 |
|
2 |
|
|
2 |
|
|
|
, |
|||||
|
|
|
k1 |
|
|
|
|
0 |
т.е. имеем уравнение эллипса |
|
|
|
|
|
|||
|
|
|
|
2 |
||||
|
2 |
|
2 |
|
||||
|
k |
k |
|
k |
0 . |
|||
|
|
|
|
3 |
||||
|
|
3 |
|
1 |
|
|
||
(12.11)
(12.12)
В соответствии с (12.12) в фазовой плоскости получили эллипс с
соотношением полуосей k3 и с центром в точке = 0, = 0: k1
0
0 M0 (M10 , M20 ) .
В физическом пространстве при этом, согласно (12.10') и (12.11), имеют место гармонические колебания реагентов M1 и M2 в окрестности их стационарных значений. Частота колебания
k1k3 A0 зависит от констант скоростей первой и третьей ста-
дий и от начальной концентрации исходного вещества. По фазе
колебания M1 опережают колебания M2 на величину /2. Соотношение амплитуд колебаний и определяет отношение констант ско-
ростей k1 и k3. Если k1 > k3, то Am(M1) > Am(M2), и наоборот (Аm – амплитуда). По типу стационарная точка (12.7) является центром.
Следует заметить, что данные колебания и решения (12.10'), (12.11) имеют место лишь в окрестности стационарной точки, пока
и малы. Если система находится вдали от стационарной точки, то колебания будут уже не гармонические, а релаксационные.
Концентрационные колебания во многом аналогичны колебаниям численности популяций в биологических системах. Например, в конце XIX в. в Италии В. Вольтерра была поставлена следующая задача. Имеется местность, в которой отсутствует миграция и в которой проживают хищники – рыси и жертвы – зайцы.
73

Растительная пища в избытке. Вопрос: могут ли рыси съесть всех зайцев? Эта задача аналогична (12.2'), (12.3'), где A0 – растительная пища (в избытке); M1 – численность зайцев, M2 – численность рысей. В результате за несколько десятков лет наблюдений можно было проверить решение этой задачи.
12.3. Схема Лотки–Вольтерра
Эта схема является вторым примером колебательного режима. Процесс включает в себя три стадии:
1)k1 : A M1 ,
2)k2 : M1 M2 M2 ,
3)k3 : M2 P .
Впервой стадии из вещества А образуется промежуточный про-
дукт M1. Во второй из M1 автокаталитически образуется второй промежуточный продукт M2. В третьей стадии M2 распадается на конечный продукт P. Кинетические уравнения имеют вид
dAdt k1 A , dMdt 1 k1 A k2M1M2 ,
dMdt 2 k2M1M2 k3M2 ,
dPdt k3M2 .
Система уравнений имеет первый интеграл, из которого можно найти концентрацию продукта P. Решение будут определять первые три уравнения. Для простоты исследования будем считать A = A0. Тогда поведение системы будут определять уравнения
dM1 |
k A |
k |
M |
M |
2 |
, |
(12.13) |
|
|
||||||||
dt |
1 |
0 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
74

dM2 |
k |
M |
M |
2 |
k M |
2 |
. |
(12.14) |
|
||||||||
dt |
2 |
1 |
|
3 |
|
|
||
|
|
|
|
|
|
|
|
Исследуем (12.13), (12.14) методом линеаризации в окрестности стационарной точки. Найдем стационарную точку
k1A0 k2M1M2 0 ,
k2M1M2 k3M2 0 .
Отсюда получаем одну стационарную точку
M10 k3 , M20 k1 A0 .
k2 k3
Дальше решение ищем в виде
M1 |
|
k3 |
(1 ) , M2 |
|
k1 A0 |
(1 ) , |
|
|
|||||
|
|
k2 |
|
k3 |
||
где , << 1. Подставим (12.16) в (12.13) и (12.14)
|
k3 |
|
|
|
|
|
|
k3 |
|
|
|
k1 A0 |
|
|
|
|
|
|
|
k1A0 |
k2 |
k2 |
(1 |
) |
k3 |
(1 |
), |
|
|||||||
k2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
k A |
|
|
k |
3 |
|
|
|
|
k A |
|
|
|
k |
|
|||
|
1 |
0 |
|
k2 |
|
(1 |
) |
1 |
0 |
(1 ) k3 |
1 |
A0 (1 ). |
|||||
|
k |
3 |
k |
2 |
k |
3 |
k |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||
Из этой системы путем преобразований получаем
|
|
|
k2k1 |
A0 |
11 , |
|
k3 |
||||
|
|
|
|
|
|
|
|
k3 (1 ) . |
|||
|
|||||
Удержим слагаемые только первого порядка малости
|
|
|
k2k1 |
A0 |
, |
|
k3 |
||||
|
|
|
|
|
|
|
|
k3. |
|
|
|
|
|
|
|||
(12.15)
(12.16)
(12.17)
Решим систему (12.17). Продифференцируем первое уравнение
|
k2k1 |
|
k2k1 |
A0 |
|
k2k1 |
|
. |
|
k3 |
A0 ( ) |
k3 |
( k3) |
k3 |
A0 k2k1 A0 |
||
|
|
|
|
|
|
75
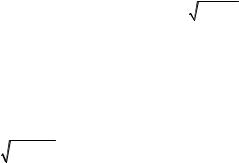
Введем обозначения
2 k2k1 A , k |
2 |
k A . |
||||
k3 |
0 |
0 |
|
1 |
0 |
|
|
|
|
|
|
|
|
Тогда уравнение для примет вид |
|
|
|
|
|
|
|
|
2 |
0 . |
(12.18) |
||
2 0 |
||||||
Полученное уравнение описывает затухающие колебания, где – декремент затухания. Общее решение этого уравнения имеет вид
|
|
|
(t) C e t cos t , |
(12.19) |
|
|
|
1 |
|
где |
2 |
2 |
. Получаем условие колебаний в безразмерном |
|
виде |
0 |
|
|
|
|
|
2 2 . |
|
|
|
|
|
(12.20) |
|
|
|
|
0 |
|
Или, если перейти к размерным переменным:
k |
k A |
|
k |
2k 2 A2 |
, |
||
|
2 |
1 |
0 |
||||
|
2 1 0 |
|
|
4k2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
4k 2 |
k |
2 |
k A . |
(12.20’) |
||
|
3 |
|
|
1 |
0 |
|
|
Таким образом, решение можно записывать в виде (12.19) только в том случае, если выполняется условие (12.20'). Константы С1
и φ определяются из начальных условий (0) 0 , (0) 0 . Начальное условие (0) определим из первого уравнения (12.17):
|
|
|
|
|
|
|
|
|
|
2( |
|
), |
|
|
|
||||
|
|
|
|
|
|
|
|
(0) |
0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
(12.21) |
|
|
|
|
|
|
|
|
|
|
(0) . |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставим (12.19) в (12.21), получим |
|
|
|
|
|
||||||||||||||
2( |
0 |
) |
C |
e t cos t e t sin |
t |
|
|||||||||||||
, |
|||||||||||||||||||
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 0 |
|
0 |
C cos . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно: |
|
|
|
0 |
0 |
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2( |
|
|
) C |
|
cos sin |
|
, |
(12.22) |
||||||
|
|
|
|
|
|
|
C cos. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
76
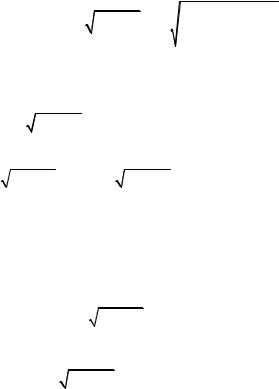
Из последней системы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 1 |
|
|
0 |
|
tg , tg |
|
|
1 |
2 |
0 |
|
. |
|
|
|||||||
|
|
|
0 |
|
|
0 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
С1 получим из второго уравнения (12.22): |
C |
|
0 |
. |
|
|
||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
cos |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда |
1 |
|
1 tg2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
cos2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|
1 tg2 |
|
|
|
2 |
|
|
|
|
|
|
||||
|
C |
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
1 2 |
0 |
|
. |
|||||||
|
|
|
|
|
|
2 |
|
|||||||||||||||||
|
1 |
|
cos |
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Определим выражение для . Из первого уравнения (12.17):
(t) C1 e |
t sin t cos t |
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 e t |
2 |
2 cos cos t |
sin sin |
t , |
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
где cos |
|
|
|
, sin |
|
|
|
|||||
|
|
|
|
|
|
|
. |
|
|
|||
|
2 |
2 |
|
|
2 2 |
|
|
|||||
Угол ψ существует, так как выполняется соотношение |
||||||||||||
|
|
|
|
|
|
sin2 cos2 1 . |
|
|||||
Тогда |
|
|
|
|
|
|
|
tg . |
|
|
||
|
|
|
|
|
|
|
|
|
|
(12.23) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
С учетом последних преобразований |
|
|
||||||||||
|
|
(t) C1e t |
2 |
|
2 cos t . |
|||||||
Получаем в итоге |
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
(t) |
|
|
2 |
2 |
|
C e t cos t , |
(12.24) |
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
1 |
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
где 1 , а ψ определяется из (12.23).
77
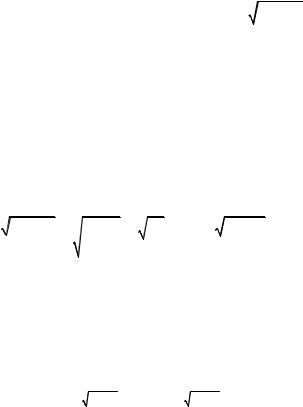
При выполнении условия (12.20') в окрестности стационарной точки (12.16) имеют место затухающие колебания с логарифмиче-
ским декрементом затухания k2k1 A0 . Если декремент затуха- 2k3
ния мал: T << 1, где Т – период колебаний T |
1 |
|
|
1 |
|
|
, то |
||||
|
|
02 2 |
|||||||||
|
|
|
|
|
|
|
|||||
затухание незначительно. При этом |
|
|
1 , |
|
|
1 |
и |
||||
|
|
||||||||||
|
|
|
|
|
|
|
|
||||
tg 1. Тогда |
и |
. Следовательно, коле- |
|
|
2 |
1 |
2 |
|
|||
бания по фазе опережают колебания на угол 1, который при малом декременте затухания близок к /2, т.е. колебания при малом декременте затухания будут почти гармонические с таким же сдвигом по фазе, как и в схеме Вольтерра. По амплитуде колебания и соотносятся как
A |
|
2 |
|
2 |
|
|
2 |
|
2 |
|
2 |
. |
A |
2 2 |
2 |
|
2 |
0 |
k2k1 A0 |
||||||
|
|
|
|
2 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В зависимости от соотношения k1 и k2 а также от начальной концентрации A0 амплитуды могут соотноситься между собой по-
разному. Если декремент затухания мал, то А >> А .
Если условие колебания (12.20') не выполняется, то колебания отсутствуют и в окрестности стационарной точки наблюдается апериодическое движение в сторону стационарной точки так, что
|
|
2 |
0 |
, |
0 , 2 0 |
||||
(t) C e 02 2 t |
C |
e 02 2 t , |
||
1 |
2 |
|
|
|
где С1, С2 находятся из начальных условий. Аналогичный вид име-
ет выражение для (t).
Стационарная точка (12.15) при выполнении условия (12.20') является стационарной точкой типа устойчивый фокус. Тогда в
78
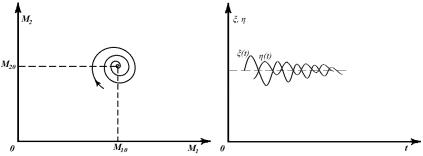
фазовом и физическом пространстве будем наблюдать картину, указанную на рис. 11.
Рис. 11. Фазовые траектории. Стационарная точка типа устойчивый фокус
В случае невыполнения (12.20') стационарная точка является стационарной точкой типа устойчивый узел (см. рис. 10).
79
13. ЭЛЕМЕНТАРНЫЕ ПОНЯТИЯ ТЕОРИИ ЦЕПНЫХ РЕАКЦИЙ
Цепные реакции – это сложные химические процессы, в которых превращение исходных веществ в продукты осуществляется путем регулярного чередования нескольких реакций со свободными радикалами.
Свободный радикал – это часть молекулы, имеющая на внешней электронной орбите неспаренные электроны (наличие свободной валентности), в результате чего они активны в химическом отношении.
Свободные радикалы, которые участвуют в цепной реакции, называются активными центрами цепной реакции, потому что они ведут цепной процесс. В начальной стадии свободными радикалами часто выступают свободные атомы (H, N, Cl и т.д.).
При прохождении цепной реакции различают следующие стадии цепного процесса:
1. Стадия зарождения цепей – стадия цепной реакции, приводящая к образованию свободных радикалов. Механизмы могут быть различными:
1)образование цепей, т.е. возникновение свободных радикалов из молекул исходных веществ в результате их молекулярного распада или их бимолекулярного взаимодействия;
2)зарождение цепей может происходить на стенках реакцион-
ного сосуда;
3)образование свободных радикалов может происходить также
врезультате посторонних воздействий на систему. В этом случае
процесс зарождения цепей принято называть инициированием.
Примеры инициирования:
Часто имеет место фотохимическое инициирование (под воздействием света). Так, например, смесь газов H2 и Cl2 при обычных условиях долго хранится, не реагируя. Если на нее подействовать светом, то произойдет взаимодействие
80
