37. Оценка генеральной средней по выборочной средней.

Генеральной средней   называют среднее арифметическое значений признака X генеральной совокупности.

Если значения   различны, то

 .

Выборочной средней   называют среднее арифметическое значений признака выборочной совокупности.

Если   различны, то

Если имеют соответственно частоты   , причём   , то

 (2)

Оценка генеральной средней по выборочной средней заключается в использовании выборочной средней для приближения к истинному среднему значению генеральной совокупности. 12

Выборочная средняя — это среднее значение, рассчитанное по подмножеству генеральной совокупности, которое называется выборкой. Так как выборка является лишь частью всей совокупности, выборочная средняя используется для оценки генеральной средней. 1

Чем больше объём выборки, тем точнее выборочная средняя отражает генеральную. 13

Для оценки точности выборочной средней применяются стандартная ошибка и доверительные интервалы. Стандартная ошибка показывает, насколько выборочная средняя может отклоняться от генеральной, а доверительный интервал указывает диапазон, в котором с определённой вероятностью находится истинная генеральная средняя. 1

38. Групповая и общая средние.

Допустим, что все значения количественного признака X совокупности, безразлично-генеральной или выборочной, разбиты на несколько групп. Рассматривая каждую группу как самостоятельную совокупность, можно найти ее среднюю арифметическую.

Групповой средней называют среднее арифметическое значений признака, принадлежащих группе.

Общей средней   называют среднее арифметическое значений признака, принадлежащих всей совокупности. Зная групповые средние и объемы групп, можно найти общую среднюю: общая средняя равна средней арифметической групповых средних, взвешенной по объемам групп.

Пример. Найти общую среднюю совокупности, состоящей из следующих двух групп:

Группа первая вторая

Значение признака ... 1 6 1 5

Частота 10 15 20 30

Объем 10+15 = 25 20+30=50

Решение. Найдем групповые средние:

;

Найдем общую среднюю по групповым средним:

Замечание. Для упрощения расчета общей средней совокупности большого объема целесообразно разбить ее на несколько групп, найти групповые средние и по ним общую среднюю.

39. Отклонение от общей средней и его свойство.

40. Генеральная дисперсия. Выборочная дисперсия.

Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.

Генеральной дисперсией D_г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения  .

Если все значения x₁, х₂, ..., x_N признака генеральной совокупности объема N различны, то

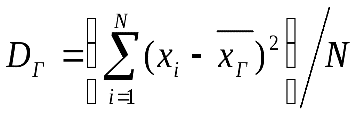
Если же значения признака х₁, х₂, ..., x_k имеют соответственно частоты N₁, N₂, ..., N_k причем N₁+N₂+...+N_k=N, то

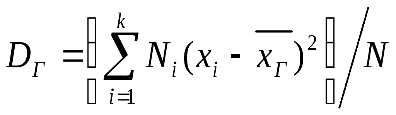
т.е. генеральная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.

Для того чтобы охарактеризовать рассеяние: наблюдаемых значений количественного признака выборки вокруг своего среднего значения  , вводят сводную характеристику — выборочную дисперсию.

Выборочной дисперсией D_B называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения  .

Если все значения x₁, х₂, ..., x_n признака выборки объема n различны, то

Если же значения признака х₁, х₂, ..., x_k имеют соответственно частоты n₁, n₂, ..., n_k причем n₁+n₂+...+n_k=n, то

т.е. выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.