МАТЕМАТИКА ЭКЗАМЕН

1. Предмет и основные понятия теории вероятностей (случайный эксперимент, пространство элементарных исходов, случайное событие).

2. Операции над случайными событиями. Несовместные события. Достоверное, невозможное, противоположное события.

3. Статистическое, классическое и геометрическое определение вероятности.

Геометрическая вероятность, то есть вероятность попадания точки в некоторую область, отрезок, часть

плоскости.

Геометрической вероятностью события A называют отношение меры области, благоприятствующей появлению события A, к мере всей области.

где mes ‒мера (длина, площадь, объём области).

Классическое определение вероятности: вероятностью события А называется отношение

числа m благоприятствующих этому событию исходов к общему

числу n всех равновозможных несовместных элементарных исходов, образующих полную группу:

4. Аксиомы теории вероятностей. Вероятность противоположного события и разности событий. Теорема сложения вероятностей.

5. Условная вероятность. Независимость событий. Теорема умножения вероятностей.

6. Полная группа событий. Формулы полной вероятности и Байеса.

Если событие А может произойти только при выполнении одного из

событий , которые образуют полную группу несовместных событий,

то вероятность события А вычисляется по формуле

.

Эта формула называется формулой полной вероятности.

Если событие А произошло, то это может изменить вероятности

гипотез .

По теореме умножения вероятностей

,

откуда

.

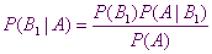Аналогично, для остальных гипотез

Полученная формула называется формулой Байеса

7. Независимые испытания. Формула Бернулли.

8. Случайные величины. Функция распределения и её свойства. Вероятность попадания случайной величины в интервал.

9. Дискретная случайная величина. Ряд распределения и функция распределения дискретной случайной величины.

10. Непрерывная случайная величина. Плотность вероятности и функция распределения непрерывной случайной величины.

Случайная величина называется непрерывной, если множество ее возможных

значений представляет собой некоторый конечный или бесконечный промежуток числовой оси. температура больного в фиксированное время суток,

Одним из возможных способов задания непрерывной случайной величины является

использование с этой целью соотв. функции распределения. Функция F(x), равная вероятности того, что случайная величина Х в результате испытания примет значение , меньше х, называется функцией распределения данной случайной

величины :F(x)=P(X<x)

Плотностью распределения вероятностей (плотностью вероятности) f(x)

непрерывной случайной величины Х называется производная функции распределения F(x) этой величины: f(x)=F’(x)

11. Математическое ожидание случайной величины и его свойства.

Математическое ожидание дискретной случайной величины – это сумма парных

произведений всех возможных ее значений на соответствующие вероятности:

,