матем все лекции

Функция f : X R , X R – непрерывна в точке a X 0 ( ) 0 :

f (S (a) X ) S ( f (a))

(т.е. f (x) S ( f (a)) x S (a) X ).

Д) В более общей форме на языке окрестностей определению непрерывности можно придать следующую форму: Функция f : X R , X R –непрерывна в точке a X для любой окрестности U точки f (a)

существует такая окрестность V точки a , что

f (V X ) U .

Е) С учетом В) и теоремы о равносильности определений предела по Коши и по Гейне, определение непрерывности функции в точке можно сформулировать на языке последовательностей:

lim f (xn ) f (a) .

n

При этом следует иметь в виду, что если точка a X является изолированной точкой множества X , то

существует лишь одна последовательность {xn } X такая, что xn a , а именно стационарная

n

последовательность, все члены которой совпадают с точкой a а для такой последовательности равпенство

lim f (xn ) f (a) , очевидно выполнено

n

Как будет показано далее, каждая элементарная функция является непрерывной в своей области определения, т.е. непрерывной в любой точке своей области определения.

Напомним, что к числу, так называемых, основных элементарных функций относятся:

f (x) x , определенная при x R, если n и определенная при x (0, ), если R \

;

– показательная функция: f (x) a x , x R, a 0 (a const) ;

– обратные тригонометрические функции:

arcsin x , arccos x ( 1 x 1), arctg x, arcctg x (x R) .

В свою очередь, элементарной называется всякая функция, которая может быть получена из основных элементарных функций с помощью конечного числа арифметических операций и образования суперпозиций.

Как будет показано далее каждая элементарная функция является непрерывной в любой точке своей области определения.

Следующие теоремы вытекают из аналогичных теорпем о пределе функции

Теорема 1 (О непрерывности сужения). Пусть функция f : X R непрерывна в точке x0 X и E X причем x0 E . Тогда функция f | E также непрерывна в точке x0 .

Д о к а з а т е л ь с т в о непосредственно вытекает из определения сужения и определения

непрерывности.

Отметим еще ряд теорем, которые с учетом замечания в) вытекают из аналогичных теорем о пределе функции.

Теорема 2 (Арифметические свойства непрерывных функций). Пусть функции f и g определены на множестве X R и непрерывны в точке x0 X . Тогда и функции:

непрерывна в точке x0 X . Тогда существует такая окрестность V точки x0 , что функция f ограничена на множестве V X .

Теорема 4 (О стабилизации знака). Пусть функция f определена на множестве X и непрерывна в точке x0 X . Тогда если f (x0 ) 0 , то существует такая окрестность V точки x0 , что

signf (x) signf (x0 ) x X V .

Наконец отметим еще две простые теоремы

Теорема 5. Пусть функция g определена на множестве Y R и непрерывна в точке y0 , а

Д о к а з а т е л ь с т в о приводится на лекции.

Пусть функция f определена на множестве X R и a X . Рассмотрим множества:

Замечание. На языке " " , например, определение непрерывности слева, формулируется следующим

образом: функция f : X R называется непрерывной слева в точке a X , если 0 ( ) 0 :

| f (x) f (a) |

x X , a x a .

§16. Точки разрыва функции. Классификация точек разрыва.

Определение 1. Пусть функция f определена на множестве X R и a X . Если функция f непрерывна в точке a , то она называется точкой непрерывности функции f . В противном случае, точка a называется точкой разрыва функции f .

Замечание 1. Так как всякая изолированная точка множества X R является точкой непрерывности

определенной на нем функции f , то точками разрыва могут быть только точки сгущения множества X ,

принадлежащие этому множеству.

Увы, часто однако вопреки определению 1, к точкам разрыва функции относят и точки, не принадлежащие области ее определения, но в которых существуют оба односторонних ее предела f (a 0) и f (a 0) , при

этом допускается, что оба они или один из них являются бесконечными. Так обычно, точка x 0 считается

предела f (a 0) и f (a 0) существуют и конечны, то точка a называется точкой разрыва 1-го рода,

в противном случае (т.е. если в ней хотя бы один из этих односторонних пределов не существует, либо является бесконечным), она называется точкой разрыва второго рода

Определение 3. Точка разрыва 1-го рода называется точкой устранимого разрыва функции f ,

если в ней существует предел функции f , но он не равен ее значению в этой точке.

Замечание 3. Если точка a – точка устранимого разрыва функции f , то изменив ее значение в этой точке на значение, равное величине предела в этой точке, получим непрерывную функцию g в этой точке:

Этим и объясняется термин точка устранимого разрыва.

что xnr a и xni a n . Таким образом, каждая точка a R – точка разрыва 2-го рода функции Дирихле.

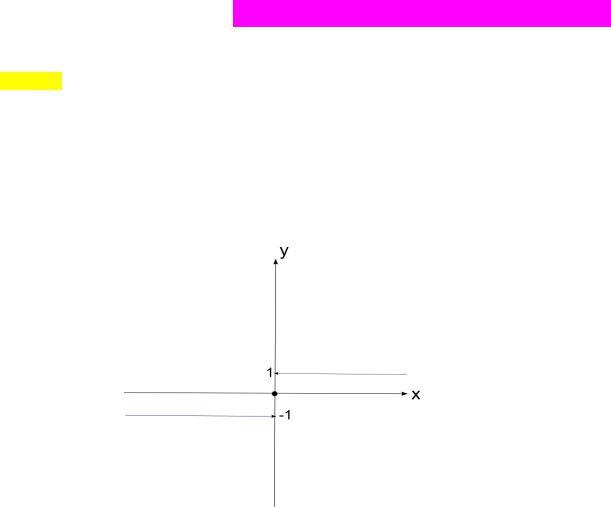
Пример 2. Функция «сигнум x »

1, если x 0 sign x 0, если x 0

1, если x 0

очевидно, разрывна в точке x 0 , причем эта точка – точка разрыва 1-го рода.

Рис. 1 График функции y = sign x.

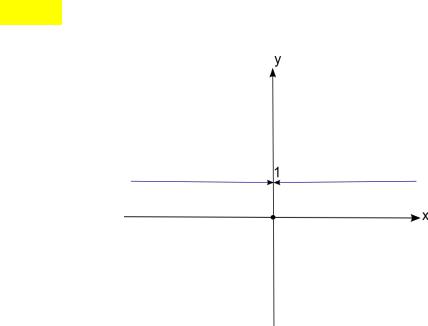
Пример 3. Функция f (x) sign x2 разрывна в точке x 0 , которая, очевидно, является точкой

устранимого разрыва.

Рис. 2 График функции y = sign x2

Замечание 2. Теорема 1 позволяет также установить наличие вещественного корня у всякого многочлена нечетной степени

f (x) a0 x 2n 1 a1 x 2n ... a2n x a2n 1

Действительно, при достаточно больших по абсолютной величине значениях x этот многочлен имеет знак старшего члена, т.е. члена a0 x 2n 1 . Точнее, при положительных таких x он имеет знак, равный знаку a0 , а при отрицательных таких x он имеет обратный знак. Так как

многочлен – непрерывная на всей числовой оси функция, то по теореме 1 хотя бы в одной точке x R он обращается в нуль.

Теорема 2 (вторая теорема Больцано-Коши). Пусть функция f определена и

непрерывна на отрезке [a, b] , причем на концах этого отрезка она принимает разные значения

A f (a) f (b) B .

Тогда каковы бы ни было число C , лежащее между A и B найдется такое c (a, b) ,

что

f (c) C .

Д о к а з а т е л ь с т в о. Пусть для определенности A B . Выберем произвольное C , A C B , и рассмотрим вспомогательную функцию g(x) f (x) C . Она, очевидно,

непрерывна на отрезке [a, b] и на его концах принимает значения разных знаков: g(a) f (a) C A C 0, g(b) f (b) C B C 0 .

По теореме 1 существует такое c (a, b) , что g(c) 0 , т.е. f (c) C 0 или f (c) C □

Следствие. Если функция f определена и непрерывна на конечном или бесконечном промежутке X a, b , то множество ее значений Y f ( X ) также