матем все лекции

Для обозначения того, что b – предел последовательности {yn }пишут

lim yn b (а также, короче lim yn b)

n

или

yn b +

Опираясь на определение бесконечных пределов функции (пределов равных или )

легко сформулировать аналогичные определения и для последовательности. Читателю предлагается это сделать самостоятельно.

О п р е д е л е н и е 2. Если числовая последовательность имеет конечный предел, то говорят, что она сходится и называют ее сходящейся. В противном случае, т.е. если она не имеет предела вовсе или имеет бесконечный предел, говорят, что она расходится и

называют ее расходящейся.

Замечание 1. В силу того, что числовая последовательность является в то же время и числовой функцией

– из теоремы о единственности предела числовой функции следует, что сходящаяся числовая последовательность имеет только один предел (очевидно, и бесконечный предел у числовой последовательности может быть только один или или );

– теорема о стабилизации знака, теорема о предельном переходе в неравенстве, теорпема о двойном неравенстве (принцип двух полицейских), теорема об арифметических свойствах предела при надлежащей переформулировке справедливы и для числовых последовательностей;

– естественным образом формулируются понятии б.м. и б.б. числовой последовательности, сохраняются их свойства и связь между ними;

Замечание 3. Вместе с тем для последовательностей вместо теоремы о локальной ограниченности функции имеющей (конечный) предел справедлива следующая более сильная теорема (о глобальной ограниченности). Предварительно напомним, что функция (в частности числовая последовательность) называется ограниченной если мн-во ее значений ограничено, а тогда с учетом критерия ограниченности числового мн-ва можно сказать, что числовая

последовательность {yn } ограничена С 0 : | yn | С n

Теорема 1. Всякая сходящаяся числовая последовательность ограничена.

Следующий пример показывает, что утверждение обратное к утверждению последней теоремы, вообще говоря, неверно, т.е. ограниченная последовательность необязательно является сходящейся.

принадлежать -окрестности S (a) (a , a ) , так как расстояние между точками a и a меньше двух, а расстояние между точками 1 и 1 равно двум.

Рассмотрим еще один важный пример. Предварительно отметим, что для любого вещественного числа x существует такое целое число px , что

px x px 1.

Очевидно, такое целое число единственное для любого x R . Оно называется целой частью числа x и обычно обозначается [x].

Пример 2. Пусть q - некоторое вещественное число. Рассмотрим последовательность

{x } ,

n n 1

Если q 1, то xn 1 n 1, 2,... , т.е. последовательность (4) стационарная и, следовательно, lim xn 1.

Если же q 1 , то рассматриваемая последовательность та же, что и в предыдущем примере. Следовательно, если q 1 , то последовательность (4) расходится.

n N очевидно будем иметь | qn | . Следовательно в рассматриваемом случае (т.е. когда | q | 1)

б) при | q | 1 и q 1 последовательность (4) расходится.

§ 8. Символы «о» и «О». Эквивалентные при x a функции.

Пусть функции f и g определены на множестве X R и a R – точка сгущения

множества X . Пусть также в некоторой проколотой окрестности V точки a функция g отлична от

ограниченности функции, имеющей предел, f (x) O(g(x)) при x a .

Замечания 3. В силу предыдущего замечания заключаем, что если f (x) o(g(x)) при x a , то тем более f (x) O(g(x)) при x a .

Замечания 4. Как следует из определений 1 и 2, соответственно, запись f (x) o(1) (при x a ) означает, что функция f – бесконечно малая при x a , а запись f (x) O(1) (при x a ) означает, что функция f ограничена в окрестности точки a .

Определение 3. Пусть f и g – б. м. при x a функции и f (x) o(g(x)) при x a .

Тогда ф–я f называется бесконечно малой высшего порядка по сравнению с функцией g .

Определение 4. Бесконечно малые при x a функции f и g называют

По аналогии с определениями 3 и 4 вводятся следующие определения для бесконечно больших функций.

Определение 5. Пусть f и g – бесконечно большие при x a функции. Функция f

называется бесконечно большой высшего порядка по сравнению с функцией g , если f ( x ) g ( x ) – бесконечно большая при x a функция, т.е. если g(x) o( f (x)) при x a .

Определение 6. Пусть f и g – бесконечно большие при x a функции. Если

f ( x) 1 g( x) x a

то говорят, что они эквивалентны при x a .

Замечание 4. Теоремы 1 при надлежащих изменениях сохраняет свою силу для бесконечно больших

функций.

§9. Первый замечательный предел.

Покажем, что

(первый замечательный предел),

т.е., что

sin x ~ x ( x 0 ).

Так как функция sin x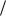 x – четная, то достаточно найти правосторонний ее предел в точке x 0 .

Пусть x (0, 2) . Тогда как видно из следующего рисунка

.

.

.

.