Добавил:

Y-FT-WE Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный технологический институт (технический университет)

Предмет:

Математика

Файл:

матем все лекции

.pdf

Скачиваний:

Добавлен:

14.01.2025

Размер:

9.39 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1714 15 16 17 > Следующая >>>

ЛЕКЦИЯ 1.21

§11. Формула Тейлора.

n.1. Формула Тейлора для многочлена.

Рассмотрим некоторый	многочлен	степени		n	с вещественными
коэффициентами:
p(x) a0	a1 x ... an xn	(an	0)		(1)
Зададим произвольное вещественное число x0			и в правой части равенства (1)
представим x в виде x [(x x0 ) x0 ]:

p(x) a0 a1[(x x0 ) x0 ] ... an [(x x0 ) x0 ]n

Раскрыв здесь квадратные скобки и приведя подобные члены при одинаковых степенях (x x0 ) , в результате получим разложение многочлена (1) по степеням

(x x0 ) :
p(x) b0	b1 (x x0 ) ... bn (x x0 )n ,	(2)
где bk (k 0,1,..., n) - постоянные, зависящие от исходных коэффициентов		и от числа

x0 .

При больших n , на практике, указанный выше способ разложения многочлена по степеням (x x0 ) весьма трудоемок. Имеется более простой способ отыскания

коэффициентов bk (k 0,1,..., n) разложения многочлена по степеням (x x0 ) . Будем последовательно дифференцировать равенство (2):

Примечания

Эта и следующая лекции содержат ответ на

(В.27)

p (x) b 2b (x x		0	) 3b (x x			0	)2			...
1	2	0		3		0
p (x) 2b 3 2b (x x			0	) 4 3b (x x						0	)2	...
2	3		0		4					0
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
p(k ) (x) k!b (k 1)k...2b					(x x			0	) ...
	k			k 1				0

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

p(n) (x) n!bn .

Полагая в каждом из этих равенств x x0 получим

b1		p (x0 )
b1	1!
	1!
b2	p(2)		(x )
b2				0
				0
	2!

. . . . . . . . .

p(k ) (x ) bk k! 0

. . . . . . . . .

		bn		p(n)	(x )
		bn				0
						0
				n!
	Если кроме того положить x x		0	в (2), то считая, как обычно,			p(0) (x)
	Если кроме того положить x x			в (2), то считая, как обычно,			p(0) (x)

0! 1	будем также иметь
		b0		p(0)	(x )
		b0				0
				0!

p(x) и

Таким образом, для коэффициентов разложения (2) многочлена по степеням имеем следующие формулы

	p	(k )	(x0 )		(3)

b				, k 0,1,..., n

k		k!

В итоге заключаем, что разложение (2) можно записать в виде:

p( x) p(x0 )

p (x

)

( x x0 )

p (x

)

( x

x0 )2

...

p(n ) ( x

)

(x x0 )n

(4)

p(k ) (x

)

короче, p( x)

( x

)(k )

k 0

Формула (4) называется формулой Тейлора в точке x0 для многочлена p(x)

степени n . Из вывода этой формулы следует, что разложение многочлена по степеням (x x0 ) является единственным, так как коэффициенты любого такого разложения однозначно определяются по формулам (3).

Формулу Тейлора для многочлена p(x) в точке x0 0 , то есть формулу

(k )

p(x)

(0)

k 0

называют также формулой Маклорена.

n.2. Локальная формула Тейлора.

Пусть функция

f n раз дифференцируема в точке x0 . Напомним, это означает,

что существует такая окрестность V точки x0 , в которой определена сама функция f

существуют конечные производные

f (x), f (x),..., f (n 1) (x)

(x V )

при этом в точке x

существует также конечная производная

f (n) (x

) . Поэтому,

частности, определен многочлен

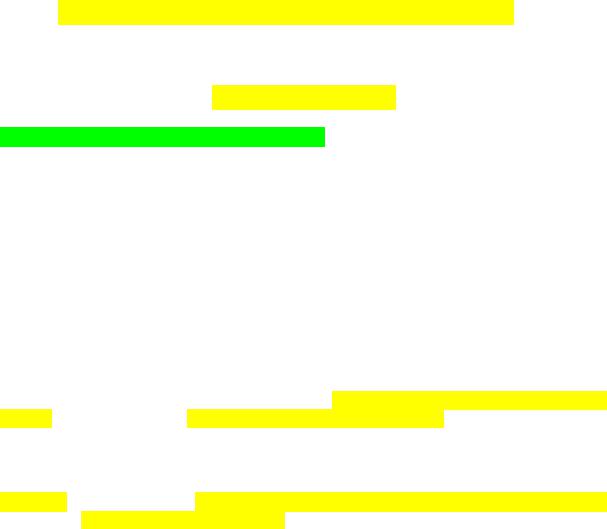
n		(k )	(x0 )
Pn (x0 , x)	f			(x x0 )k ,
		k!
k 0

который называется ( n -ым) многочленом Тейлора функции f в точке x0 . Положим

Rn (x0 , x) f (x) Pn (x0 , x)

Тогда

f (x) Pn (x0 , x) Rn (x0 , x)

Эта формула или, в более явном виде, формула

(k )

(x0 )

(1)

f (x)

(x x0 )k

Rn (x0 , x)

k 0

называется формулой Тейлора

функции f в

точке x0 , а функция Rn (x0 , x) -

остаточным членом формулы Тейлора.

Ниже будет доказано, что остаточный член формулы Тейлора может быть

записан в виде

R (x

, x) o((x x

)n )

(2)

(при x x0 )

Остаточный член в такой форме обычно называют остаточным членом в форме

Пеано, а формулу Тейлора с остаточным членом в такой форме, т. е. формулу

n		(k )			(3)
f (x)	f		(x0 )	(x x0 )k o((x x0 )n )
f (x)		k!		(x x0 )k o((x x0 )n )
k 0		k!

называют, соответственно, формулой Тейлора с остаточным членом в форме Пеано или, также, локальной формулой Тейлора.

	Лемма 1. Пусть функция n раз дифференцируема в точке x0 и
		(x0 ) (x0 ) ... (n) (x0 ) 0 .			(4)
		(x0 ) (x0 ) ... (n) (x0 ) 0 .
Тогда
			(x) o((x x0 )n ) .		(5)
			(x) o((x x0 )n ) .

	Д о к а з а т е л ь с т в о проводится по индукции.
	При n 1 по определению дифференцируемости функции в точке x0			имеем
	(x) (x0 ) (x0 )(x x0 ) o(x x0 )

А так как по условию (4)

(x0 ) (x0 ) 0 ,

то это означает, что

(x) o(x x0 )

таким образом, при n 1 утверждение леммы справедливо.

Предположим, что оно справедливо при n m 1 1, и покажем, что тогда оно справедливо и при n m 2 .

Действительно, поскольку при n m по условию (4)

	( ) (x		0	) ... ( )(m 1) (x	0	) 0
			0		0
то по индукционному предположению для функция имеем
	(x) o((x x0 )m 1 )						(6)
Далее,	так как функция	m раз дифференцируема					в точке x0 и m 2 , то для
любой точки	x из некоторой	окрестности V (x0 , x0					) имеет место формула
конечных приращений Лагранжа
	(x) (x0 ) ( )(x x0 ) ,						(7)

где точка (x) лежит между точками x			и x0 . Но так как (x0 ) 0 , то из формул (6)
и (7) следует, что
(x) ( )( x x ) o(( x )m 1 )(x x )				o(( x		0		)m 1 )	(x x )m
(x) ( )( x x ) o(( x )m 1 )(x x )				(x x			)m 1		(x x )m
	0	0	0	(x x			)m 1		0
	0	0	0						0
					0
Полагая здесь

(x)	o(( x )m1 )
		0

	(x x	0	)m1

будем иметь

(x) (x)(x x0 )m

Поэтому равенство (5) при n m будет доказано, если будет показано, что

(x) 0

x x0

Действительно, так как точка (x) лежит между точками x и x0 , то

	x0				x x0

и, следовательно,

(x)

o(( x0 )m1 )

( x0 )m1

x x

( x0 )m1

Остаётся заметить, что в силу (9) (x) x0

при x x0 и, значит,

o(( (x) x

)m1 )

( (x) x0 )m1 x x0

Тогда по принципу двух милиционеров из (10) следует (8)

(8)

(9)

(10)

Теорема 1. Если функция f n раз дифференцируема в точке

x0 , то для нее

имеет место формула Тейлора с остаточным членом в форме Пеано (3).

Равносильная

формулировка

Замечание

теоремы 1:

Если функция

f имеет в точке

Д о к а з а т е л ь с т в о.

Достаточно заметить, что при выполнении условий

конечные

производные

до

порядка

теоремы функция

(k )

включительно, то для нее имеет место локальная

(x) Rn (x0 , x) f (x)

(x0 )

(x x0 )k

формула Тейлора (3).

k 0

Удовлетворяет условиям леммы 1

ЛЕКЦИЯ 1.22

§11. Формула Тейлора (продолжение).

nо3. Формула Тейлора с остаточным членом в форме Коши и в форме Лагранжа.

Теорема 2. Пусть функция f и все ее производные до порядка n включительно

являются непрерывными функциями на отрезке I с концами в точках x0 и x , а во внутренних точках этого отрезка существует конечная производная f n 1 (t) порядка n 1 . Тогда, для любой непрерывной на отрезке I функции , дифференцируемой во внутренних точках этого отрезка и имеющей в каждой из этих точек отличную от нуля производную,

существует точка , лежащая между точками x и x0 , такая, что остаточный член в

формуле Тейлора может быть записан в виде

R (x

, x) (x) (x0 )

f (n 1) ( )(x )n .

(1)

n 0

( )n!

Д о к а з а т е л ь с т в о.

На отрезке I с концами в точках x0 и x рассмотрим функцию

переменной t I :

F(t) f (x) Pn (t, x) ,

где

(k )

Pn (t, x)

(t)

(x t)k .

k 0

Из условий теоремы следует, что на отрезке I функция F обладает теми же свойствами, что и функция . Точнее, на отрезке I функции F и удовлетворяют всем условиям теоремы Коши о среднем значении для дифференцируемых функций.

Примечания

См. комментарий к предыдущей лекции

По этой теореме между точками x0 и x найдется такая точка , что

(F(x) F(x0 )) ( ) ((x) (x0 ))F ( )

Поскольку

F(t) f (x) [ f (t)

f (t)

t)2 ...

f (n) (t)

(x t)n ] ,

то нетрудно видеть, что

F (t) [ f (t)

f (t)

(x t)

f (t)

2(x t)

f (t)

(x t)2

...

f (n 1)

(t)

(x t)n ]

f (n 1) (t)

(x t)n .

К тому же, как следует из (3),

F(x) 0

F(x0 ) f (x) Pn (x0 , x) Rn (x0 , x)

Из формул (2), (4) – (6) имеем

Rn (x0 , x) ( ) ((x) (x0 )) f (n 1) (x0 ) (x )n . n!

В свою очередь отсюда, с учетом того, что по условию теоремы ( ) 0 ( - внутренняя точка отрезка I ), получим искомое равенство (1) □

(2)

(3)

(4)

(5)

(6)

Следствие. Если на отрезке с концами в точках x0 и x функция f и все ее

производные до порядка n включительно являются непрерывными функциями, а во

внутренних точках этого отрезка существует конечная производная f (n 1) (t) , то


остаточный член в формуле Тейлора
	n		k			(7)
	f (x)	f		(x0 )	(x x0 ) Rn (x0 , x)
		f		(x0 )
				k!
	k 0			k!
	k 0

может быть записан, как в форме Коши:

R (x

, x)

n 1

( )

(x )n (x x

) ,

(8)

так и в форме Лагранжа:

, x)

(n 1)

( )

(x x

)n 1

(9)

(n 1)!

(здесь лежит между точками x и x0 , при этом является, вообще говоря, разной в формулах (8) и (9)).

До к а з а т е л ь с т в о. Формула (8) вытекает из формулы (1), если в ней положить

(t) x t

Всвою очередь, формула (9) вытекает из той же формулы (1), если в последней положить

(t) (x t)n 1

микаТ образом, если выполнены условия следствия из теоремы 2, то формулу Тейлора

для функции f можно записать как в виде

(k )

(x0 ) (x x0 )k

(n 1)

( )

(x x0 )n 1

(10)

f (x) f

k 0

(n 1)!

(формула Тейлора с остаточным членов в форме Лагранжа),

так и в виде

(k )

(x0 ) (x x0 )k f

(n 1)

( ) (x )n (x x0 )

(11)

f (x) f

k 0

(формула Тейлора с остаточным членом в форме Коши)□

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1714 15 16 17 > Следующая >>>

Соседние файлы в предмете Математика

#
20.01.202510.18 Mб3!ЭКЗАМЕН 2 семестр-1.docx
#
14.01.202510.18 Mб3!ЭКЗАМЕН 2 семестр.docx
#
14.01.20259.39 Mб4матем все лекции.pdf
#
14.01.20253.55 Mб1МАТЕМАТИКА ЭКЗАМЕН.pdf