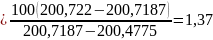Vtoraya

Липецкий государственный технический университет

Кафедра транспортных средств и техносферной безопасности

ПРАКТИЧЕСКАЯ РАБОТА

Обработка полной статистической информации о ресурсе машин

Выполнил: Руководитель:

Студент группы ТК-18-1

Липецк 2019 г.

Практическая работа № 4, 5

Обработка полной статистической информации о ресурсе машин

Методика статистической обработки полной информации

Обработка полной информации содержит следующие этапы :

а) Построение статистического ряда исходной информации и определение смещения начала рассеивания.

б) Определение среднего значения 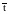ПН и среднего квадратичного отклонения .

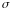в) Проверка информации на выпадающие точки.

г) Построение гистограммы, полигона и кривой накопленных опытных вероятностей.

д) Определение коэффициента вариации V.

е) Проверка совпадения опытных и теоретических законов распределения ПН по критериям соответствия.

ж) Графическое построение интегральной F(t) и дифференциальной f(t) функций ТЗР.

з) Определение доверительных границ рассеивания одиночных и средних ПН и наибольшей возможной ошибки переноса.

Статистический ряд составляют при объеме выборки N ≥ 25 для

упрощения дальнейших расчетов (без потерь точности).

Количество интервалов статистического ряда n определяют по условию n = 8…12.

Длину интервала статистического ряда А рассчитывают по формуле

А = (t _max – t _min) / n,

А= (200,95-200,50)/10=0,045

где t _max и t _min – максимальная и минимальная точки информации соответственно (в курсовой работе это информация об износах) мм.

Смещение начала рассеивания t _см определяют по формуле

t _см = t _1н – 0,5А = 200,5 – 0,5*0,045=200,4775,

где t _1н – начало первого интервала, мм.

Значение опытной вероятности в i –м интервале Р_i определяют по формуле

Р_i = m_i / N,

где m_i – опытная частота i – го интервала.

Полученные данные вносят в таблицу 1.

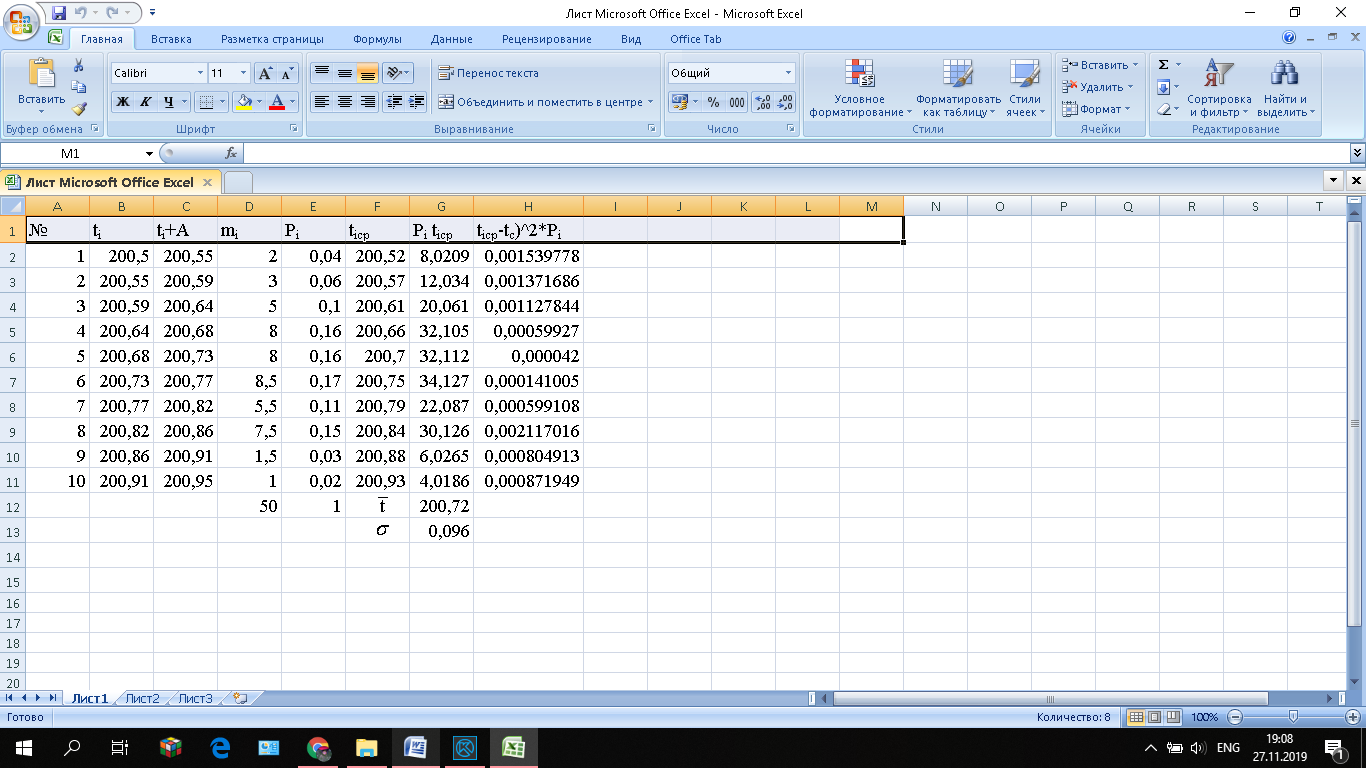
Таблица 1 – Информация об интервалах исходного статистического ряда.

В опытной информации о ПН могут быть ошибочные точки, выпадающие из общего закона распределения. Поэтому перед окончательной математической обработкой информацию проверяют на выпадающие точки по критерию Ирвина

,

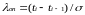
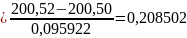где 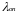– опытное значение критерия Ирвина;

t_i, t_i-1 – смежные точки информации.

Теоретический коэффициент Ирвина 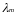определяют по значениям объема выборки N и доверительной вероятности 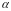, используя таблицу П.1 приложения.

Гистограмма и полигон являются дифференциальными, а кривая накопленных опытных вероятностей – интегральным статистическими законами распределения опытных ПН (рис.1.).

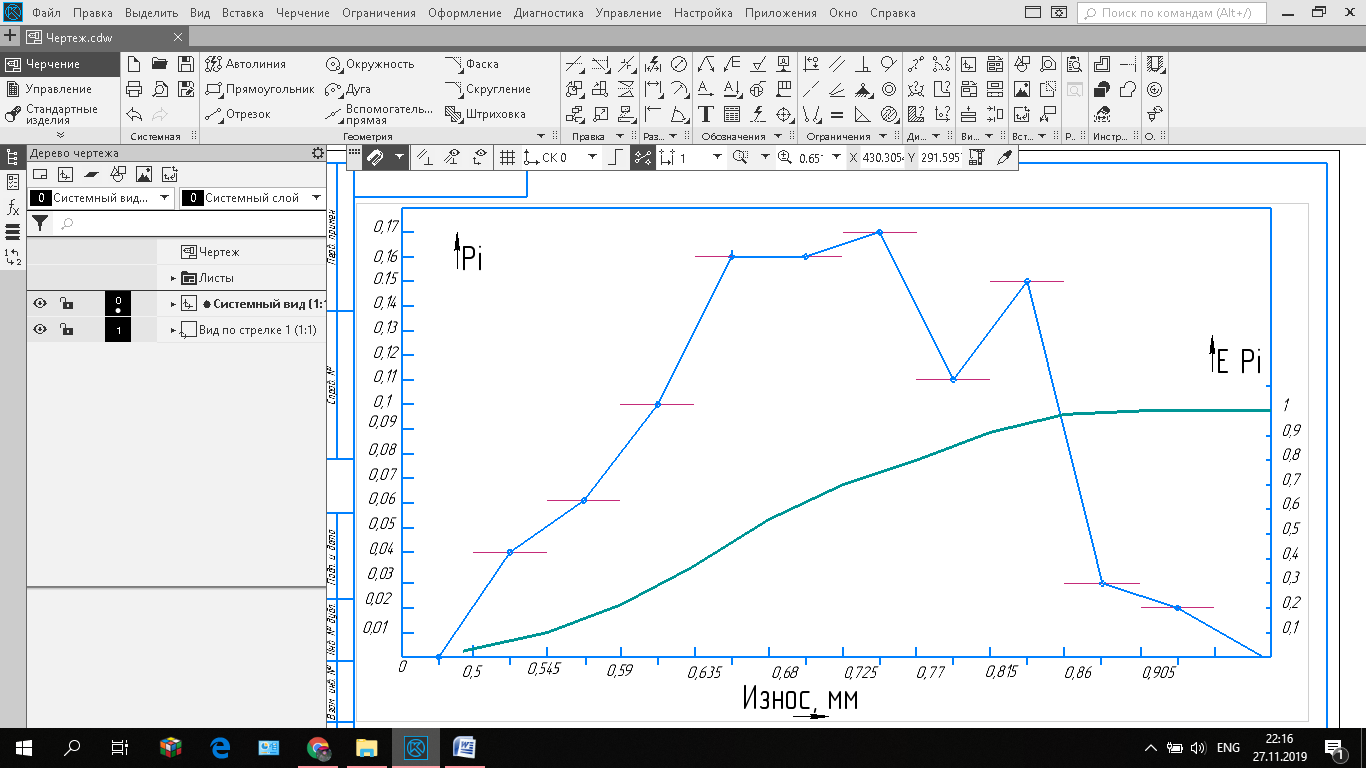
Рисунок 1 – Статистические законы распределения опытных показателей надежности (износ посадочного места под подшипник 7522 в вальцедековом станке СВУ-2):

Коэффициент вариации V является относительной характеристикой рассеивания ПН и используется при предварительном выборе и оценке ТЗР.

Для ПН, зона рассеивания которых начинается от нуля, коэффициент вариации V определяют по формуле

V = 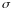/ = 0,095992/ 200,7187= 0,000478

Если зона рассеивания смещена относительна нуля формула имеет вид

V = / ( - t _см) = 0,095992/(200,7187-200,4775)= 0,39797

При V< 0,3 предварительно выбирают закон нормального распределения (ЗНР), если V > 0,5 – закон распределения Вейбулла (ЗРВ).

Критерий согласия Пирсона 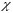² представляет собой сумму квадратов отклонений опытных и теоретических частот в каждом интервале укрупненного статистического ряда информации.

² = 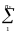(m_i – m_mi)² / m_mi,

где n _y – число интервалов в укрупненном статистическом ряду;

m_i – опытная частота в i – ом интервале укрупненного статистического ряда;

m_mi – теоретическая частота в i – ом интервале укрупненного статистического ряда.

Укрупненный статистический ряд составляют исходя из условий:

n_y 4, m_i 5. Допускается объединение тех интервалов в которых m_i < 5.

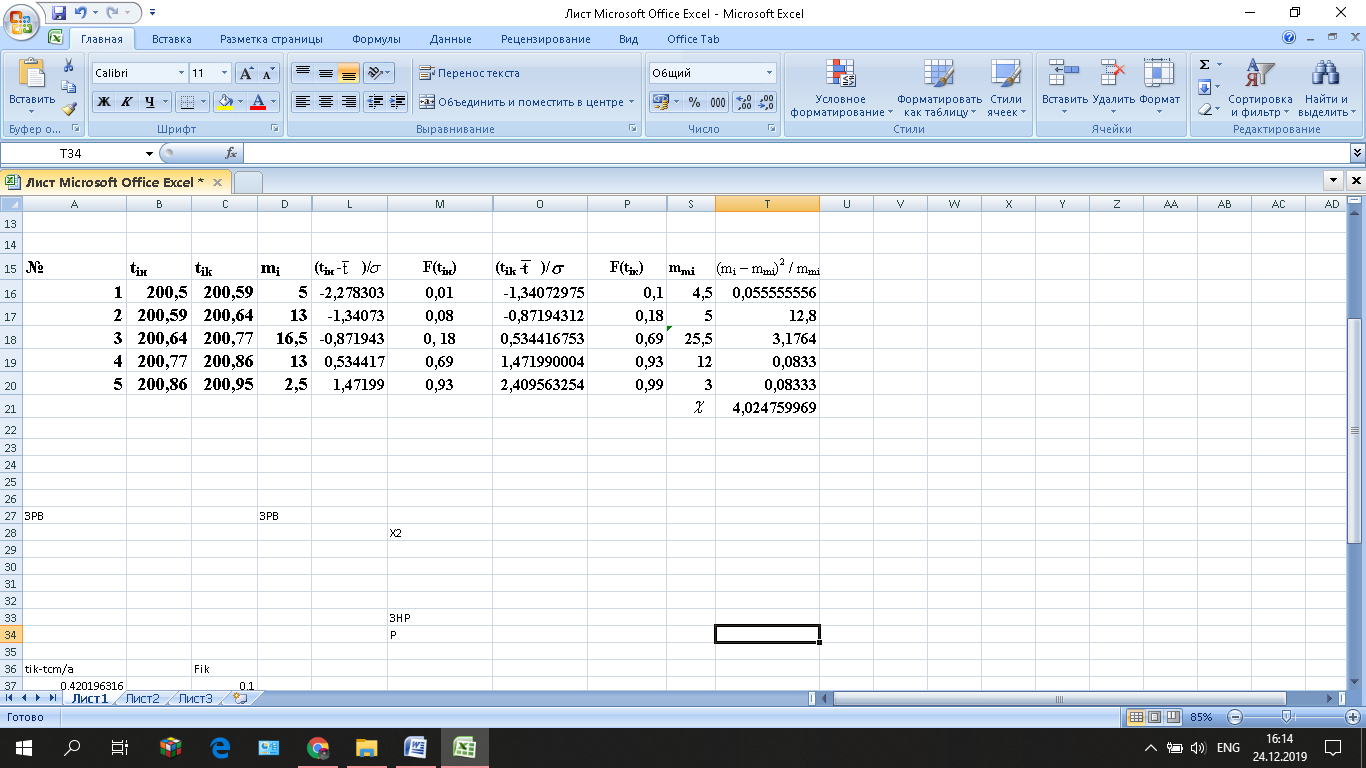
Таблица 2 – укрупнённый статистический ряд. Критерий согласия Пирсона для ЗНР.

Интегральную функцию ЗНР определяют по равенству

F(t _iк) = F_o

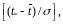
где F_o – центрированная и нормированная интегральная функция, определяемая по табл. П.2. приложения.

Теоретическая частота находится по формуле

m_mi =

Интегральную функцию ЗРВ определяют из табл. П.3. приложения, по величине параметра ЗРВ – b и отношению (t _iк - t _см) / а, где а – параметр ЗРВ.

Параметры а и b можно приближенно рассчитать по формулам

а = 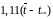= 1, 11(200,7187 – 200,4775 ) = 0,267

b = 1 / V^1,06 = 1 / 0,397^1,06 = 2,65

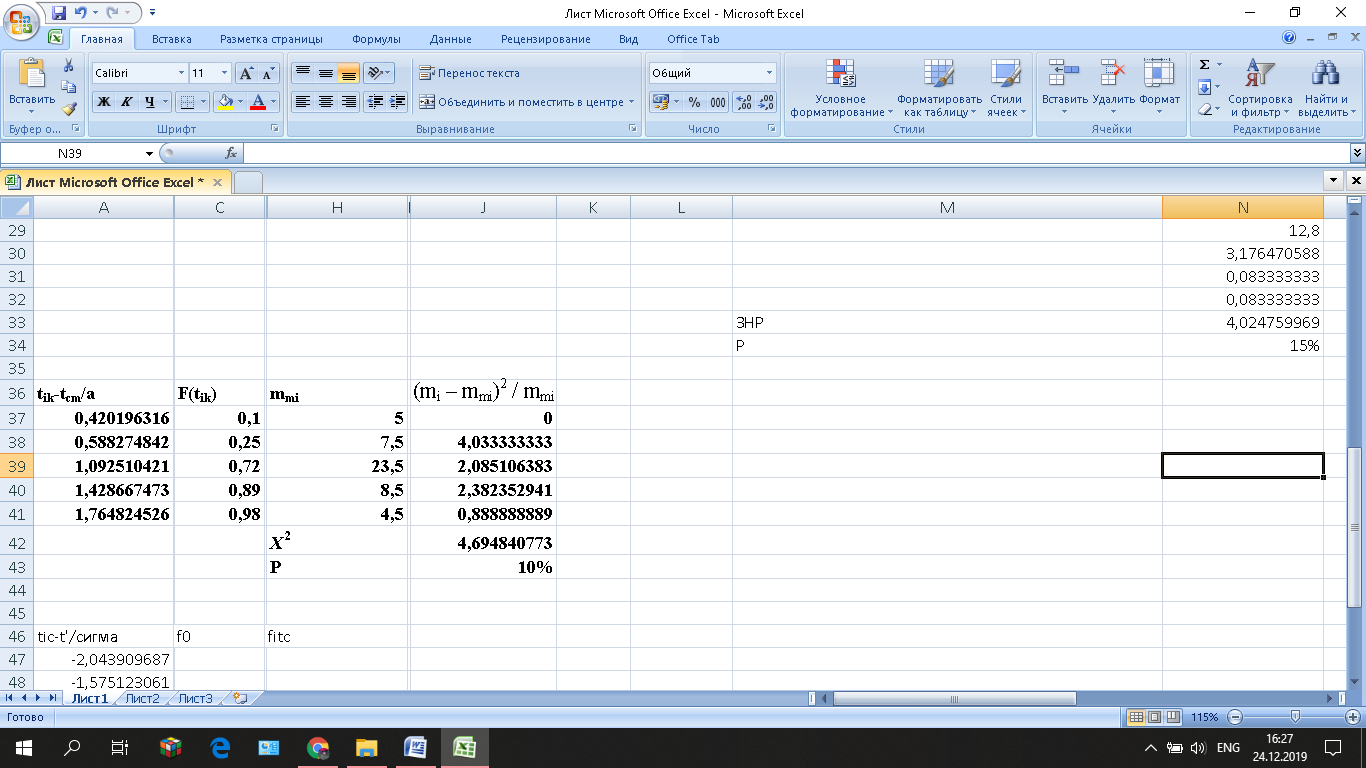
Таблица 3 – интегральная функция ЗНР. Критерий Пирсона для ЗНР.

Рассчитав значения критерия согласия Пирсона ² для ЗНР и ЗРВ, по таблице П.4 приложения, определяют вероятность совпадения опытных и теоретических данных Р. Для входа в таблицу необходимо определить число степеней свободы r по формуле

r = n _y – K = 5-3 = 2,

где К – число обязательных связей. Для ЗНР и ЗРВ число обязательных связей К = 3: две связи это два параметра распределения, а третья связь – 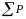= 1,0.

Получаем P для ЗНР – 15%. P для ЗРВ – 10 %.

Выбираем ЗНР.

После окончательного выбора ТЗР рассчитывают значения дифференциальной функции в серединах интервалов исходного статистического ряда f(t_ic).

Для ЗНР по известной формуле

f(t_ic) = (A / ) ,

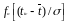где – центрированная дифференциальная функция ЗНР, определяемая по отношению 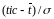в таблице П.5 приложения

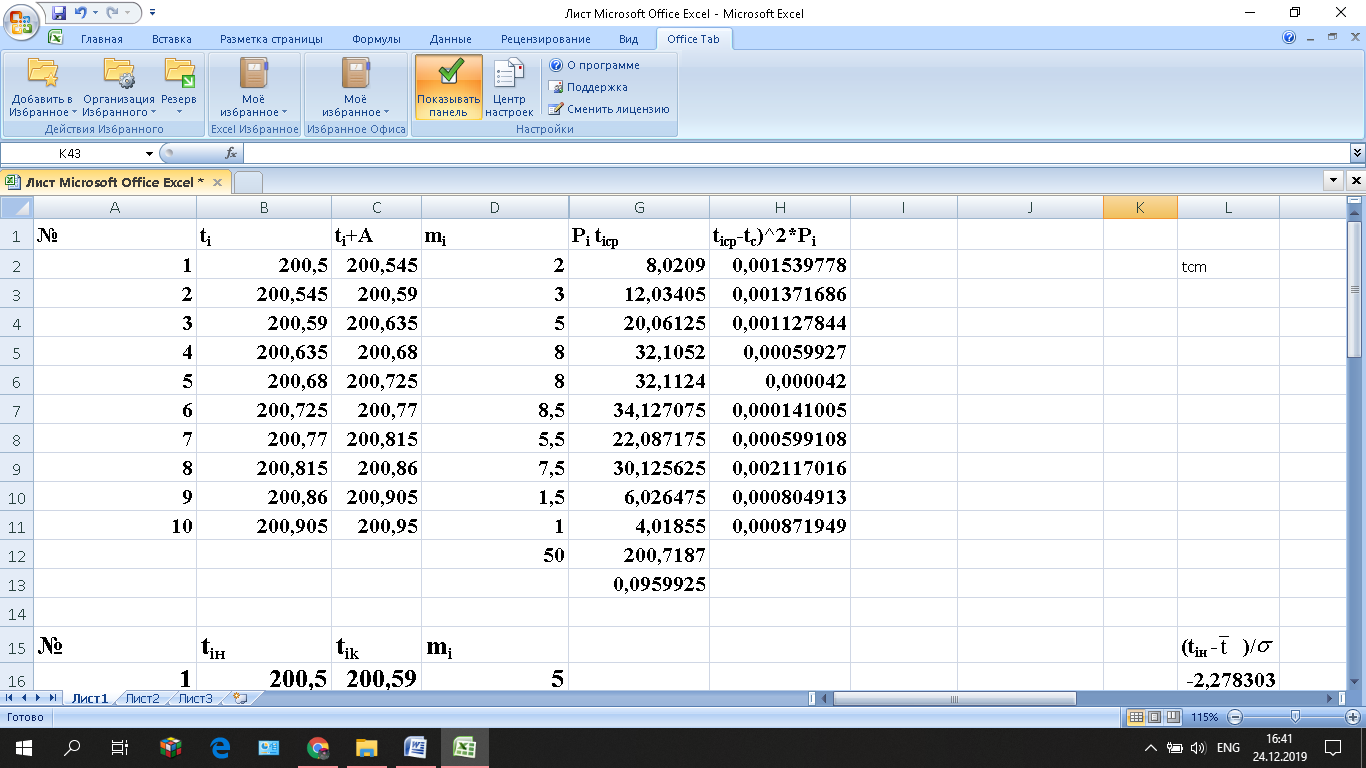
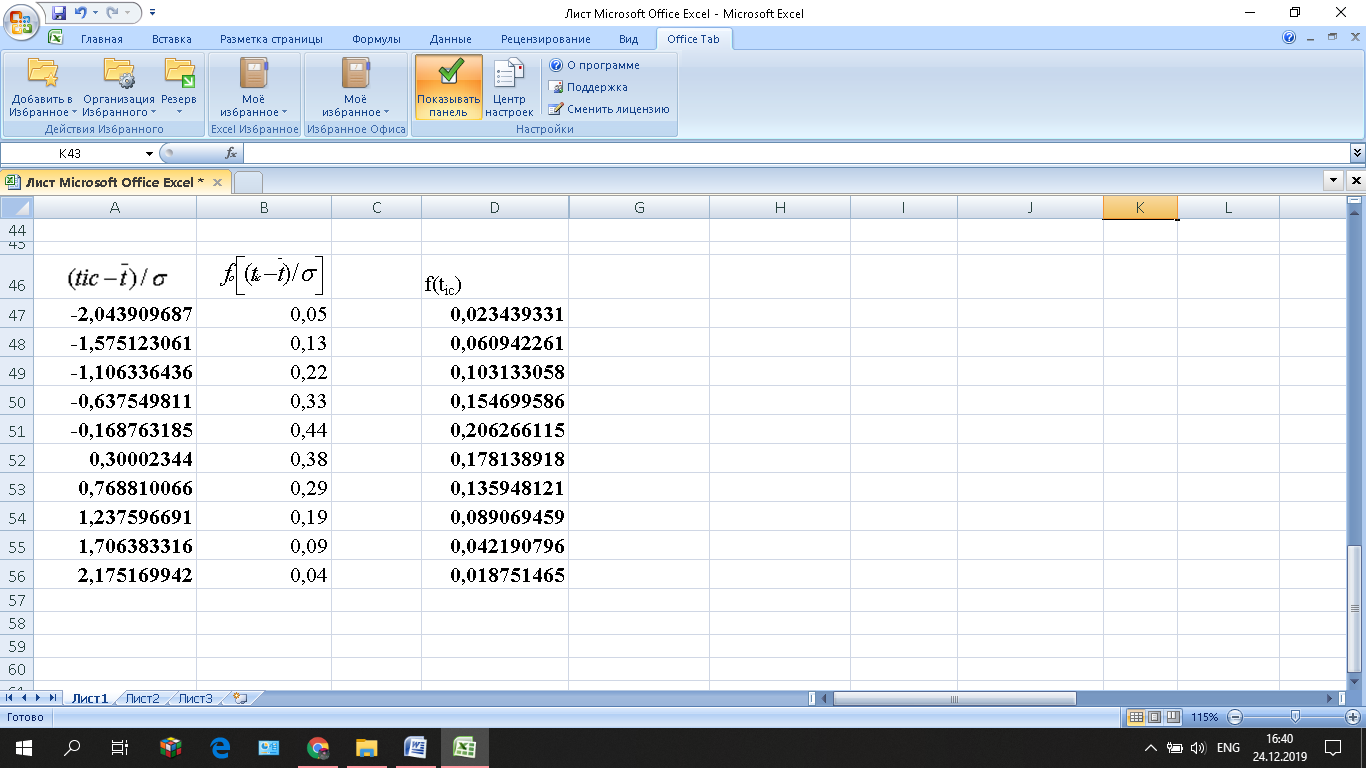
Таблица 3 – дифференциальной функции в серединах интервалов исходного статистического ряда f(t_ic).

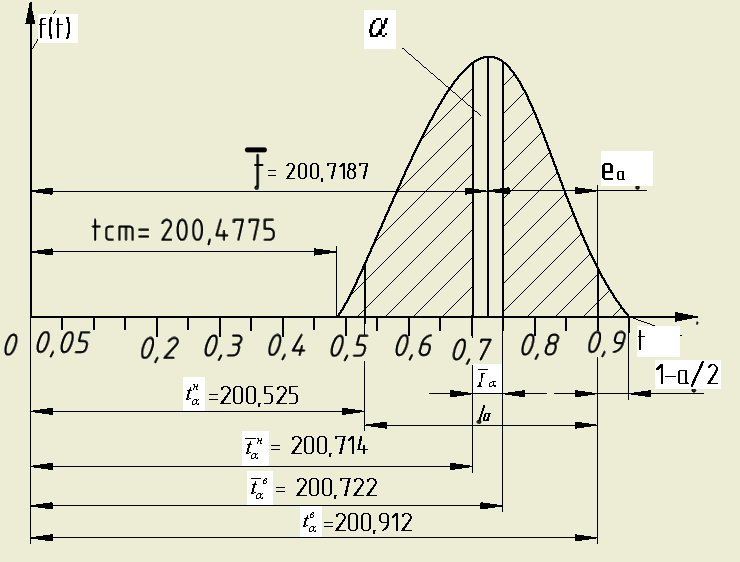
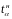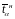Рисунок – 2 Взаимосвязь между доверительной вероятностью , возможной максимальной ошибкой е , доверительными границами рассеивания одиночного ( и ) и среднего и 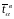значений ПН для ЗНР

Определим значения интегральной функции ЗНР в концах интервалов исходного статистического ряда, по таблице П.2. приложения, используя отношение .

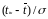Максимальную абсолютную ошибку для одиночного ПН определяют по формуле

е = =

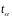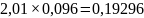
где - коэффициент Стьюдента, определяемый по значению доверительной вероятности и объему выборки N из таблицы П. 6 приложения.

Доверительные границы рассеивания при ЗНР рассчитывают соответственно по формулам

а) для нижней границы

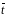= – е

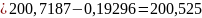
б) для верхней границы

= + е

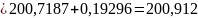
Интервал в который при заданной доверительной вероятности попадает 100 % от N показателей надежности, называют доверительным

интервалом I , и его определяют по формуле

I = –

Среднее квадратическое отклонение 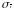при этом определяют по формуле

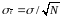
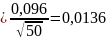
При законе нормального распределения и заданной доверительной вероятности показатели рассеивания среднего значения показателя надежности определяют по следующим формулам:

абсолютную ошибку по формуле

е =

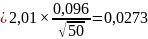
Доверительные границы рассеивания по формулам:

а) для нижней границы рассеивания

= – (е / )

б) для верхней границы рассеивания

= + (е / )

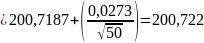
доверительный интервал 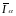по формуле

= -

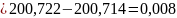
Относительную предельную ошибку переноса ( в процентах) независимо от ТЗР определяют по формуле

= 100( – ) / ( – )
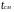