
var17 Юров
.docxЛипецкий государственный технический университет
Факультет инженеров транспорта
Кафедра транспортных средств и техносферной безопасности
Индивидуальное задание
по теории автоматических систем
Анализ характеристик линейной автоматической системы
Вариант 17
Студент _________
Группа ТК-18-1 подпись, дата
Руководитель ________ Юров М.Д.
ст. преподаватель подпись, дата
Липецк – 2021 г.
Использование аппарата дифференциальных уравнений обусловлено необходимостью количественной оценки действующих в системе сил и моментов и анализа качества САУ.
Дифференциальное уравнение динамики вида
 ;
;
Выполним линеаризацию исходного уравнения в окрестности координатных точек:
 =
4;
=
4;
 =
3;
=
3;
 =
3;
=
3;
 =
0,5.
=
0,5.
Большинство непрерывных САУ можно заменить (линеаризовать) эквивалентными системами, переходные процессы в которых описываются обыкновенными линейными дифференциальными уравнениями с постоянными коэффициентами.
Описание процессов САУ с помощью дифференциальных уравнений
Выбор метода линеаризации, то есть выбор приближения функции определяется конечной целью исследования. После линеаризации функций система переходит в систему линейных дифференциальных уравнений n-порядка.
Выполним линеаризацию исходного уравнения
;
1)
 ;
;
 ;
;
2)
 ;
;
 =0,02
=0,02 ;
;
3)
 ;
;
 ;
;
4)
 ;
;

Подставляя полученные значения
 .
.
Выполним переход к стандартной форме записи
 .
.
Окончательно имеем
13,25 .
.
Полученное уравнение динамики имеет силу для малых изменений координат и относится к классу линейных обыкновенных уравнений, анализ которых существенно проще.
Описание процессов через передаточные функции
Переход от дифференциального уравнения к однозначно соответствующему ему алгебраическому уравнению называют преобразованием Лапласа, комплексную переменную р – оператором Лапласа. Выполним преобразование Лапласа.
13,25
Отношение
 изображения выходной величины системы
к изображению его входной величины
называют передаточной функцией системы
в операторной форме.
изображения выходной величины системы
к изображению его входной величины
называют передаточной функцией системы
в операторной форме.
Соответственно отношение изображения выходной величины звена к изображению его входной величины называют передаточной функцией звена.
Передаточная функция в операторной форме

Частотные характеристики широко используются при анализе и синтезе САУ
Если на вход линейной разомкнутой системы или звена подать гармоническое возмущение, то по истечении некоторого времени, когда затухнут все движения, определяемые переходным процессом, на выходе звена или системы установится также гармоническое изменение выходной величины с той же частотой, которую имеет входная величина, но с иными амплитудой и фазой.
Амплитуда и фаза на выходе при прочих равных условиях будет зависеть от частоты возмущающего воздействия.
Передаточная функция в частотной форме

Модуль частотной передаточной функции

Аргумент передаточной функции

Выделим из передаточной функции вещественную и мнимые части




Вещественная часть

Мнимая часть




Построение характеристик
Построение графиков характеристик проводим в среде
ВЧХ – Вещественная частотная характеристика

Рисунок 1 – Исходные данные для построения графиков ВЧХ
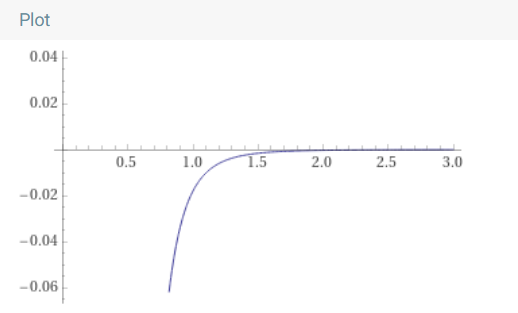
Рисунок 2 – Вещественная частотная характеристика, U(w), w ϵ (0…3)
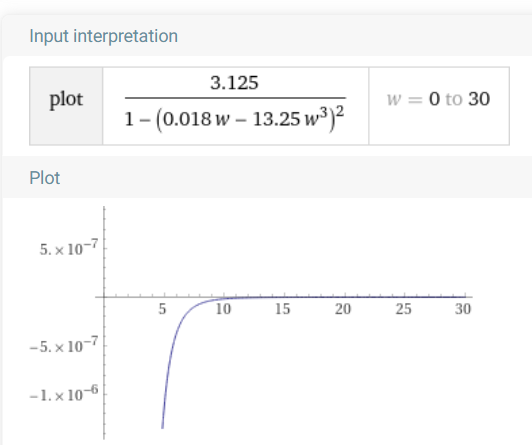
Рисунок 3 – Вещественная частотная характеристика, U(w), w ϵ (0…30)
АЧХ – Амплитудно-частотная характеристика
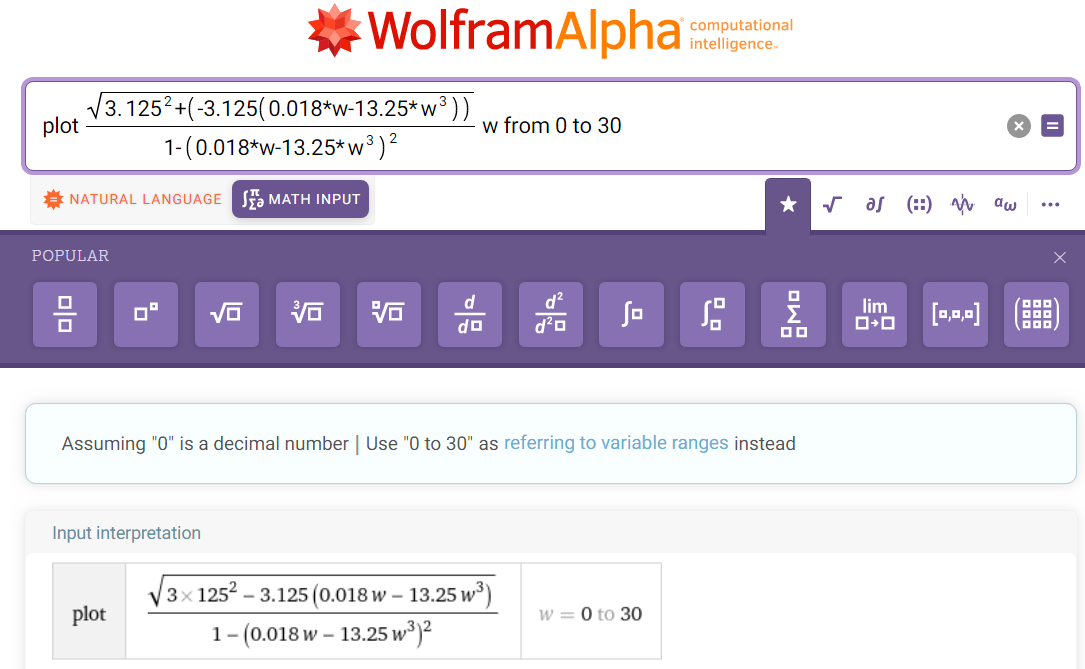
Рисунок 4 - Исходные данные для построения графиков АЧХ
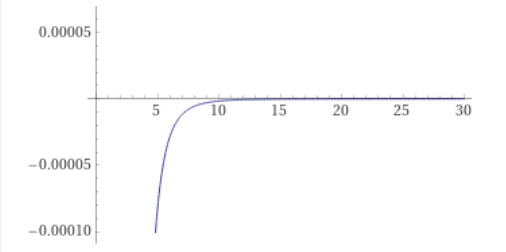
Рисунок 5 – Амплитудно-частотная характеристика, А(w), w ϵ (0…30)
ФЧХ – Фазо-частотная характеристика
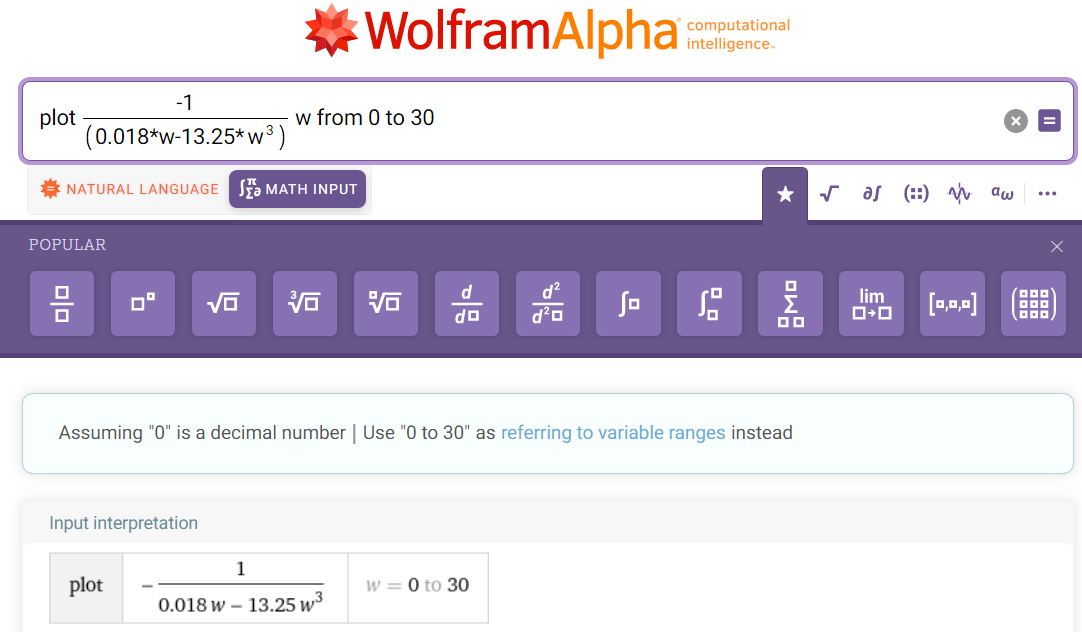
Рисунок 6 - Исходные данные для построения графиков ФЧХ
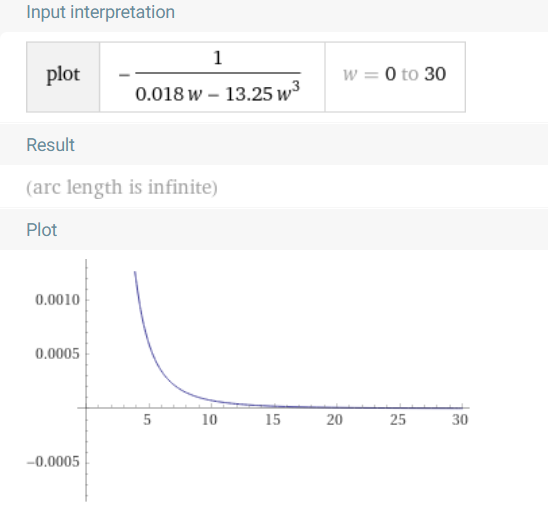
Рисунок 7 – Фазо-частотная характеристика, φ(w), w ϵ (0…30)
L(A)=20log( )
)

Рисунок 8 - Исходные данные для построения графиков ЛАЧХ

Рисунок 11 – ЛАЧХ, w ϵ (0,2…30)
L(φ)=20log(φ)
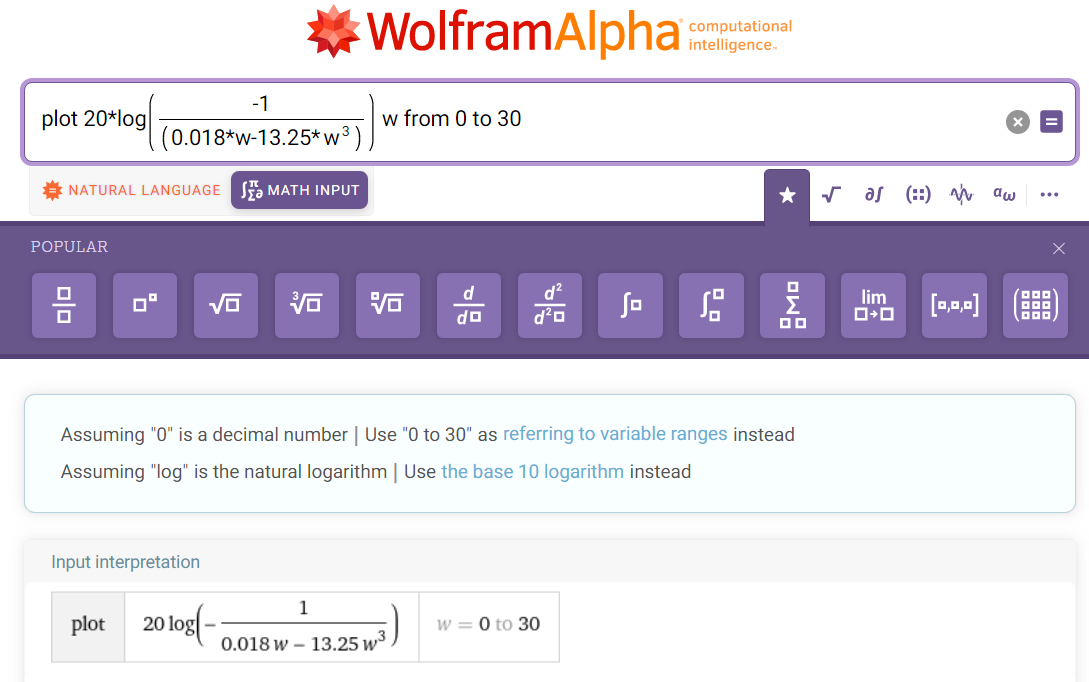
Рисунок 9 - Исходные данные для построения графиков ЛФЧХ

Рисунок 10 – ЛФЧХ, w ϵ (0,1…300)
АФЧХ – Амплитудная фазо-частотная характеристика


Рисунок 11 – Исходные данные для построения графиков АФЧХ
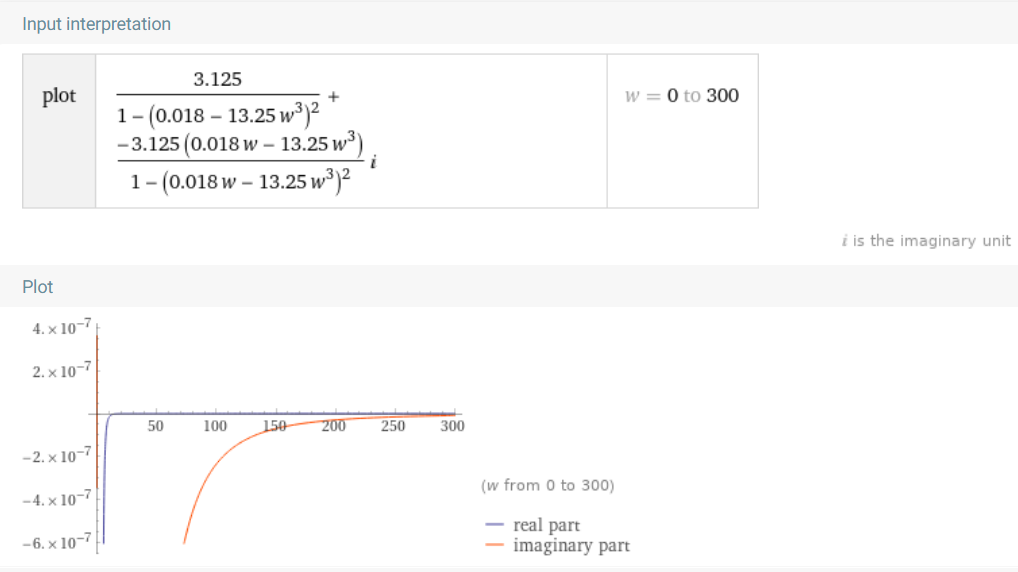
Рисунок 12 – АФЧХ (зависимость P(w) от Q(w))
Оценка устойчивости САУ
САУ, как любая динамическая система, характеризуется переходным процессом, возникающим в ней при нарушении ее равновесия под воздействием сигнала управления, настройки или помех.
Для того чтобы САУ могла правильно реагировать на сигнал управления, настройки или изменения нагрузки, в переходном процессе свободная составляющая с течением времени должна стремиться к нулю, так как характер свободного движения системы определяет ее устойчивость.
Критерий Ляпунова
Среди корней характеристического уравнения отсутствуют нулевые и чисто мнимые корни; вещественные части всех корней характеристического уравнения отрицательные.
13,25
Отношение изображения выходной величины системы к изображению его входной величины называют передаточной функцией системы в операторной форме.
Соответственно отношение изображения выходной величины звена к изображению его входной величины называют передаточной функцией звена.
Передаточная функция в операторной форме
Характеристическое уравнение
 .
.
Корни уравнения
 .
.
Вывод:
Только один корень имеет отрицательную вещественную часть, следовательно, САУ неустойчива.
Годограф Михайлова
Характеристическое уравнение
 .
.
Получаем характерный вектор
 .
.
Выделим вещественную и мнимую части
 .
.
Вещественная часть
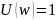 .
.
Мнимая часть
 .
.
Задаваясь
значением
 (0; 0,1; 0,2; и т.д.) вычисляем отдельно
вещественную часть
(0; 0,1; 0,2; и т.д.) вычисляем отдельно
вещественную часть
 и мнимую
и мнимую
 часть характеристического вектора.
часть характеристического вектора.
С их помощью строим годограф Михайлова
Рисунок 13 – Исходные данные для построения годографа Михайлова

Рисунок 14 – Годограф Михайлова
Для устойчивой системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности повернулся против часовой стрелки, начиная с вещественной оси, на число квадрантов равное порядку характеристического уравнения, последовательно проходя эти квадранты.
Условие устойчивости не выполняется.
Оценка качества САУ
Для решения дифференциального уравнения воспользуемся методом Рунге-Кутта: solve {13.25y'''+0.018y'+1=3.125, y(0)=0, y'(0)=0, y'''(0)=0} r k f method from 0 to 100.
Имеем следующий график переходного процесса:

Рисунок 15(а) – Расчёт уравнения в Wolfram Alpha методом Рунге-Кутта
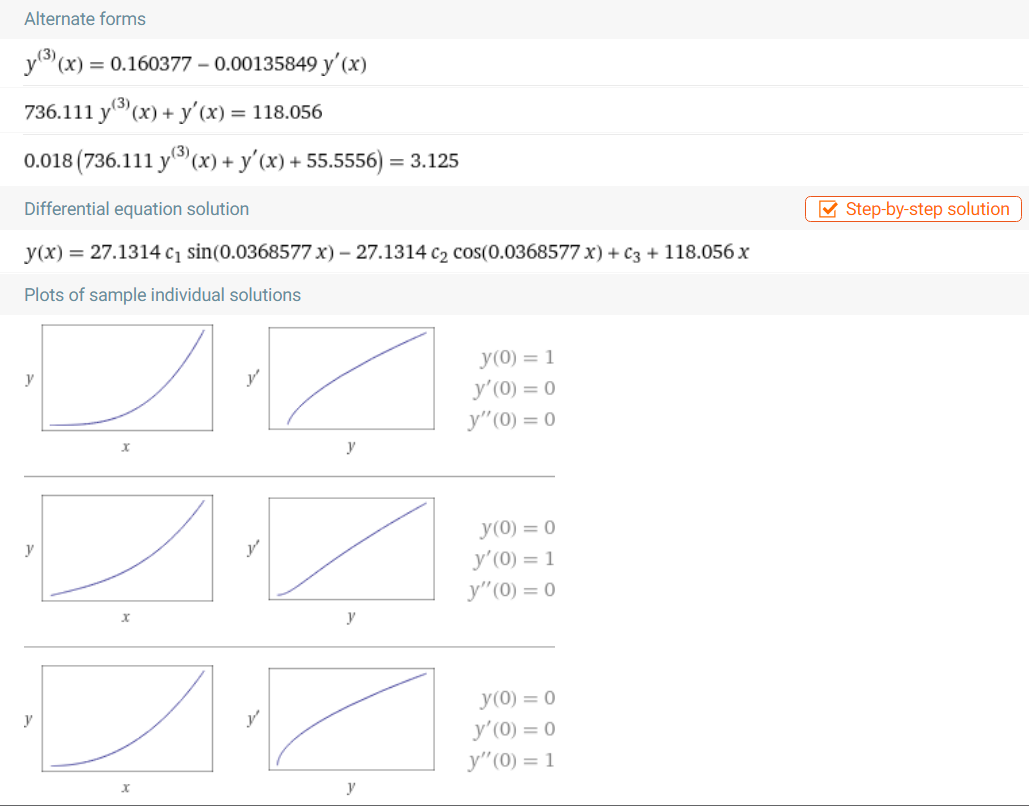 Рисунок
15 (б) – Расчёт уравнения в Wolfram Alpha методом
Рунге-Кутта
Рисунок
15 (б) – Расчёт уравнения в Wolfram Alpha методом
Рунге-Кутта
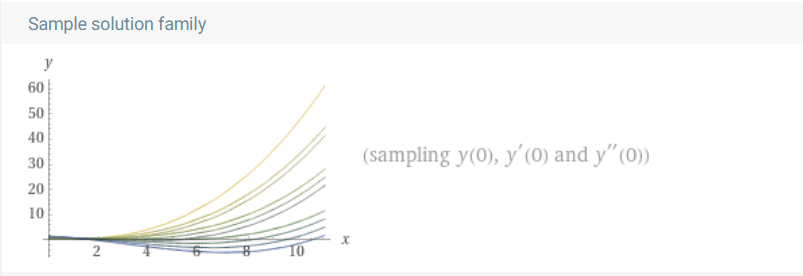
Рисунок 15 (в) – Расчёт уравнения в Wolfram Alpha методом Рунге-Кутта
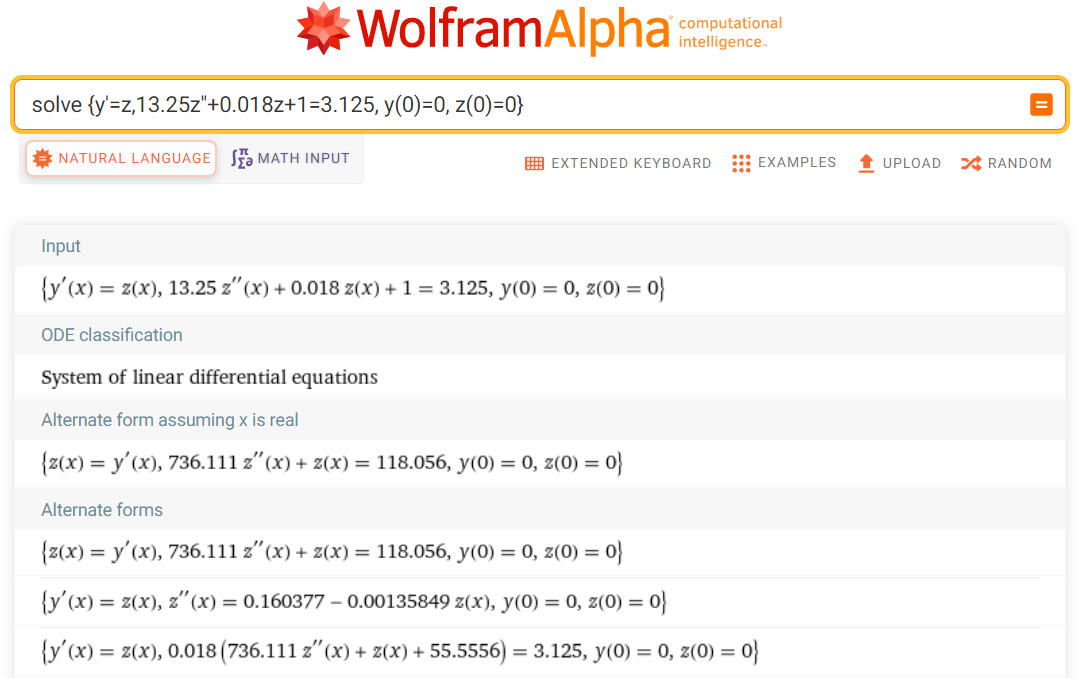
 Рисунок
16 – Решение исходного линеаризованного
дифференциального уравнения третьего
порядка при единичном возмущении (x = 1)
в среде Wolfram Alpha
Рисунок
16 – Решение исходного линеаризованного
дифференциального уравнения третьего
порядка при единичном возмущении (x = 1)
в среде Wolfram Alpha
САУ неустойчива, так как при исследовании подтвердились выводы о ее неудовлетворительных свойствах.
Вывод:
В процессе выполнения индивидуального задания по нелинейному дифференциальному уравнению было проведено исследование свойств САУ. На начальном этапе проведена линеаризация исходного нелинейного ДУ и приведение его к стандартной формы записи; проведено исследование графиков в среде MathCAD вещественной частотной (ВЧХ), амплитудно-частотной (АЧХ), фазо-частотной (ФЧХ), логарифмической амплитудно-частотной (ЛАЧХ), логарифмической фазо-частотной (ЛФЧХ) и амплитудной фазо-частотной характеристик (АФЧХ). Была проведена оценка устойчивости САУ по алгебраическому критерию Ляпунова и частотному критерию Михайлова. САУ оказалась не устойчивой. Далее проведена оценка качества САУ с использованием среды Wolfram Alpha. Итогом анализа САУ стало заключение о том, что она является неустойчивой.
