Пособие надежность. Ч1

ложения основных поверхностей. Определение спектров амплитуд и фаз гармонических составляющих отклонений формы и расположения основных поверхностей деталей машин необходимо для выявления доминирующих гармоник с целью эксплуатационно-конструкторского обоснования норм точности и разработки технологических мероприятий по их уменьшению. Поэтому качественная и количественная оценки спектров амплитуд и фаз отклонений формы и взаимного расположения высокоточных поверхностей деталей машин представляет практический интерес.

В общем случае отклонения формы и радиальное биение поверхностей вращения могут быть представлены тригонометрическим полиномом Фурье р- ого порядка

k =1

где Ak и γk – соответственно амплитуда и начальная фаза k- ой гармонической составляющей отклонений текущего радиуса-вектора ∆R(φi) рассматриваемого профиля поперечного сечения поверхности относительно общей оси вращения детали; р – порядок полинома, т. е. число его членов; φi – текущий угол, т. е. угол поворота радиуса-вектора относительно выбранного начала отсчета.

Члены тригонометрического полинома (2.11) представляют влияние на текущую величину отклонений радиуса-вектора ∆R(φi) элементарных погрешностей обработки: первый – эксцентриситета профиля относительно общей оси вращения; второй – эллипсности; третий – огранки с трехвершинным профилем и т. д.

Согласно отечественным стандартам нормирование отклонений формы по некруглости производится как максимальное отклонение реального профиля от вписанной или описанной относительно круглограммы окружности, положение которой определяется тремя и более точками реального профиля случайного характера. Некруглость определяется в интересуемой плоскости поперечного сечения детали. Формирование нецилиндричности намного более

90

сложное явление, которое комбинирует данные от множественных профилей некруглости поперечных сечений в единую реальную форму поверхности вращения. Нормирование нецилиндричности по отечественным стандартам осуществляется как наибольшее отклонение реальной поверхности вращения от вписанного или описанного цилиндра относительно этой поверхности.

Использование прилегающих окружностей и цилиндров для поверхностей вращения в качестве баз отсчета вызвано тем, что они соответствуют условиям сопряжения и функционирования при посадках с нулевыми зазорами. Однако на базе прилегающих линий и поверхностей во многих случаях невозможно получить однозначный результат измерений для валов и отверстий даже в близлежащих сечениях. Например, некруглость и нецилиндричность в близлежащих сечениях оцениваются значениями, отличающимися друг от друга на

10…15 % и более.

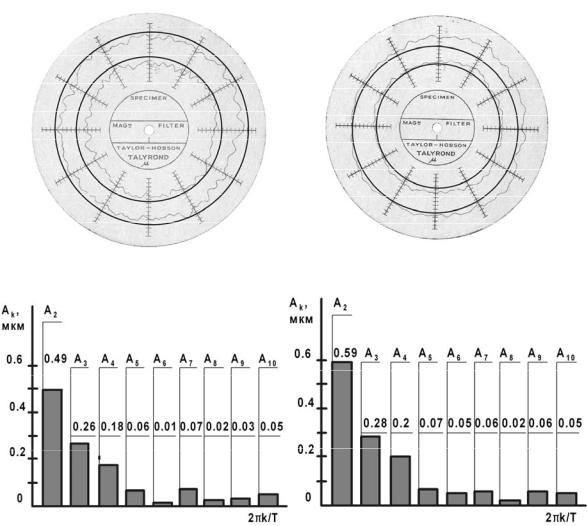
На рис. 2.27 представлены круглограммы и усредненные линейчатые спектры амплитуд опорной шейки вала после обычного чистового шлифования и втулки подшипника скольжения после тонкого растачивания резцом из сверхтвёрдого материала (Эльбор-Р) с расположением описанных и вписанных окружностей при оценке некруглости в близлежащих сечениях на расстоянии 10…15 мм.

Даже при визуальной оценке неровностей профилей в близлежащих сечениях на круглограммах видна нестабильность отклонений формы и волнистости по величине и фазе.

В английском стандарте на методы определения отклонений от круглости за базу отсчета применяется средняя окружность, проведенная по принципу наименьших квадратов. Современные кругломеры типа «TALYROND» (модификаций 73-Р, 440, 450) английской фирмы «TAILOR-HOBSON»

оснащены программным обеспечением для гармонического анализа отклонений от правильной формы и концентричности исследуемых профилей поверхностей деталей машин, в том числе коленчатых и распределительных валов, блоков цилиндров и др.

91

х2500 А х2500 А

Рис. 2.27. Круглограммы и усредненные линейчатые спектры амплитуд соответственно а – опорной шейки вала и б – втулки подшипника скольжения

Врезультате записи множества реализаций некруглости профилей поверхности вращения в фиксированных по осевой координате поперечных сечениях выявляются также амплитуды неконцентричности их геометрических центров в общем спектре гармонических составляющих результирующих отклонений.

Впринятом представлении комплексным параметром оценки отклонений текущего радиуса-вектора ∆R(φi) по некруглости и неконцентричности геометрического центра контролируемого профиля является радиальное биение.

92

Так как гармонические составляющие различных частот не коррелированны между собой, дисперсия радиального биения контролируемого профиля, вызываемого ими, равна

Это позволяет определить «удельный вес» каждой гармонической составляющей в результирующих отклонениях исследуемого профиля.

В производственной практике контроль радиального биения осуществляется либо с установкой в центрах, либо с установкой на призмах, а крупногабаритных валов – на двухопорных люнетах.

Способ контроля радиального биения поверхности с установкой детали в центрах нельзя признать методически обоснованным, так как он не отвечает требованиям функциональной взаимозаменяемости сопрягаемых поверхностей в работающей сборочной единице.

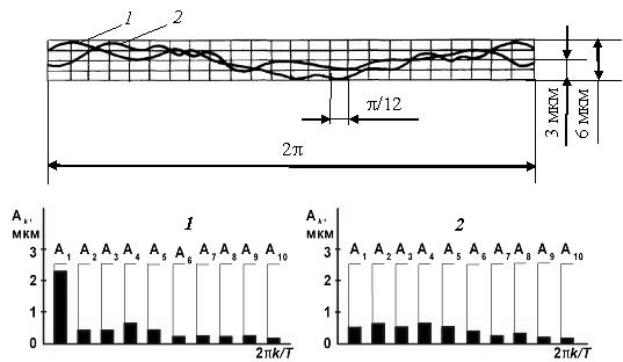
Метод контроля радиального биения поверхностей деталей с установкой на призмах также является косвенным, но имеет более определенный характер. При непрерывной записи показаний измерительного датчика радиальное биение контролируемого профиля поверхности имеет вид периодической кривой с периодом 2π, которая в результате разложения в тригонометрический ряд Фурье может быть представлена в виде спектров амплитуд и начальных фаз гармонических составляющих. На рис. 2.28 представлены осциллограммы и линейчатые спектры амплитуд радиального биения левой и правой опорных шеек вала под подшипники качения.

Представляет интерес дать оценку погрешностям измерения при производственном методе контроля радиального биения поверхностей деталей машин с установкой на призмах.

Известно, что при контроле радиального биения с установкой детали на призмах (люнетах) результаты измерения зависят от спектров амплитуд и фаз отклонений базовых поверхностей и углов расположения опорных граней

93

призм или опорных элементов люнетов и точки контакта измерительного датчика ψ и α. Наиболее часто применяются схемы измерения радиального биения с помощью призм с углами 90°, 120° и 60° при вертикальном или горизонтальном расположении измерительного датчика.

Рис. 2.28. Осциллограммы и линейчатые спектры амплитуд радиального биения левой и правой опорных шеек вала под подшипники качения

Проведенные исследования показали, что при установке деталей на призмах или двухопорных люнетах отдельные гармонические составляющие спектров отклонений формы базовых поверхностей в зависимости от углов ψ и α расположения опорных элементов и точки контакта измерительного датчика оказывают различное влияние на погрешность базирования и результаты измерения.

Влияние каждой гармонической составляющей отклонений формы базовой поверхности на погрешность измерения при конкретных схемах производственного контроля радиального биения характеризуется коэффициентом воспроизведения, представляющим собой отношение

94

где А'kб – амплитуда k-ой гармонической составляющей отклонений, полученных в результате измерения текущих положений точек контролируемого профиля опорного сечения базовой поверхности при вращении детали; Аk – амплитуда соответствующей k-ой гармонической составляющей собственных отклонений формы реального профиля опорного сечения базовой поверхности.

Значения коэффициентов воспроизведения гармонических составляющих для конкретных схем контроля могут быть определены по формуле

где Кk и εk – соответственно функция передаточных коэффициентов и составляющая углов сдвига фаз изменения k-ых гармоник, обусловленные влиянием углов расположения опорных граней призм или опорных элементов люнетов и точки контакта измерительного датчика.

Значения функции передаточных коэффициентов Кk и составляющей εk углов сдвига фаз изменения k-ых гармоник при конкретных схемах контроля радиального биения поверхностей деталей с установкой на призмах или двухопорных люнетах определяется по формулам

Теоретические значения функции передаточных коэффициентов Kk и коэффициентов воспроизведения Sk гармонических составляющих k=2…10 в направлениях вертикальной и горизонтальной координатных осей для наиболее применяемых схем измерения при использовании призм с углами

ψ=90°, ψ=120° и ψ=60° приведены в табл. 2.4.

95

Таблица 2.4 Теоретические значения функции передаточных коэффициентов Kk и коэффициентов воспроизведения Sk гармонических составляющих k=2…10

В результате исследования спектров отклонений формы поверхностей трения валов и втулок подшипников скольжения установлено, что макрогеометрические отклонения от круглости и цилиндричности, с некоторыми допущениями, можно аппроксимировать суммой гармоник 2-ого, 3-его и 4-ого порядков. На их долю приходится до 70…80 % дисперсии результирующих отклонений формы. Анализ величин и углового расположения гармонических составляющих некруглости левой и правой опорных шеек валов и сопрягаемых с ними втулок подшипников скольжения по результатам проведенных статистических исследований показал, что одноименные гармоники в их спектрах имеют амплитуды неодинаковой величины, которые по фазе не совпадают и носят случайный характер. Относительное распределение амплитуд гармоник 2-ого, 3-его и 4-ого порядков А2:А3:А4 в спектрах макрогеометрических отклонений формы основных поверхностей деталей различного назначения соответствуют диапазону от 1,0:0,5:0,4 до 1,0:0,4:0,2. При оценке неровностей реальных

96

профилей в близлежащих сечениях на расстоянии 10…15 мм на круглограммах отмечается большая нестабильность макрогеометрических отклонений и волнистости по величине и фазе. Следовательно, положение прилегающих цилиндров при оценке цилиндричности этих поверхностей также носит случайный характер. Этим объясняется разница оценочных показателей некруглости и нецилиндричности поверхностей вращения деталей машин и неравномерный износ поверхностей трения скольжения.

6. Исследование погрешности базирования заготовок типа тел вращения при установке на призмах или двухопорных люнетах

В производственной практике при измерении или обработке деталей типа тел вращения широко применяют схемы установки на призмах или двухопорных люнетах (контроль радиального биения, отклонений формы, зацентровка валов, растачивание отверстий, шлифование валов, гильз, колец, фрезерование пазов, лысок, и т. п.). При выполнении этих операций схема базирования, характеризуется углами ψ и α (рис. 2.29) расположения опорных элементов люнетов (граней призм) и точки (линии) контакта измерительного или режущего инструмента с контролируемой или обрабатываемой поверхностью. При этом, вследствие отклонений формы базовых поверхностей, возникает составляющая (∆εбф) суммарной погрешности базирования (∆εб), которая в зависимости от углов ψ и α расположения опорных элементов и точки контакта инструмента может быть соизмерима и даже превосходить отклонения формы базовых поверхностей.

Как уже отмечалось, отклонения ∆R(φi) текущего радиуса-вектора R(φi) профиля поперечного сечения реальной поверхности вращения детали могут быть представлены тригонометрическим полиномом Фурье р-ого порядка

(2.11).

Очевидно, что переменные по углу поворота ошибки радиусов-векторов опорных профилей базовых поверхностей будут предопределять различные величины смещения оси заготовки при изменении ее углового положения. Ес-

97

ли за измерительную базу принята общая ось базовых поверхностей, то составляющая погрешности базирования ∆εбф, обусловленная макрогеометрией профилей опорных сечений, определяется величиной смещения оси в направлении выдерживаемого при обработке или измеряемого при контроле размера. Если же за измерительную базу принята образующая поверхности вращения, то погрешность базирования ∆εбф определяется как сумма текущей ошибки радиуса-вектора измерительной базы ∆R(φi) и величины смещения оси ∆u2,р(φi,yм) в рассматриваемом поперечном сечении в направлении выдерживаемого при обработке или измеряемого при контроле размера, т. е.

При установке заготовки на призмах или двухопорных люнетах отдельные гармонические составляющие спектров отклонений формы базовых поверхностей в зависимости от углов ψ и α расположения опорных элементов и точки контакта инструмента оказывают различное влияние на погрешность базирования. Путем подбора углов расположения опорных элементов люнетов или призм и точки контакта инструмента можно исключить влияние доминирующих гармонических составляющих спектров отклонений формы базовых поверхностей на составляющую ∆εбф и тем самым уменьшить общую погрешность базирования. Влияние каждой гармонической составляющей отклонений формы базовых поверхностей на погрешность базирования при конкретных схемах установки определяется функцией передаточных коэффициентов

(2.15).

В случае, когда измерительной базой является образующая цилиндрической поверхности вращения это влияние можно характеризовать коэффициентом воспроизведения (2.13).

Теоретические значения коэффициентов Kk и Sk гармонических составляющих в направлениях вертикальной и горизонтальной координатных осей для наиболее применяемых схем измерения приведены в табл. 2.4.

98

Для конкретного профиля поперечного сечения заготовки составляющая погрешности базирования ∆εбф, обусловленная смещением оси вследствие отклонений формы базовых поверхностей, определяется по формуле:

где yм – продольная координата от среднего опорного сечения левой базовой шейки до интересуемого; L – расстояние, между средними опорными поперечными сечениями левой и правой базовых поверхностей; Akл, Akп, γkл, γkп – соответственно амплитуды и начальные фазы k-ых гармонических составляющих реальных отклонений формы профилей средних опорных сечений левой и правой базовых поверхностей; εk – составляющая углов сдвига фаз изменения k- ых гармоник, обусловленная параметрами ψ и α.

Значения функции коэффициентов воспроизведения Sk, функции передаточных коэффициентов Kk и составляющей углов сдвига фаз изменения εk k-ых гармоник определяются по формулам (2.14), (2.15) и (2.16) соответственно.

Таким образом, для определения составляющей ∆εбф суммарной погрешности базирования ∆εб необходимо иметь данные о спектрах амплитуд и начальных фаз фактических отклонений формы реальных профилей опорных сечений базовых поверхностей.

Исследование выполнялось на специальных образцах типов «А» и «Б» (рис. 2.30) и установочном приспособлении (рис. 2.29), состоящем из плиты 1, смонтированных на ней центровых бабок 5, 9, двухопорных люнетов 2, 4 с поворотными вкладышами 11 и индикаторной стойки 3. На люнетных и индикаторной стойках закрепляются индикаторы 7 (цена деления 0,001 мм) для измерения радиального биения шеек образцов в вертикальной и горизонтальной плоскостях. В центровых бабках установлены выдвижные срезанные центры 6, 8 с плоскими упорными поверхностями, один из которых (поз. 6) подпружинен. Выдвижные центры фиксируют образцы валов в осевом направлении через шарики, закладываемые в центровые отверстия образцов после их уста-

99