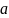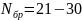цос 2сем / Obrazets_otcheta_LR17 (2)

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Федеральное государственное образовательное бюджетное учреждение

высшего образования

«Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М. А. Бонч-Бруевича»

_____________________________________________________________________________

Кафедра радиотехники

Дисциплина «Цифровая обработка сигналов»

Лабораторная работа № 17

СПЕКТРАЛЬНЫЙ АНАЛИЗ: ПАРАМЕТРИЧЕСКИЕ МЕТОДЫ

Выполнили: ст. гр. РТ-2x

№_бр 13

Проверил: ассистент каф. РТ,

Бойко И.А. ______

Санкт-Петербург

2024

СОДЕРЖАНИЕ ОТЧЕТА

ТАБЛИЦА ИСХОДНЫХ ДАННЫХ

Переменная	Назначение	Значение			Идентификатор
	Номер бригады				Nb = 13
	Длина воздействия				L = 2048
	Частота дискретизации				Fs =8000
	Заданные (истинные) параметры АР-модели
		1	1	1		Вектор a = [1 -0.1 0.2 0.2 0.1 0.3]
		-0.86	-0.1	0.5
		0.54	0.2	0.17
		-0.3	0.2	0.3
		-0.17	0.1	0.1
		0.22	0.3	0.1
		-0.1	—	-0.1
		—	—	-0.5

Формула СПМ:

• смысл всех переменных:

N-длина случайного эргодического процесса;

T=1/fд – период последовательности (случайного эргодического процесса);

F д – частота дискретизации;

- спектральная плотность последовательности x(n);

Множитель 1/fд=T учитывает связь между СПМ дискретного и аналогового сигналов, подобно связи между спектральными плотностями данных сигналов.

• Свойства СПМ:

СПМ S( ) – неотрицательная, четная, периодическая функция частоты с периодом, равным 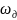=2пfд=2п/T, и эти свойства сохраняются для её оценки ;

При конечной длине N эргодического процесса x(n) говорят об оценке СПМ , которая даёт картину распределения средней мощности по частоте и измеряется в ваттах на герц (Вт/Гц) или децибелах на герц (дБ/Гц)

Теорема Винера-Хинчина (формула):

• смысл всех переменных:

- спектральная плотность мощности;

T- период;

- корреляционная функция;

m- отсчёты корреляционной функции

Суть параметрических методов состоит в построении математической модели анализируемой последовательности (эргодического случайного процесса) и оценке параметров модели, при которых обеспечивается наилучшее приближение моделируемой последовательности к анализируемой по заданному критерию.

Этапы расчёта оценки СПМ:

1) Выбор модели (АР, СС, АРСС)

2) Оценка порядка модели

3) Оценка параметров модели

4) Расчёт оценки СПМ

АР-модели соответствует БИХ-фильтр полюсного вида (чисто рекурсивный) с передаточной функцией при b0=1:

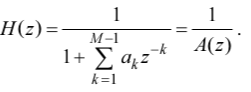
РУ АР-модели:

Где – параметры АР-модели, (M-1) – порядок АР-модели, e(n) – белый гауссовский шум

Рис.1. Структурная схема АР-модели.

СС-модели соответствует КИХ-фильтр с передаточной функцией:

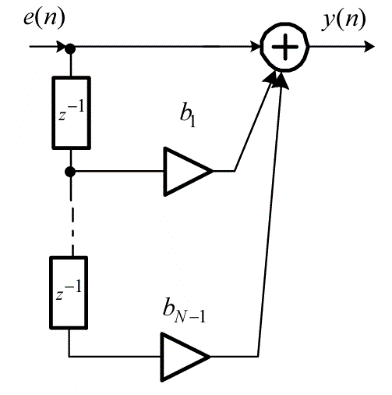
РУ СС-модели:

– параметры СС-модели, (N-1) – порядок СС-модели

Рис.2. Структурная схема СС-модели.

А 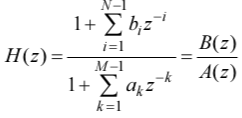РСС-модели соответствует БИХ-фильтр с дробно-рациональной передаточной функцией:

Рис.3. Структурная схема АРСС-модели.

РУ АРСС-модели:

и - параметры АРСС-модели, (M-1) – порядок АРСС-модели при (N-1) (M-1).

п.1. Моделирование случайной последовательности на основе АР-модели

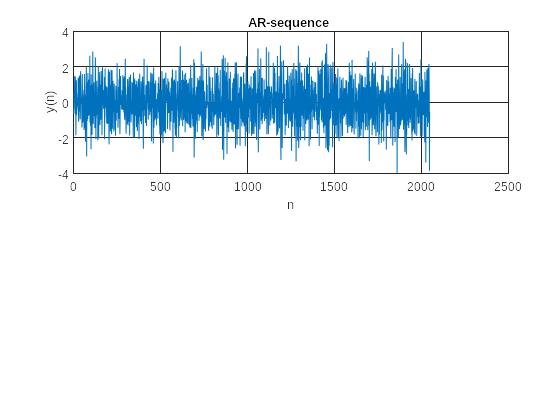
Рис. 1 График моделируемой последовательности

Пояснения:

С какой целью используют АР-модель;

• АР-модель считается наиболее подходящей для оценки СПМ с острыми пиками, но без глубоких впадин;

Чему равен порядок АР-модели;

• Порядок АР-модели равен M-1;

Какие элементы вектора a относят к параметрам АР-модели.

• - параметры АР-модели (кроме ).

п.2. Вычисление истинной СПМ моделируемой последовательности

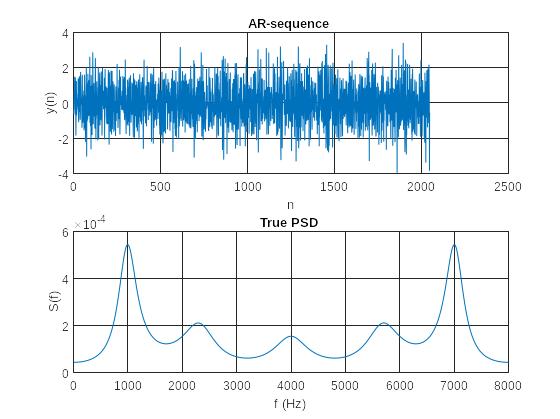
Рис. 2 График истинной СПМ моделируемой последовательности

Пояснения:

Чему равен период СПМ;

• Период истинной СПМ равен 1/fд;

В каком случае достаточно вычислить СПМ в основной полосе частот

• Достаточно вычислить СПМ в основной полосе частот, когда сигнал периодический, когда нужно оценить энергию сигнала (большая часть энергии в основной полосе частот);

Вид СПМ (наличие пиков и впадин) в основной полосе частот.

• Видим гладкую картину СПМ, что соответствует АР-модели. Есть несколько выраженных пиков (максимальная мощность сигнала), впадины.

п.3. Оценка оптимального порядка АР-модели анализируемой последовательности

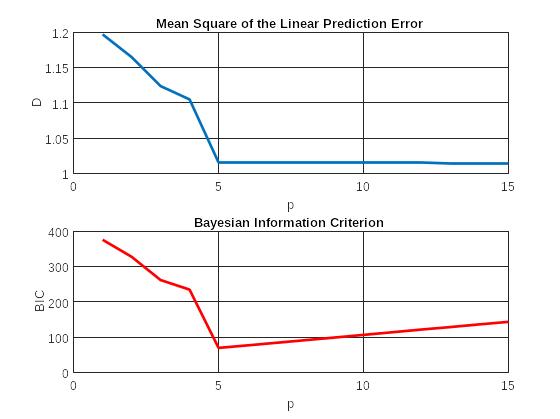
Рис. 3 Графики зависимостей среднего квадрата ошибки линейного предсказания и значений критерия Байеса от порядка модели

Оптимальный порядок АР-модели: p_opt = 5

Пояснения:

Какая последовательность выбрана в качестве анализируемой;

• В качестве анализируемой последовательности выбрана модулированная последовательность y(n);

Как определяется оптимальный порядок АР-модели по графику;

• Поиск порядка p, при котором достигается минимум функции:

Информационный критерий Байеса:

Зависимость среднего квадрата ошибки линейного предсказания от порядка модели.

• При увеличении порядка АР-модели средний квадрат ошибки линейного предсказания стремится к 1.

п.4. Вычисление оценок параметров АР-модели

Истинных параметров АР-модели и их оценок

ИСТИННЫЕ ПАРАМЕТРЫ a = [1 -0.1 0.2 0.2 0.1 0.3]

МЕТОД ЮЛА-УОЛКЕРА aYW = [1 -0.081244 0.19676 0.21163 0.096176 0.28455]

МЕТОД БЕРГА aBURG = [1 -0.080818 0.19737 0.2124 0.096483 0.28532]

КОВАРИАЦИОННЫЙ МЕТОД aCOV = [1 -0.080653 0.19703 0.21259 0.09686 0.2863]

МОДИФИЦИРОВАННЫЙ КОВАРИАЦИОННЫЙ МЕТОД

aMCOV = [1 -0.080582 0.19663 0.2112 0.096629 0.28533]

Средний квадрат ошибок линейного предсказания

МЕТОД ЮЛА-УОЛКЕРА: DYW = 1.0156

МЕТОД БЕРГА: DBURG = 1.0146

КОВАРИАЦИОННЫЙ МЕТОД: DCOV = 1.0167

МОДИФИЦИРОВАННЫЙ КОВАРИАЦИОННЫЙ МЕТОД: DMCOV = 1.0133

ОЦЕНКА ДИСПЕРСИИ НОРМАЛЬНОГО БЕЛОГО ШУМА: D = 1.016

Пояснить:

Что такое оценки параметров АР-модели;

Метод Юла-Уолкера (автокорреляционный). В этом методе оценивание параметров АР-модели производится по отсчетам анализируемой последовательности длины L, а моделируемая последовательность y(n) рассматривается как линейное предсказание вперед x ̂(n) анализируемой последовательности x(n) — линейная комбинация ее предшествующих отсчетов:

Метод Берга (Burg method) основан на вычислении оценок параметров АР-модели непосредственно по отсчетам последовательности (без вычисления оценки АКФ) с линейным предсказанием вперед (forward) и назад (backward) с минимизацией усредненной суммы средних квадратов ошибок линейного предсказания.

Ковариационный метод основан на вычислении оценки АКФ по известным отсчетам последовательности x(n) (без добавления нулей в начале и в конце), для чего последняя усекается симметрично справа и слева на (M-1) отсчётов, и оценка АКФ нормируется к длине усеченной последовательности [L-2(M-1)]. В соответствующей СЛАУ корреляционная матрица не является матрицей Тёплица.

Какие выводы следуют по результатам сравнения;

Модифицированный ковариационный метод основан на вычислении оценки АКФ для расширенной последовательности, составленной из последовательностей с линейным предсказанием вперед и назад. Оценка АКФ вычисляется так же, как в ковариационном методе, и нормируется к удвоенной длине последовательности 2[L-2(M-1)]. В соответствующей СЛАУ корреляционная матрица не является матрицей Теплица.

С чем сравниваются полученные оценки параметров;

Сравнивают анализируемую последовательность с моделируемой

Какие выводы следуют по результатам сравнения;

Если ошибка линейного предсказания ε(n) представляет собой нормальный белый шум e(n) , параметры линейного предсказания k a будут совпадать с параметрами АР-модели. В действительности, однако, ошибка ε(n) не обязательно является нормальным белым шумом, поэтому, вычислив параметры линейного предсказания a_k , можно получить оценки параметров АР-модели ˆak , которые обеспечат наилучшее приближение моделируемой последовательности к анализируемой по заданному критерию.

Какова связь между средним квадратом ошибки линейного предсказания и дисперсией нормального белого шума.

п.5. Проверка устойчивости БИХ-фильтра

Рис. 4 Карт нулей и полюсов

Пояснения:

Являются ли БИХ-фильтры устойчивыми;

БИХ-фильтры не всегда устойчивы;

По какому критерию проверяется устойчивость;

Если полюсы передаточной функции лежат внутри единичной окружности в z-плоскости, то БИХ-фильтр устойчивый;

Какие методы гарантируют устойчивость БИХ-фильтра

Устойчивость БИХ-фильтра гарантируется методом Юла-Уолкера и Берга.

п.6. Вычисление оценок СПМ

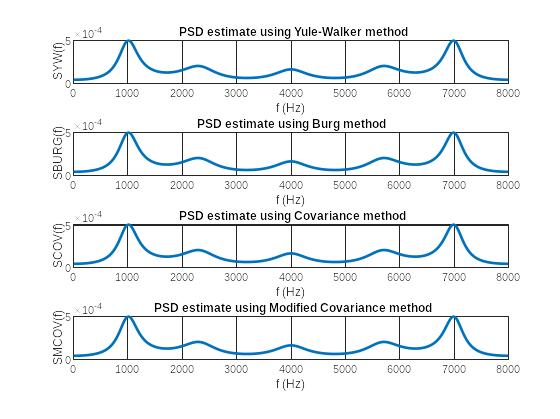
Рис. 5 Графики оценок СПМ

Сделать вывод о наличии пиков и впадин по графикам оценок СПМ в основной полосе частот: Выраженные пики, впадины между пиками. Графики практически совпадают друг с другом.

п.7. Сравнение оценок СПМ c истинной СПМ

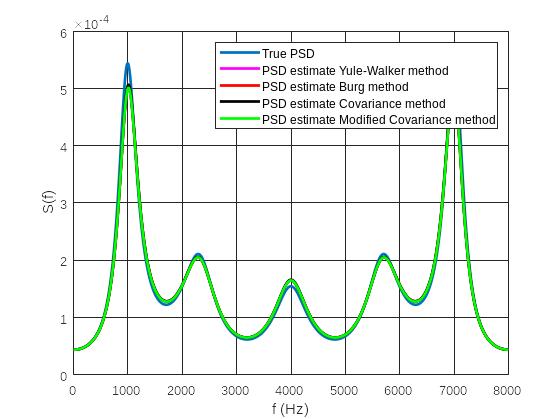
Рис. 6 График оценок СПМ и истинной СПМ

Пояснить результаты сравнения оценок СПМ с истинной СПМ (появление ложных пиков и впадин, смещение пиков и впадин, изменение значений СПМ, соответствующих частотам пиков и впадин): сравнивая графики оценок СПМ и истинной СПМ, можно сделать вывод, что присутствует смещение пиков и впадин, также присутствует изменения значений СПМ, соответствующих частотам пиков и впадин.

п.8. Вычисление значений RMSE

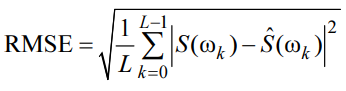
Значения RMSE оценок СПМ:

МЕТОД ЮЛА-УОЛКЕРА: RMSE_YW = 1.1526e-05

МЕТОД БЕРГА: RMSE_BURG = 1.1415e-05

КОВАРИАЦИОННЫЙ МЕТОД: RMSE_COV = 1.0792e-05

МОДИФИЦИРОВАННЫЙ КОВАРИАЦИОННЫЙ МЕТОД: RMSE_MCOV = 1.1507e-05

Пояснить результаты сравнения оценок СПМ (близость к истинной СПМ):

Используется на этапе моделирования для сравнительного анализа оценок СПМ (истинная СПМ для модулированной последовательности при ak -> анализируемая=модулированная -> оценки параметров модели -> оценка СПМ). Чем меньше RMSE, тем лучше используется оценка СПМ.

Оценка СПМ методом Берга самая близкая к истинному значению.

п.9. Исследование влияния порядка АР-модели на оценку СПМ

Рис. 7 График истинной СПМ и оценок СПМ по методу Юла-Уолкера

Пояснить, к каким изменениям в оценке СПМ по методу Юла—Уолкера при водит занижение и завышение порядка АР-модели относительно его оптимального значения (сглаживание оценок СПМ, расщепление пиков, смещение пиков и впадин, изменение значений СПМ, соответствующих частотам пиков и впадин).

При занижении порядка мы наблюдаем смещение пиков и впадин, а также изменение значений СПМ; при завышении порядка мы наблюдаем помимо смещения пиков и впадин, и изменений значений СПМ появление ложных пиков, ложных впадин.

п.10. Исследование влияния длины последовательности на оценку СПМ

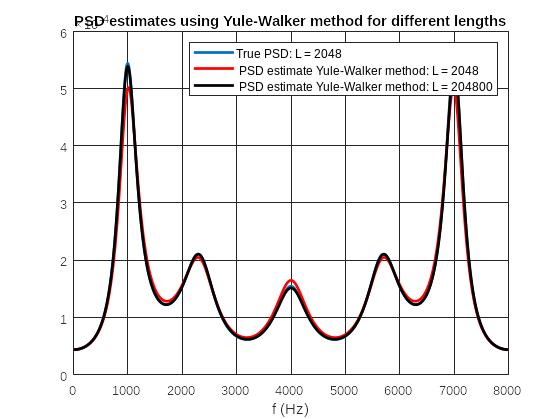
Рис. 8 График истинной СПМ и оценок СПМ по методу Юла-Уолкера

Пояснить, к каким изменениям в оценке СПМ по методу Юла—Уолкера при водит существенное возрастание длины последовательности (смещение пиков, изменение значений СПМ, соответствующих частотам пиков и впадин).

При увеличении длины последовательности видим смещение пиков и изменение значений СПМ в оценке СПМ.

Таблица 2 – Классические методы параметрического спектрального анализа для АР-модели

Метод	Достоинства	Недостатки
Юла-Уолкера	Хороший результат при анализе "длинных" последовательностей. Гарантирует устойчивость БИХ-фильтра, соответствующего АР-модели	Для "коротких" последова- тельностей завышенный порядок АР-модели может сопровождаться смещением и расщеплением пиков
Бёрга	Хороший результат при анализе "длинных" последовательностей и удовлетворительный при анализе "коротких" последовательностей. Гарантирует устойчивость БИХ-фильтра, соответствующего АР-модели	Для "коротких" последова- тельностей завышенный порядок АР-модели может сопровождаться смещением и расщеплением пиков
Ковариационный	Более высокая точность при анали- зе "коротких" последовательностей по сравнению с методом Юла—Уолкера с тем же порядком АР-модели	Требуют проверки фильтра на устойчивость БИХ-фильтра, соответствую- щего АР-модели
Модифицированный ковариационный	Более высокая точность при анали- зе "коротких" последовательностей по сравнению с методом Юла—Уолкера с тем же порядком АР-модели. Как правило, не приводит к расще- плению пиков и по сравнению с ковариационным методом обес- печивает их меньшее смещение	Требуют проверки фильтра на устойчивость БИХ-фильтра, соответствую- щего АР-модели