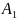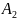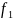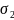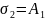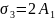цос 2сем / Obrazets_otcheta_LR16 (1)

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Федеральное государственное образовательное бюджетное учреждение

высшего образования

«Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М. А. Бонч-Бруевича»

_____________________________________________________________________________

Кафедра радиотехники

Дисциплина «Цифровая обработка сигналов»

Лабораторная работа № 16

СПЕКТРАЛЬНЫЙ АНАЛИЗ: НЕПАРАМЕТРИЧЕСКИЕ МЕТОДЫ

Выполнили: ст. гр. РТ-2x

№_бр 13

Проверил: ассистент каф. РТ,

Бойко И.А. ______

Санкт-Петербург

2024

СОДЕРЖАНИЕ ОТЧЕТА

ТАБЛИЦА ИСХОДНЫХ ДАННЫХ

Переменная	Назначение	Значение	Идентификатор
	Номер бригады		Nb = 13
	Период (длина) последовательности		N = 128
	Частота дискретизации		Fs = 8000
	Амплитуды дискретных гармоник		A1 = 0.93
			A2 = 1.395
	Частоты дискретных гармоник		f1 = 1000
			f2 = 2000
	Значения СКО		Вектор sigma = [0 0.93 1.86 2.79]

Формула СПМ

1. Свойства СПМ:

1. СПМ – четная функция

2. СПМ – вещественная функция частоты

3. СПМ – Неотрицательная функция частоты

4. Взаимная спектральная плотность для стационарных случайных процессов

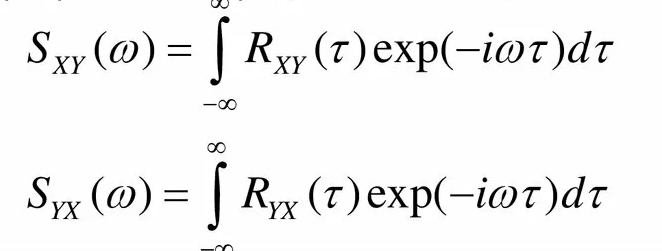
Теорема Винера-Хинчина (формула)

2. смысл всех переменных:

СПМ S(w) есть Фурье изображение АКФ R_x(m) последовательности x(n), теоретически бесконечной длины

Классические методы непараметрического спектрального анализа включают в себя (+ формулы вычисления спектрограмм):

Непараметрические методы:

• Метод периодограмм

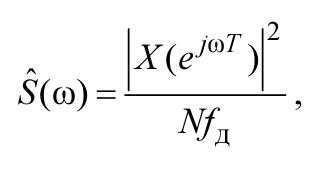
где — спектральная плотность конечной последовательности x(n)

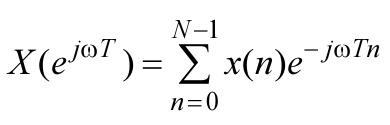
• Методы модифицированных периодограмм:

• метод периодограмм Даньелла

• метод периодограмм Бартлетта

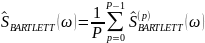
• метод периодограмм Уэлча

• Метод Блэкмана-Тьюки (коррелограмм)

п.1. Проверка информативности периодограммы в зависимости от уровня шума

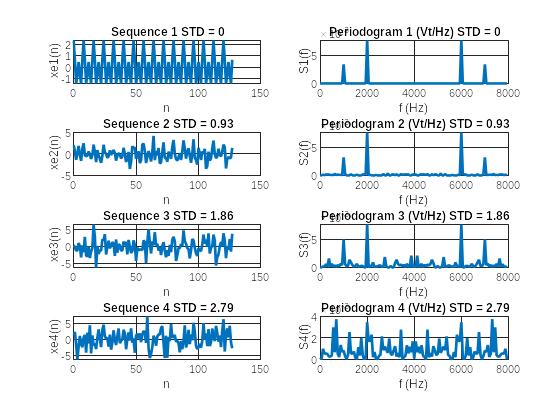
Рис. 1 Графики последовательностей и периодограмм с различными СКО шума

Пояснить:

• влияние уровня шума на информативность периодограммы;

При увеличении уровня шума, появляются дополнительные составляющие гармоник => подает информативность

• при каком уровне шума невозможно визуальное различение гармоник.

2.79

п.2. Проверка информативности периодограммы в зависимости от периода дискретизации по частоте

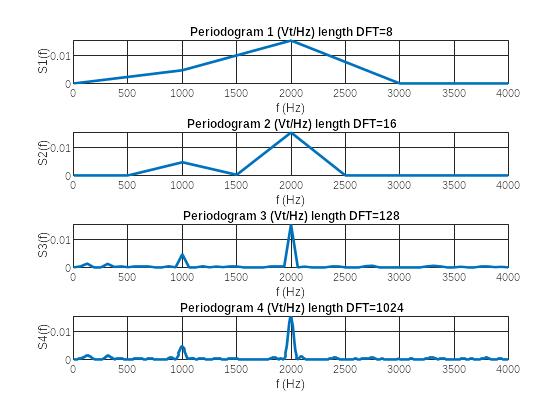
Рис. 2 Графики периодограмм при различной размерности ДПФ

Пояснить:

• чему равно разрешение по частоте при заданных размерностях ДПФ;

• при какой размерности ДПФ и почему периодограмма оказалась неинформативной;

При несовпадении размерности ДПФ и длины исходной последовательности по следняя автоматически дополняется нулями или усекается до длины Nfft.

При размерностях ДПФ меньше 128 периодограмма оказалась неинформативная

• при какой размерности ДПФ периодограмма наиболее информативна (наиболее узкая и гладкая и содержит обе гармоники).

При ДПФ = 1024

п.3. Проверка оценки СПМ на асимптотическую несмещенность и состоятельность

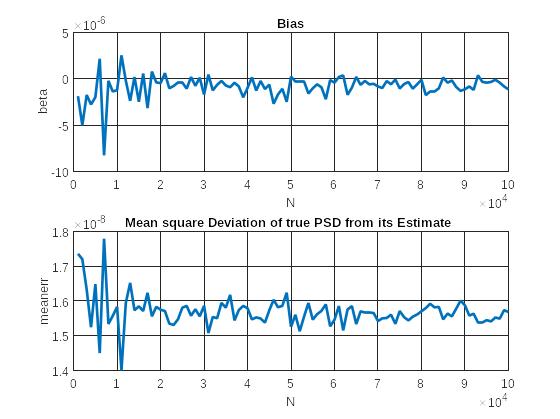
Рис. 3 Графики зависимости смещения и среднего квадрата отклонения истинной СПМ от ее оценки

Сделать вывод об оценке СПМ нормального белого шума (смещенная, асимптотически несмещенная, состоятельная, несостоятельная).

По графику 1 СПМ нормального белого шума является несмещённой (т.к смещение стремится к нулю), а по графику 2 – несостоятельной (т.к квадрат отклонения истинной СПМ не стремится к нулю).

п.4. Формирование случайной последовательности с требуемой АКФ

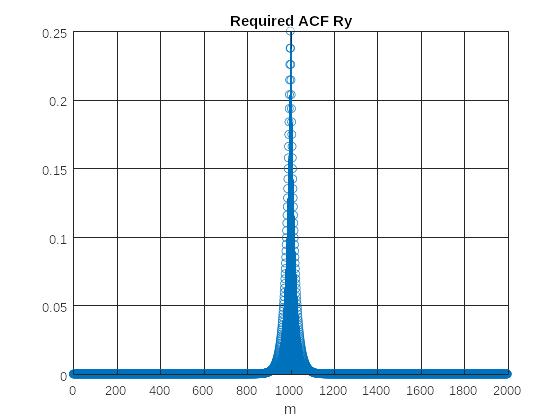
Рис. 4 График требуемой АКФ

Четный порядок КИХ-фильтра:

R = 160

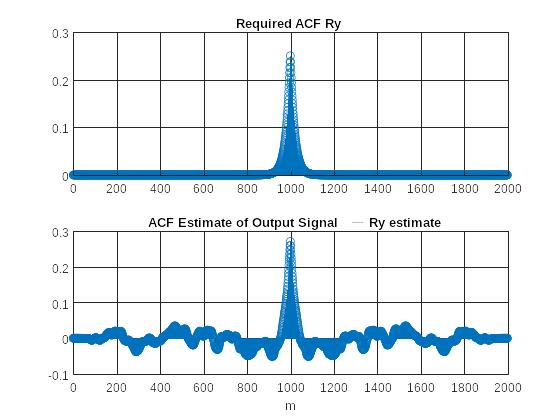
Рис. 5 Графики требуемой АКФ и оценки АКФ реакции

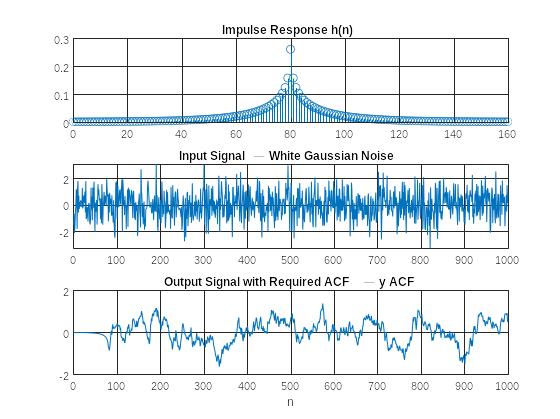
Рис. 6 Графики ИХ, нормального белого шума и реакции КИХ-фильтра

Пояснить:

• какой тип КИХ-фильтра выбран и почему;

Требуемая АКФ совпадает с АКФ ИХ с точностью до множителя. Однако быстро затухающую АКФ можно представить как АКФ ИХ, дополненную справа и слева нулями до длины L = 2N - 1, где R<<N. В этом случае порядок R будет равен длине требуемой АКФ от ее центрального отсчета до ближайшего отсчета, значение которого близко к нулю. В данном случае R=160.

• что используется в качестве воздействия КИХ-фильтра;

Нормальный белый шум

• что собой представляет реакция КИХ-фильтра.

Случайную последовательность длины N с требуемой АКФ на выходе КИХ-фильтра

п.5. Фильтрация случайной последовательности с требуемой АКФ

Рис. 7 Графики исходной и преобразованной последовательностей

Пояснить:

• что называют трендом во временной области;

Низкочастотные составляющие

п.6. Расчет периодограммы

Рис. 8 Графики периодограммы

п.7. Расчет периодограммы Даньелла

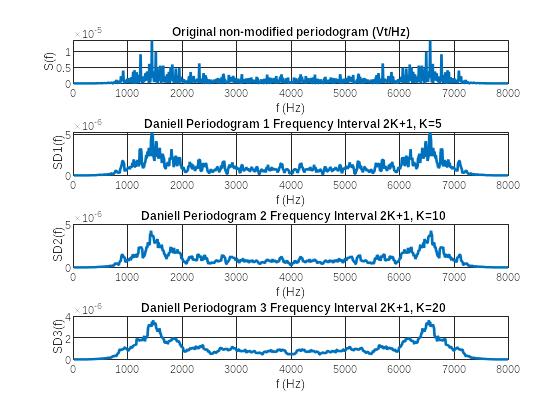
Рис. 9 Графики периодограмм Даньелла

Пояснить:

• при каком значении K периодограмма Даньелла наименее осциллирующая;

При K=20 периодограмма Даньелла наименее осцилирующая;

• как изменилась интенсивность осцилляций периодограммы Даньелла по сравнению с периодограммой.

Интенсивность осцилляций периодограммы Даньелла меньше по сравнению с периодограммой.

п.8. Расчет периодограммы Бартлетта

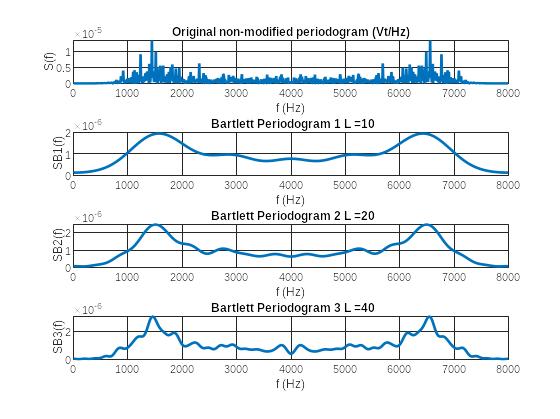
Рис. 10 Графики периодограммы Бартлетта

Пояснить:

• при какой длине фрагмента L периодограмма Бартлетта наименее осциллирующая;

При L=10 периодограмма Бартлетта наименее осциллирующая;

• как изменилась интенсивность осцилляций периодограмм Бартлетта по сравнению с периодограммами Даньелла.

Интенсивность осцилляций периодограммы Бартлетта уменьшилась по сравнению с периодограммой Даньелла.

п.9. Расчет периодограммы Уэлча

Рис. 11 Графики периодограммы Уэлча

Пояснить:

• при какой длине фрагмента L периодограмма Уэлча наименее осциллирующая;

При L=25 периодограмма Бартлетта наименее осциллирующая

• как изменилась интенсивность осцилляций периодограмм Уэлча по сравнению с периодограммой и периодограммами Даньелла и Бартлетта.

Интенсивность осцилляций периодограммы Уэлча уменьшилась по сравнению с периодограммой Даньелла и увеличилась по сравнению с периодограммой Бартлетта.

п.10. Расчет оценки СПМ по методу Блэкмана-Тьюки

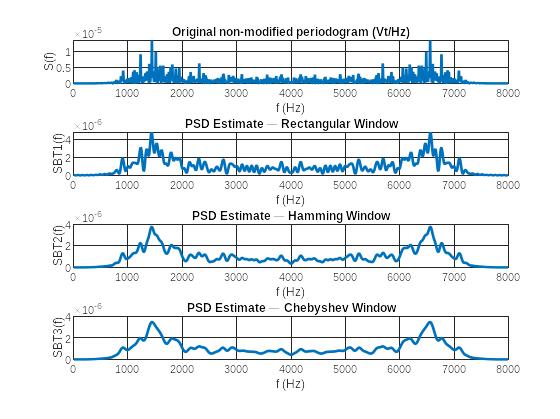
Рис. 12 Графики оценки СПМ, вычисленных по методу Блэкмана-Тьюки

Пояснить:

• при каком окне оценка СПМ по методу Блэкмана—Тьюки наименее осциллирующая;

При окне Чебышева

• как изменилась интенсивность осцилляций оценки СПМ по методу Блэкмана—Тьюки по сравнению с периодограммой и периодограммами Даньелла, Бартлетта и Уэлча.

Интенсивность осцилляции увеличилась в сравнении с Бартлетта и Уэлча, но в сравнении с Даньелла уменьшилась

п.11. Определение показателей качества оценок СПМ

Значения СКО:

СКО периодограммы: STD_S = 1.364067829231598e-06

СКО периодограмм ДАНЬЕЛЛА при различном количестве усредняемых частот K:

STD_SD =

5.000000000000000 0.000000864599750

10.000000000000000 0.000000796549846

20.000000000000000 0.000000754796208

СКО периодограмм БАРТЛЕТТА при различной длине фрагмента L:

STD_SB =

1.0e+02 *

1.000000000000000 0.000000005147263

0.500000000000000 0.000000006268455

0.250000000000000 0.000000006831063

СКО периодограммы УЭЛЧА при различной длине фрагмента L и величине перекрытия Q

STD_SW =

1.0e+02 *

1.000000000000000 0.130000000000000 0.000000007777568

0.500000000000000 0.130000000000000 0.000000007799032

0.250000000000000 0.130000000000000 0.000000006657996

СКО оценок СПМ по методу БЛЭКМАНА-ТЬЮКИ при различных окнах

STD_SBT =

3×2 cell array

{'Rectangular Window'} {[8.474894539578079e-07]}

{'Hamming Window' } {[7.747533268327145e-07]}

{'Chebyshev Window' } {[7.546337497945203e-07]}

Значения добротности:

ДОБРОТНОСТЬ периодограммы: Q_S = 0.5120

ДОБРОТНОСТЬ периодограмм ДАНЬЕЛЛА при различном количестве усредняемых частот K:

Q_SD =

5.0000 1.2745

10.0000 1.5016

20.0000 1.6723

ДОБРОТНОСТЬ периодограмм БАРТЛЕТТА при различной длине фрагмента L

Q_SB =

100.0000 3.5960

50.0000 2.4246

25.0000 2.0417

ДОБРОТНОСТЬ периодограмм УЭЛЧА при различной длине фрагмента L и величине перекрытия Q

Q_SW =

100.0000 13.0000 1.5474

50.0000 13.0000 1.6813

25.0000 13.0000 2.2130

ДОБРОТНОСТЬ оценок СПМ по методу БЛЭКМАНА-ТЬЮКИ при различных окнах

Q_SBT =

3×2 cell array

{'Rectangular Window'} {[1.3265]}

{'Hamming Window' } {[1.5872]}

{'Chebyshev Window' } {[1.6730]}

Пояснить:

• какая из оценок СПМ является наилучшей и наихудшей по критериям СКО и добротности;

Наилучшая из оценок СПМ у периодограммы Бартлетта (СКО и добротность);

Наихудшая из оценок СПМ у периодограммы (СКО и добротность).

• соответствие между показателями качества и графиками оценок СПМ.

Показатели качества соответствуют графикам оценок СКО)

п.12. Построение спектрограммы

Рис. 13 Графика спектрограммы дискретного гармонического сигнала

Пояснить, с какой целью строится спектрограмма:

• Спектрограмма строится для наблюдения мгновенного спектра, зависящего от времени. Само значение СПМ отображается цветом (по шкале: сверху максимальное значения СПМ, снизу минимальное)

Таблица 2 – Классические методы непараметрического спектрального анализа

Метод	Достоинства	Недостатки
Периодограмм	высокая разрешающая способность среди классических методов	Не является состоятельной оценкой спектральной плотности мощности. Дисперсия такой оценки сравнима с квадратом её математического ожидания. С ростом числа используемых отсчётов значения периодограммы начинают всё быстрее колебаться. Не обеспечивает усреднения, необходимого для анализа шумоподобных сигналов или даже синусоид при низком отношении сигнал/шум
Периодограмм Даньелла	Асимптотически несмещённая оценка спектральной плотности мощности (СПМ). Менее осциллирующая, чем исходная Фурье-периодограмма (за счёт усреднения по соседним частотам).	Ухудшение частотного разрешения (возможность различения двух близко расположенных частот гармоник) при увеличении степени сглаживания (длины окна). Таким образом, при использовании метода необходимо искать компромисс между уменьшением изрезанности оценки СПМ и ухудшением частотного разрешения. В методе периодограмм Даньелла сглаживание исходной (немодифицированной) периодограммы достигается за счёт её усреднения по соседним частотам.
Периодограмм Бартлетта	Даёт асимптотически состоятельную оценку энергетического спектра; Позволяет уменьшить дисперсию периодограммы в обмен на снижение разрешения по сравнению со стандартными периодограммами.	Сглаживание, вносимое окном Бартлетта, ограничивает способность периодограммы различать близко расположенные узкополосные составляющие спектра; Большие боковые лепестки прямоугольного окна могут привести к маскированию слабых узкополосных составляющих
Периодограмм Уэлча	Хорошее сглаживание сигналов; Использование окон (весовых функций) и частично перекрывающихся сегментов сигнала; Дисперсия оценки спектра мощности меньше, чем при методе Бартлетта	Возможная потеря острых пиков спектра; С ростом степени перекрытия увеличиваются вычислительные затраты и корреляция между отдельными подпоследовательностями
Блэкмана-Тьюки	Вычислительная эффективность. 2 Метод основан на использовании алгоритма быстрого преобразования Фурье (БПФ). Оценка СПМ прямо пропорциональна мощности синусоидальных процессов. 2	Подавление главных лепестков слабых сигналов боковыми лепестками сильных сигналов. Частотное разрешение ограничено длиной имеющейся записи анализируемых данных и не зависит от характеристик этих данных и их отношения сигнал/шум. Искажение спектра из-за просачивания энергии боковых лепестков. Необходимость псевдоусреднения по ансамблю для получения статистически состоятельных оценок спектров периодограмм. Появление отрицательных значений СПМ при использовании метода в случае, когда применяются некоторые автокорреляционные оценки последовательностей. 2

РАБОТА ЗАВЕРШЕНА.