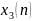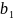Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Федеральное государственное образовательное бюджетное учреждение

высшего образования

«Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М. А. Бонч-Бруевича»

_____________________________________________________________________________

Кафедра радиотехники

Дисциплина «Цифровая обработка сигналов»

Лабораторная работа № 10

ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ (часть 2)

Выполнили: ст. гр. РТ-2x

№_бр 13

Проверил: ассистент каф. РТ,

Бойко И.А. ______

Санкт-Петербург

2024

СОДЕРЖАНИЕ ОТЧЕТА

ТАБЛИЦА ИСХОДНЫХ ДАННЫХ

Переменная	Назначение	Значение	Идентификатор
	Номер бригады		Nb = 13
	Период (длина) последовательности		N = 64
	Частота дискретизации		Fs = 8000
	Амплитуды дискретных гармоник		A1 = 1.13
			A2 = 2.26
	Частоты дискретных гармоник		f1 = 2000
			f2 = 3000
	Период последовательности		M = 71
	Частоты дискретных гармоник		f1_1 =2200
			f2_1 = 2140
	Частоты дискретных гармоник		f1_2 = 2100
			f2_2 = 2237.5
	Периодическая последовательность		Вектор x3 = [1.3 2.6 3.9 5.2 6.5]
	Периодическая последовательность		Вектор x4 = [6.5 5.2 3.9 2.6 1.30]
	Периодическая последовательность		Вектор x5 = [1.3 2.6 3.9]
	Периодическая последовательность		Вектор x6 = [3.9 2.6 1.3 2.6 3.9]
	Коэффициенты числителя передаточной функции		Вектор b = [0.76 9.878024 1.064]
	Коэффициенты знаменателя передаточной функции		Вектор a = [1.0000 -10,439 0,718]
	Длина ИХ		N1 = 23
	Длина воздействия		N2 = 33
	Длина воздействия		N3 = 203

……………………………………………………………………………………………….

ФОРМУЛЫ ДПФ:

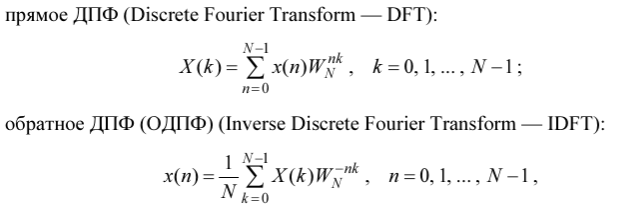
• с мысл всех переменных:

n – дискретное нормированное время:

N – период последовательности; длина последовательности

x(n) – N-точечная последовательность (один период);

X(k) – N-точечное ДПФ (один период).

k – дискретная нормированная частота:

- период дискретизации по частоте (разрешение по частоте)

- поворачивающий множитель

- k-я дискретная гармоника

• трактовка ДПФ для периодической последовательности:

Для периодической последовательности x(n) с периодом N ДПФ X(k) – это её спектр с точностью до множителя 1/N

• трактовка ДПФ для конечной последовательности:

Для конечной последовательности x(n) длины N ДПФ X(k) – это дискретные отсчеты её СП в N дискретных точках на периоде ω_Д

ПУНКТЫ ЗАДАНИЯ

п.1 Проверка равенства Парсеваля

Левая (e1) и правая (e2) часть равенства Парсеваля

E1 = 204.304 E2 = 204.304

Пояснить смысл равенства Парсеваля:

Равенство Парсеваля

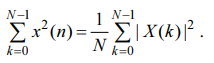
Теорема Парсеваля устанавливает равенство между энергией сигнала и энергией его спектра.

п.2 Исследование эффекта растекания спектра для одной дискретной гармоники

Число периодов дискретной гармоники с частотой f1

N = 64 --> P_N = 16

M = 71 --> P_M = 17.75

Рис.1 Графики амплитудных спектров

Пояснить:

• с какой целью определяется значение P ;

С целью проверить наличие эффекта растекания спектра.

• в каком случае и почему наблюдается растекание спектра.

При дробном P присутствует растекание спектра.

п.3. Исследование возможности уменьшения растекания спектра с помощью окна

Рис. 2 Графики амплитудных спектров до и после применения окна

Пояснить, что изменилось в результате применения окна:

Растекание спектра уменьшилось.

п.4. Исследование эффекта растекания спектра для суммы двух дискретных гармоник

Число периодов дискретных гармоник с частотами f1_1 и f2_1:

f1_1 = 2200 --> P1_1 = 17.6

f2_1 = 2140 --> P2_1 = 17.12

Рис. 3 Графики амплитудных спектров до и после применения окна

Пояснить причину растекания спектра и цель применения окна:

На интервал NT укладывается нецелое число периодов T при заданной частоте.

Окно применяется с целью уменьшить растекание спектра.

п.5. Улучшение различения дискретных гармоник с близко расположенными частотами

Период последовательности и частоты гармоник:

N = 64 f1_2 = 2100 f2_2 = 2237.5

Разрешение ПО ЧАСТОТЕ Delta_N = 125

Расстояние между ЧАСТОТАМИ Delta_f = 137.5

Длина последовательности L = 640

Период дискретизации по частоте Delta_L = 12.5

Рис.4 Графики n-точечного ДПФ и модуля спектральной плотности, восстановленной по L точкам

Частоты гармоник:

k_1 = 180 f_1 = 2250

k_2 = 166 f_2 = 2075

!!Определите ЧАСТОТЫ ГАРМОНИК по ГРАФИКУ

Пояснить:

• соответствуют ли близко расположенные частоты условию (10.2);

Соответствуют.

• соответствует ли выведенная длина L условию (10.3);

160

Соответствует.

• с какой погрешностью определены частоты и причину погрешности.

П ричина погрешности заключается в том, что частоты f1 и f2 могут быть некратными периоду

п.6. Вычисление круговой свертки

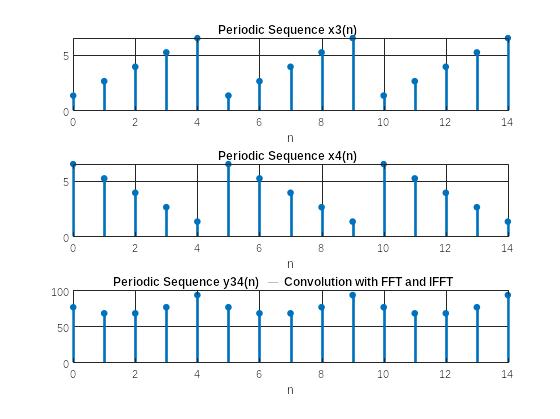
Рис. 5 Графиков последовательностей и круговой свертки (3 периода)

Записать формулу круговой свертки и пояснить алгоритм ее вычисления с помощью ДПФ:

п.7. Вычисление линейной свертки

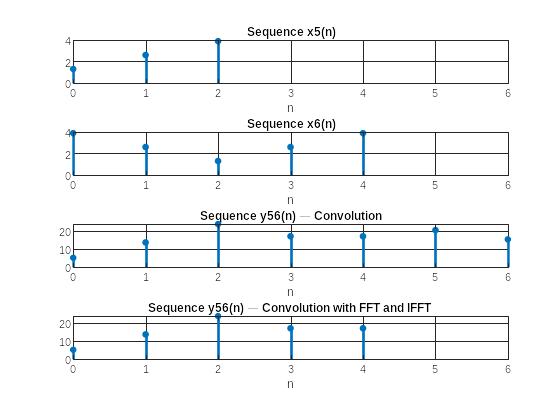
Рис. 6 Графики последовательностей и линейной свертки

Записать формулу линейной свертки и пояснить алгоритм ее вычисления с помощью ДПФ.

п.8. Вычисление реакции ЛДС по формуле свертки

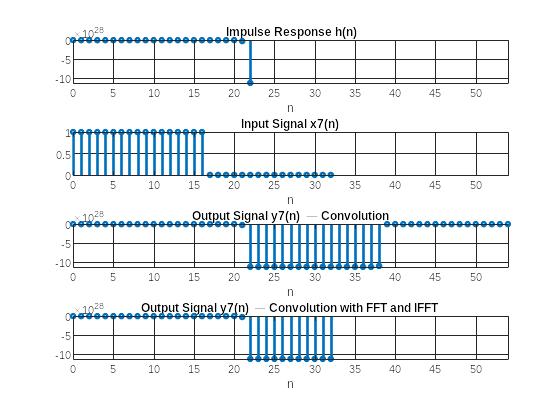
Рис.7 Графики ИХ, воздействия и реакции

Пояснить:

• преимущество вычисления реакции по формуле свертки с помощью ДПФ;

Для сокращения вычислительных затрат линейную свертку рассчитывают с помощью ДПФ

• чему равна длина реакции, вычисленной первым и вторым способами;

L1=60

L2=34

• в каком случае длину реакции необходимо ограничить до длины воздействия.

Ограничение длины реакции вводится с целью повысить стабильность системы.

п.9. Вычисление реакции ЛДС методом перекрытия с накоплением

Рис.8 Графики воздействия и реакции

Пояснить, в каком случае целесообразно вычислять реакцию методом перекрытия с накоплением.

При большой длине воздействия N2