Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Федеральное государственное образовательное бюджетное учреждение

высшего образования

«Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М. А. Бонч-Бруевича»

_____________________________________________________________________________

Кафедра радиотехники

Дисциплина «Цифровая обработка сигналов»

Лабораторная работа № 09

ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ (часть 1)

Выполнили: ст. гр. РТ-2x

№_бр 13

Проверил: ассистент каф. РТ,

Бойко И.А. ______

Санкт-Петербург

2024

СОДЕРЖАНИЕ ОТЧЕТА

ТАБЛИЦА ИСХОДНЫХ ДАННЫХ

Переменная	Назначение	Значение	Идентификатор
	Номер бригады		Nb = 13
	Период (длина) последовательности		N = 64
	Частота дискретизации		Fs = 8000
	Период дискретизации		1/Fs = 0.000125
	Амплитуды дискретных гармоник		A1 =1.13
			A2 = 2.26
	Частоты дискретных гармоник		f1 = 1000
			f2 = 3000

……………………………………………………………………………………………….

ФОРМУЛЫ ДПФ:

• с мысл всех переменных:

n – дискретное нормированное время:

N – период последовательности; длина последовательности

x(n) – N-точечная последовательность (один период);

X(k) – N-точечное ДПФ (один период).

k – дискретная нормированная частота:

- период дискретизации по частоте (разрешение по частоте)

- поворачивающий множитель

- k-я дискретная гармоника

• трактовка ДПФ для периодической последовательности:

Для периодической последовательности x(n) с периодом N ДПФ X(k) – это её спектр с точностью до множителя 1/N

• трактовка ДПФ для конечной последовательности:

Для конечной последовательности x(n) длины N ДПФ X(k) – это дискретные отсчеты её СП в N дискретных точках на периоде ω_Д

ПУНКТЫ ЗАДАНИЯ:

1. Вычисление амплитудного и фазового спектров периодической последовательности.

Исходных амплитуд и частот дискретных гармоник:

A1 = 1.13 A2 = 2.26

f1 = 1000 f2 = 3000

Рис.1 Графики периодической последовательности

Рис. 2 Графики амплитудного спектра периодической последовательности

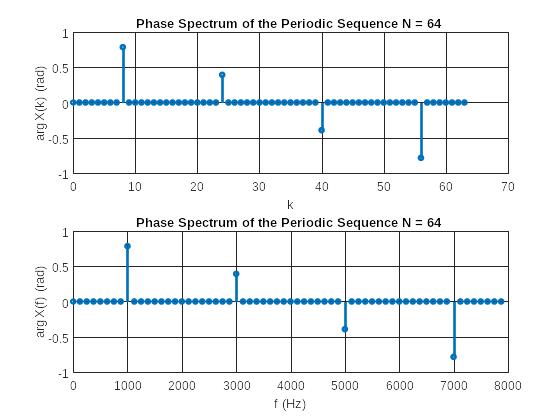
Рис. 3 Графики фазового спектра периодической последовательности

Пояснения:

• д искретное нормированное время – дискретное время, делённое на период повторения

• Связь частоты f (Гц) с дискретной нормированной частотой:

• Вид амплитудного и фазового спектров:

А мплитудный спектр вещественной периодической последовательности равен модулю ДПФ |X(k)| с точностью до множителя:

Аргумент arg{X(k)} — фазовым спектром периодической последовательности

2. Вычисление ДПФ конечной последовательности.

Рис. 4 Графики модуля ДПФ конечной последовательности и амплитудного спектра

Пояснить связь модуля ДПФ конечной последовательности с амплитудным спектром периодической последовательности:

Пояснения

Модуль ДПФ конечной последовательности от амплитудного спектра периодической последовательности различается в N раз.

3. Определение амплитуд и частот дискретных гармоник.

Выходные параметры функции fft_e:

MODm = 1.1300 2.2600 2.2600 1.1300

m = 8 24 40 56

Амплитуды и частоты дискретных гармоник:

A1 = 1.13 A2 = 2.26

k1 = 8 k2 = 24

f1 = 1000 f2 = 3000

Выходные параметры функции fft_e1 совпали с исходными

Пояснение:

• смысл выходных параметров function-файла fft_e1:

MODm — вектор значений модуля ДПФ полезного сигнала

m — вектор значений частот полезного сигнала

• Значения абсолютных частот дискретных гармоник связаны со значениями дискретных нормированных частот соотношением:

4. Граничные значения порогов для первого и второго критериев выделения полезного сигнала.

Граничные значения порога для ПЕРВОГО КРИТЕРИЯ: e1_low = 0.32993 e1_up = 1

Граничные значения порога для ВТОРОГО КРИТЕРИЯ: e2_low = 1.8349 e2_up = 16.8566

Первый критерий:

Нижнее граничное значение рассчитывается путем деления максимума амплитудного спектра шума на максимум амплитудного спектра смеси сигнала с шумом.

Верхнее граничное значение равняется единице.

Второй критерий:

Нижнее граничное значение рассчитывается путем деления квадрата максимума амплитудного спектра шума на среднюю мощность смеси сигнала с шумом.

Верхнее граничное значение рассчитывается путем деления квадрата максимума амплитудного спектра смеси сигнала с шумом на среднюю мощность смеси сигнала с шумом.

5. Выделение полезного сигнала по первому критерию.

Рис. 5 График аддитивной смеси сигнала с шумом

Рис. 6 Графики амплитудного и нормированного амплитудного спектров аддитивной смеси сигнала с шумом

При e1=0.5 выходные параметры функции fft_e1:

MODm =1.2794 2.0805 2.0805 1.2794

m = 8 24 40 56

Часть MODm выделенных по первому критерию, больше полученных в пункте 3. Частоты совпадают.

Пояснение:

• Значение порога ε1 было выбрано: e1=0.5

• смысл выходных параметров function-файла fft_e1:

MODm — вектор значений модуля ДПФ полезного сигнала

m — вектор значений частот полезного сигнала

• MODm = 1.2115 2.3453 2.3453 1.2115

• Применение первого критерия неэффективно в случае невыполнении условия

6. Выделение полезного сигнала по второму критерию.

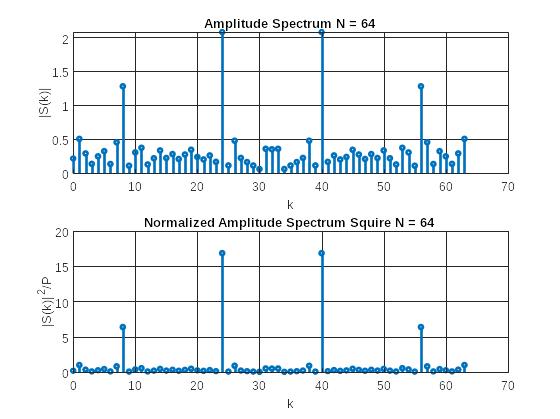
Рис. 7 Графики амплитудного спектра и квадрата амплитудного спектра, нормированного к величине средней мощности аддитивной смеси сигнала с шумом

При e2=10 выходные параметры функции fft_e2:

MODm = 2.0805 2.0805

m = 24 40

Часть гармоник было утеряно, а оставшиеся амплитуды ниже исходных. Частоты совпадают.

Пояснения:

• Значение порога ε2 = 10

• смысл выходных параметров function-файла fft_e2:

MODm — вектор значений модуля ДПФ полезного сигнала

m — вектор значений частот полезного сигнала

• Полезному сигналу согласно второму критерия соответствуют вторые гармоники

7. Восстановление аналогового сигнала.

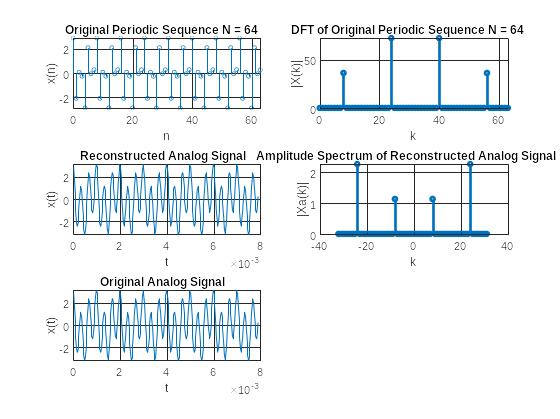
Рис. 8 Графики последовательности и модуля ее ДПФ, восстановленного аналогового сигнала, его спектра и исходного аналогового сигнала

Пояснения:

• Модуль ДПФ последовательности связан со спектром аналогового сигнала по формуле: MODa = (2/N)*abs(Xa), где Xa - спектр аналогового сигнала.

• Визуально восстановленный и оригинальный сигнал совпадают

8. Восстановление спектральной плотности конечной последовательности.

Рис. 9 Графики ДПФ и спектральной плотности конечной последовательности, вычисленной двумя способами

Пояснение:

• связь между ДПФ и спектральной плотностью:

• Спектральная плотность высчитывается по формуле: S=

на каждом отсчете

• Дискретные нормированные частоты в 10 раз больше частот спектральной плотности

9. Уменьшение периода дискретизации по частоте при вычислении ДПФ.

Рис. 10 Графики конечных последовательностей, ДПФ и спектральных плотностей

Периоды ДПФ и периоды дискретизации по частоте:

L = [64 128 256]

Delta_f = [125 62.5 31.25]

Пояснение

• Причина изменения периода дискретизации по частоте:

• Разрешение по частоте изменяется, уменьшается. (Разрешение по частоте — период дискретизации по частоте)

• Разрешение по частоте: Delta_f = [125 62.5 31.25]

• Уменьшение периода дискретизации по частоте до , не меняет разрешения по частоте, а лишь улучшает условия различения близко расположенных частот дискретных гармоник.

9