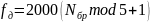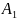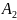цос 2сем / Obrazets_otcheta_LR21 (1)

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Федеральное государственное образовательное бюджетное учреждение

высшего образования

«Санкт-Петербургский государственный университет телекоммуникаций

им. проф. М. А. Бонч-Бруевича»

_____________________________________________________________________________

Кафедра радиотехники

Дисциплина «Цифровая обработка сигналов»

Лабораторная работа № 21

АДАПТИВНЫЕ ФИЛЬТРЫ

Выполнили: ст. гр. РТ-2x

№_бр 13

Проверил: ассистент каф. РТ,

Бойко И.А. ______

Санкт-Петербург

2024

СОДЕРЖАНИЕ ОТЧЕТА

ТАБЛИЦА ИСХОДНЫХ ДАННЫХ

Переменная	Назначение	Значение			Идентификатор
	Номер бригады				Nb = 13
	Длина КИХ-фильтра в составе АФ				L = 44
	Длина входного сигнала				L = 4000
	Частота дискретизации				Fs = 8000
	Амплитуды дискретных гармоник				A1 = 0.043
					A2 = 0.0215
	Частоты дискретных гармоник				f1 = 1000
					f2 = 2000
	Заданные (истинные) параметры АР-модели					Вектор a = [1 -0.1 0.2 0.2 0.1 0.3]
		1	1	1
		-0.86	-0.1	0.5
		0.54	0.2	0.17
		-0.3	0.2	0.3
		-0.17	0.1	0.1
		0.22	0.3	0.1
		-0.1	—	-0.1
		—	—	-0.5

Структура адаптивного фильтра

Адаптивным фильтром (АФ) называют систему, параметры которой адаптируются (подстраиваются) к сигналу с заранее неопределенной статистической моделью в процессе его обработки.

Адаптивный фильтр включает в себя:

• КИХ-фильтр;

• алгоритм адаптации.

Рис.1. Структурная схема линейного адаптивного фильтра с обратной связью.

x(n) – входной сигнал, заранее неизвестный;

d(n) – образцовый сигнал, заранее известный.

На выходе АФ формируются два сигнала:

• y(n) – выходной сигнал;

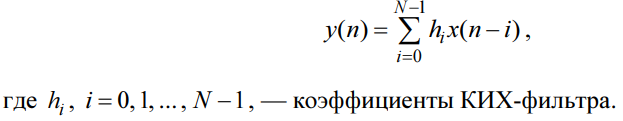
Коэффициенты РУ КИХ-фильтра совпадают с отсчётами его ИХ.

• e(n) – сигнал ошибки.

КИХ-фильтр представляет собой ЛДС (условие аддитивности и однородности), однако в процессе адаптивной фильтрации параметры АФ (набор коэффициентов КИХ-фильтра) изменяются во времени, следовательно, АФ нелинейная система обработки сигналов.

В АФ под обратной связью понимают связь алгоритма адаптации с сигналом ошибки, на основе которого подстраиваются коэффициенты КИХ-фильтра. Устойчивость алгоритма адаптации – сходимость вычисляемых параметров АФ к оптимальным параметрам (для КИХ-фильтра устойчивость гарантируется).

Основной задачей адаптивной фильтрации является обеспечение наилучшего приближения выходного сигнала y(n) к образцовому сигналу d(n) по заданному критерию. Основная сложность в проектировании АФ – разработка алгоритмов фильтрации.

п.1. Моделирование нормального белого шума

Созданная модель НОРМАЛЬНОГО БЕЛОГО ШУМА длины L(4000) с нулевым МО и единичной дисперсией (r_gauss=randn(1,L)) будет использована в дальнейших исследованиях

п.2. Моделирование структуры АФ с алгоритмом LMS

Создаём модель структуры АФ с алгоритмом LMS в виде объекта adaptfilt.lms с именем Hlms (Hlms=adaptfilt.lms(N,mu)).

Пояснение:

- Какой из входных параметров объекта adaptfilt.lms соответствует шагу адаптации и как он определяется

N=50; средний квадрат входного сигнала Px=var(x); максимальный шаг адаптации mu_max=2/(N*Px); заданный шаг адаптации mu=0.5*mu_max;

- Свойства объекта adaptfilt.lms.

Свойства adaptfilt.lms: Algorithm – структура КИХ-фильтра и алгоритм адаптации; FilterLength – значение параметра N; StepSize – значение параметра step; Leakage – значение коэффициента утечки (0 до 1); PersistentMemory – начальные условия states, значение false – ННУ.

п.3. Моделирование структуры АФ с алгоритмом NLMS

Hnlms = adaptfilt.nlms(N,1,1,epsilon)

Пояснение:

- Какой из входных параметров объекта adaptfilt.nlms соответствует констан те ε и что она определяет;

Константа, определяющая максимальный шаг адаптации epsilon=1e-6;

- Свойства объекта adaptfilt.nlms.

Свойства объекта adaptfilt.nlms дублируют свойства объекта adaptfilt.lms и дополнительно включает в себя: Offset – константа epsilon, по умолчанию =0.

п.4. Моделирование структуры АФ с алгоритмом RLS

Hrls=adaptfilt.rls(N)

Пояснение:

- Какой из входных параметров объекта adaptfilt.rls соответствует коэффи циенту забывания λ в (21.53)—(21.54) и с какой целью он вводится;

Коэффициент забывания lambda по умолчанию =1 (позволяет учитывать предшествующие отсчёты входного сигнала с экспоненциально меньшим весом);

- Свойства объекта adaptfilt.rls.

Свойства объекта adaptfilt.rls: Algorithm – структура КИХ-фильтра и алгоритм адаптации; FilterLength – значение параметра N; Forgettingfactor – значение параметра lambda; Leakage – значение коэффициента утечки (0 до 1); PersistentMemory – начальные условия states, значение false – ННУ.

п.5. Оценка импульсной характеристики неизвестной ЛДС

Вычисление оценки ИХ неизвестной ЛДС включает шаги:

Моделирование входного сигнала неизвестной ЛДС — входного сигнала АФ x(n) в виде нормального белого шума r(n) ;

Моделирование неизвестной ЛДС — КИХ-фильтра ФНЧ порядка R1=int(N/2) с нормированной частотой разрыва = 0.5;

Вычисление выходного сигнала неизвестной ЛДС — образцового сигнала АФ d(n) с помощью функции – filter;

Вычисление истинной ИХ неизвестной ЛДС

Моделирование структур АФ — объектов adaptfilt с именами Hlms и Hrls;

Вычисление выходного сигнала y(n) и сигнала ошибки e(n) АФ с именем Hlms и АФ с именем Hrls с помощью функции filter;

Оределение параметров АФ с именами Hlms и Hrls – оценок ИХ неизвестной ЛДС .

Повторяем процедуру для другой неизвестной ЛДС – БИХ-фильтра ФВЧ Баттерворта порядка R1=int(N/2) с нормированной частотой среза =0.3

5.1. Оценка импульсной характеристики неизвестной ЛДС — КИХ-фильтра ФНЧ (FIR)

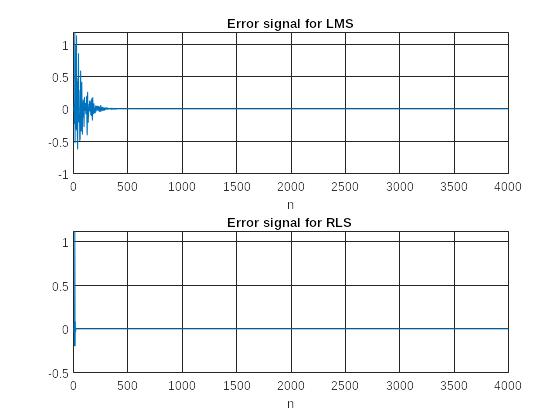
Рис. 1 Графики сигнала ошибки АФ

Рис. 2 Графики истинной импульсной характеристики (FIR) и её оценок

Среднее абсолютное отклонение отсчетов импульсной характеристики от ее оценок (FIR):

norm1_lms = 0.47838 norm1_rls = 2.8188e-17

5.2. Оценка импульсной характеристики неизвестной ЛДС — БИХ-фильтра ФВЧ (IIR)

Рис. 3 Графики сигнала ошибки АФ

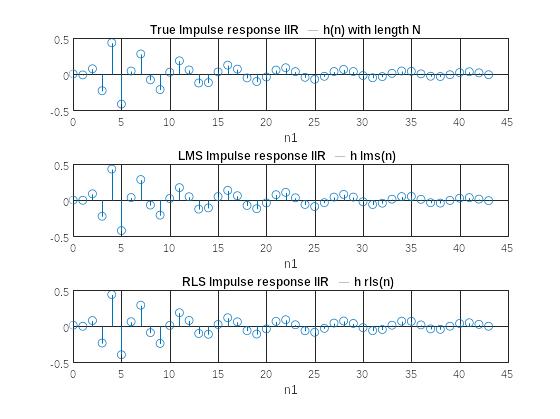
Рис. 4 Графики истинной импульсной характеристики (IIR) и ее оценок

Среднее абсолютное отклонение отсчетов импульсной характеристики от ее ОЦЕНОК (IIR): norm1_lms = 0.43314 norm1_rls = 0.010463

Пояснение:

- На основе какой системы решается задача оценки ИХ неизвестной ЛДС;

Задача оценки импульсной характеристики (ИХ) неизвестной системы, в предположении, что она представляет собой ЛДС (КИХ- или БИХ-фильтр), в условиях случайного воздействия сводится к решению задачи прямой идентификации. При прямой идентификации АФ – модель неизвестной системы.

Рис.6. Структурная схема идентификации систем: прямой(а), обратной(б).

- На каком интервале дискретного нормированного времени определяются оценки ИХ неизвестной ЛДС;

По завершении процесса адаптации ИХ КИХ-фильтра в составе АФ будет оценкой ИХ неизвестной системы на интервале дискретного нормированного времени, равном длине КИХ-фильтра.

- Какой из алгоритмов (LMS или RLS) обеспечивает более точную оценку ИХ по заданному критерию;

Более точную оценку ИХ по заданному критерию обеспечивает алгоритм RLS.

- Какой из неизвестных ЛДС (КИХ или БИХ) соответствует сигнал ошибки АФ с большей дисперсией.

Сигнал ошибки с большей дисперсией соответствует неизвестной ЛДС БИХ.

п.6. Очистка сигнала от шума

Моделирование процесса очистки сигнала от шума включает шаги:

Моделирование входного сигнала неизвестной ЛДС — входного сигнала АФ x(n)=x_ш(n). В качестве шума x_ш(n) – нормальный белый шум r(n);

Моделирование неизвестной ЛДС — КИХ-фильтра ФНЧ, искажающего шум x_ш(n), и вычисление его реакции с помощью функции filter;

Моделирование полезного сигнала s(n) в виде периодической последовательности (суммы двух гармоник) с периодом L :

Моделирование выходного сигнала неизвестной ЛДС — образцового сигнала АФ d(n) в виде аддитивной смеси сигнала s(n) с искаженным шумом :

Моделирование структур АФ — объектов adaptfilt с именами Hlms и Hrls;

Вычисление выходного сигнала y(n) и сигнала ошибки e(n) АФ с именем Hlms и АФ с именем Hrls с помощью функции filter.

Рис. 5 Графики полезного сигнала, его аддитивной смеси с шумом и оценок полезного сигнала (LMS) И (RLS)

Рис. 6 Графики амплитудных спектров полезного сигнала, его аддитивной смеси с шумом и оценок полезного сигнала (LMS) И (RLS) в установившемся режиме

Значения RMSE:

RMSE_lms = 0.056524 0.079952 0.056524 0.052832 0.057127 0.052832 0.057127 0.052832…

RMSE_rls = 0.058727 0.08143 0.058727 0.055391 0.059535 0.055391 0.059535 0.055391…

Пояснение:

- На основе какой системы решается задача очистки сигнала от шума;

Задача очистки сигнала от шума – задача прямой идентификации. Оценка полезного сигнала – сигнал ошибки e(n)

Рис.9.Структурная схема прямой идентификации при очистке сигнала от шума.

- Как по графику сигнала ошибки АФ оценить длительность переходного процесса в АФ;

Длительность переходного процесса можно оценить по графикам сигналов ошибки АФ; переходный процесс идет до момента, когда сигнал ошибки становится установившемся значением (перестаёт сильно осциллировать);

- Какой из алгоритмов (LMS или RLS) обеспечивает лучшую очистку сигнала от шума (по результатам визуального сравнения амплитудных спектров и значениям RMSE).

Алгоритм LMS в данном случае обеспечивает лучшую чистку сигнала от шума.

п.7. Выравнивание частотной характеристики неизвестной ЛДС

Моделирование выравнивания частотной характеристики неизвестной ЛДС включает шаги:

• моделирование входного сигнала неизвестной ЛДС — образцового сигнала АФ d(n);

В качестве входного сигнала неизвестной ЛДС d(n) выбираем аддитивную смесь сигнала s(n) с нормальным белым шумом r(n) с СКО, равным 3max{A1,A2} :

Для сигнала s(n) оставить неизменной частоту f1, а частоту f2 задать равной f2 = 3f1;

• Моделирование задержанного образцового сигнала d(n-D) посредством обнуления D=int(N/2) начальных значений сигнала d(n) ;

• Моделирование неизвестной ЛДС — КИХ-фильтра ФНЧ порядка R2=int(N/7) с нормированной частотой разрыва c = 0,5;

• Вычисление выходного сигнала неизвестной ЛДС — входного сигнала АФ x(n) с помощью функции filter;

• Вычисление выходного сигнала АФ y(n)= и сигнала ошибки e(n) с помощью функции filter;

• Определение параметров АФ — ИХ h(n) его КИХ-фильтра;

• Вычисление ИХ v(n)=g(n)*h(n) каскадного соединения неизвестной ЛДС и АФ h(n) .

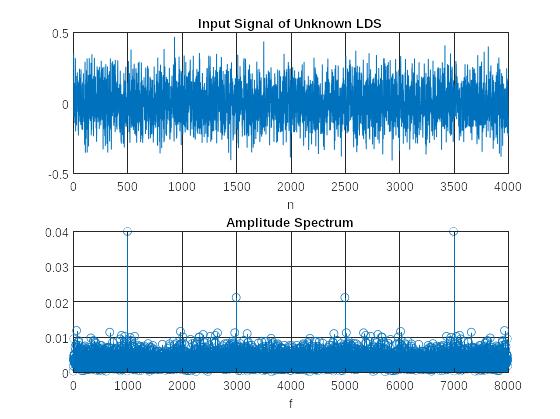
Рис. 7 Графики входного сигнала неизвестной ЛДС и его амплитудного спектра

Рис. 8 Графики выходного сигнала неизвестной ЛДС и его амплитудного спектра

Рис. 9 Графики импульсных характеристик неизвестной ЛДС, КИХ-фильтра в составе АФ и ИХ каскадного соединения

Рис. 10 Графики АЧХ неизвестной ЛДС, КИХ-фильтра в составе АФ и ИХ каскадного соединения

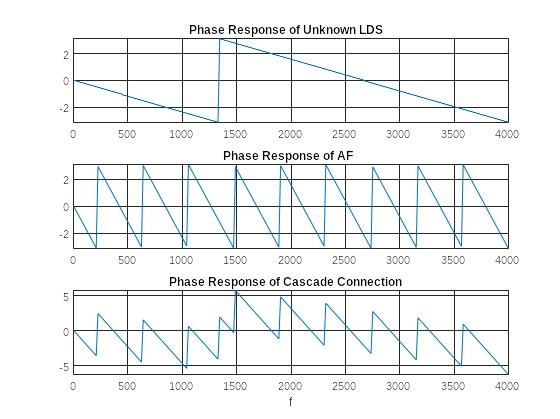
Рис. 11 Графики ФЧХ неизвестной ЛДС, КИХ-фильтра в составе АФ и ИХ каскадного соединения

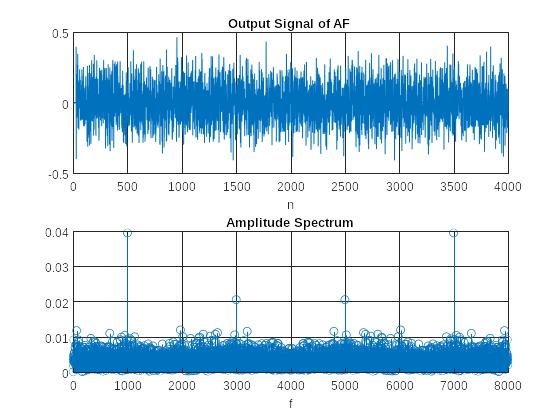
Рис. 12 Графики выходного сигнала АФ и его амплитудного спектра

Пояснения:

- На основе какой системы решается задача выравнивания частотной характеристики неизвестной ЛДС;

В качестве модели неизвестной системы с ограниченной полосой пропускания предлагается выбрать КИХ-фильтр ФНЧ или ПФ с симметричной ИХ. Подключение к выходу неизвестной системы АФ скомпенсирует искажения, вносимые неизвестной системой (АЧХ каскадного соединения неизвестной системы и АФ окажется более широкополосной, чем АЧХ неизвестной системы). Это и есть выравнивание частотной характеристики неизвестной системы;

Такая задача сводится к решению задачи обратной идентификации

Рис.16. Структурная схема обратной идентификации для выравнивания частотной характеристики неизвестной системы с ограниченной полосой пропускания.

- Чему равны частоты дискретных гармоник входного сигнала неизвестной ЛДС;

Частоты дискретных гармоник входного сигнала неизвестной ЛДС равны f1, а f2=3f1;

- Вид амплитудного спектра входного сигнала неизвестной ЛДС;

Амплитудный спектр входного сигнала неизвестной ЛДС зашумлён (смесь с шумом);

- Какому сигналу АФ соответствует входной сигнал неизвестной ЛДС;

Входной сигнал неизвестной ЛДС d(n), задержанный на D отсчётов – d(n-D) соответствует образцовому сигналу АФ (значение D=int(N/2));

- Вид амплитудного спектра выходного сигнала неизвестной ЛДС и причину его изменения относительно амплитудного спектра входного сигнала;

В амплитудном спектре выходного сигнала неизвестной ЛДС подавляется одна из спектральных составляющих сигнала, вследствие ограниченной полосы пропускания неизвестной системы;

- Вид импульсных характеристик неизвестной ЛДС, КИХ-фильтра в составе АФ и их каскадного соединения;

Импульсные характеристики неизвестной ЛДС, КИХ-фильтра в составе АФ и их каскадного соединения симметричные;

- Какому виду ИХ соответствует выровненная АЧХ

Выровненная АЧХ (ФНЧ) соответствует симметричной ИХ; ИХ каскадного соединения близка к виду цифрового единичного импульса;

- Вид ФЧХ неизвестной ЛДС, КИХ-фильтра в составе АФ и их каскадного со единения

ФЧХ неизвестной ЛДС, КИХ-фильтра в составе АФ и их каскадного соединения линейные;

- Результат сравнения амплитудных спектров выходного сигнала неизвестной ЛДС и выходного сигнала АФ.

В ходе сравнения амплитудных спектров выходного сигнала неизвестной ЛДС и выходного сигнала АФ можно заметить, что спектральная составляющая восстановлена.

п.8. Вычисление оценок параметров АР-модели и оценок параметров линейного предсказания

Вычисление оценок параметров АР-модели и оценок параметров линейного предсказания включает шаги:

Моделирование входного сигнала АР-модели — нормального белого шума ;

Задание вектора a известных параметров АР-модели (известных параметров линейного предсказания);

Вычисление выходного (моделируемого) сигнала АР-модели ;

Вычисление оценок параметров АР-модели 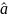методом Юла—Уолкера в предположении, что анализируемый сигнал x(n) совпадает с моделируемым сигналом :

Моделирование структуры АФ — объекта adaptfilt с именем Hrls;

Моделирование образцового сигнала АФ d(n), совпадающего с анализируемым сигналом x(n):

Моделирование входного сигнала АФ — задержанного сигнала x(n-1) посредством обнуления первого отсчета сигнала x(n);

Вычисление выходного сигнала АФ y(n-1) и сигнала ошибки e(n) c помощью функции filter;

Определение параметров АФ с противоположным знаком — вектора оценок параметров линейного предсказания.

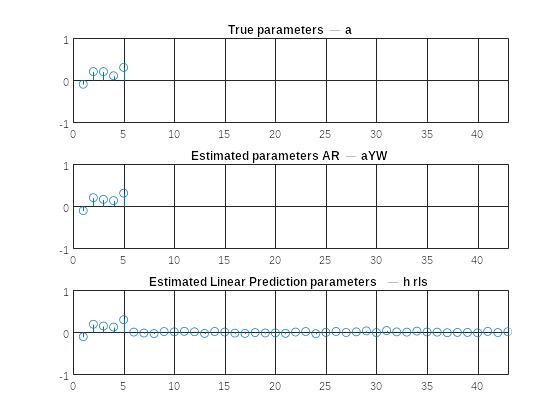
Рис. 13 Графики вектора заданных параметров АР-МОДЕЛИ, их оценок и вектора оценок параметров линейного предсказания

Значения MAE_AR = 0.016154 MAE_LP = 0.016154

Пояснения:

Рис.18. Структурная схема оценки параметров линейного предсказания сигнала.

Задача линейного предсказания заключается в определении параметров линейного предсказания ak , k=1, 2, ... , (M-1) , обеспечивающих наилучшее приближение оценки текущего отсчета к его истинному значению x(n) по заданному критерию, в качестве которого выбирается минимум среднего квадрата ошибки линейного предсказания ε(n).

Параметры АФ становятся оценками параметров линейного предсказания при (hi – параметры АФ, ak – параметры линейного предсказания):

Сравнение полученных оценок по критерию средней абсолютной ошибки – MAE – на одинаковой длине N КИХ-фильтра в составе АФ:

Для АР-модели с дополнением N-(M-1) нулями до длины N.

РАБОТА ЗАВЕРШЕНА