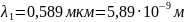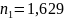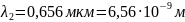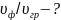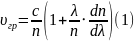КонтрольнаяВариант9
.docxМинистерство образования и науки Российской Федерации
Государственное образовательное бюджетное учреждение
высшего образования
«ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
(ВолгГТУ)
Кафедра «Физика»
Контрольная работа №2
по физике
Вариант №9
Выполнил:
Sol Invictus
Проверил:
Доцент
Краткая рецензия://Работа под заказ, ошибок быть не может ……………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………
Оценка работы _________________ баллов
Волгоград 202*
1. На концах никелинового проводника длиной 5 м поддерживается разность потенциалов 12 В. Определить плотность тока в проводнике, если его температура 540°С.
Дано: |
Решение: |
t = 540°С |
По
закону Ома, в дифференциальной форме
плотность тока j
в проводнике пропорциональна
напряженности Е
поля в
проводнике
где
С другой стороны,
где U — напряжение на концах проводника длиной l. Тогда
|
Найти:
|
ρ0 = 0,42 · 10-6 Ом · м - удельное сопротивление никелина при t = 0 °С,
α = 0,1 · 10-3 К-1 - температурный коэффициент сопротивления.
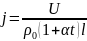
Вычисления:

Ответ:
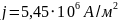
2. Определить ЭДС аккумуляторной батареи, ток короткого замыкания которой 10 А, если при подключении к ней резистора сопротивлением 9 Ом сила тока в цепи рвана 1 А.
Дано: |
Решение: |
Iкз = 10 A R = 9 Ом I = 1 А. |
Сила тока, по закону Ома для замкнутой цепи:
ℇ - ЭДС, r - внутреннее сопротивление источника тока.
|
Найти:
|


При коротком замыкании цепи внешнее сопротивление R = 0 и
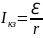
откуда

Подставим в ЭДС


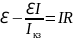

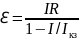
Вычисления:
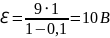
Ответ: ℇ = 10 В
3. При включении электромотора в сеть с напряжением U = 220 В он потребляет ток I = 5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление R обмотки мотора равно 6 Ом.
Дано: |
Решение: |
U = 220 В I = 5 А. R = 6 Ом
Найти: P- ? = ? |
Потребляемая мощность
Мощность, которая выделяется на обмотке
|
Полезная мощность
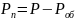
КПД
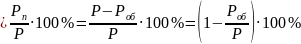
Вычисления:

Ответ:
4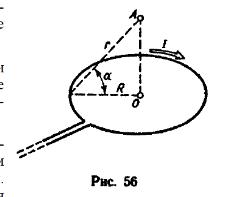 .
По
тонкому кольцу течет ток I
=
80 А.
Определить магнитную индукцию В
в
точке А,
равноудаленной
от точек кольца на расстояние r
=
10 см
(рис. 56). Угол α
=
π/6.
.
По
тонкому кольцу течет ток I
=
80 А.
Определить магнитную индукцию В
в
точке А,
равноудаленной
от точек кольца на расстояние r
=
10 см
(рис. 56). Угол α
=
π/6.
Дано: |
Решение: |
I = 80 А r = 10 см = 0,1 м α = π/6 |
Выделим на кольце
элемент dl
и от него в точку А
проведем радиус-вектор
где
|
Найти:
В
|
По
правилу правого винта определяем
направления векторов напряженности
 и
и
 магнитных полей, созданных в точке О
элементами тока
,
лежащими на одном диаметре кольца.
магнитных полей, созданных в точке О
элементами тока
,
лежащими на одном диаметре кольца.

Спроецируем
и
на оси х
и у.
 ,
следовательно,
угол
=∠САО,
так как углы со взаимно перпендикулярными
сторонами.
,
следовательно,
угол
=∠САО,
так как углы со взаимно перпендикулярными
сторонами.
направлен под углом к оси y (рис.).
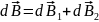 (для
двух диаметрально противоположных
элементов).
(для
двух диаметрально противоположных
элементов).
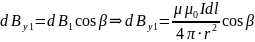

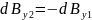
Сумма
проекций векторов
 на ось y будет равна
нулю.
на ось y будет равна
нулю.
Сумма проекций векторов на ось x:
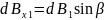
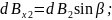
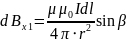
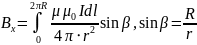
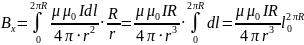
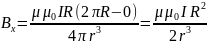
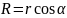

Подставим числа и проведем вычисления
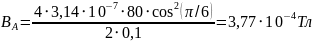
Ответ:
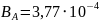 Тл
= 377 мкТл.
Тл
= 377 мкТл.
5. Протон прошел некоторую ускоряющую разность потенциалов U и влетел в скрещенные под прямым углом однородные поля: магнитное (В = 5 мТл) и электрическое (Е = 20 кВ/м). Определить разность потенциалов U, если протон в скрещенных полях движется прямолинейно.
Дано: |
Решение: |
Е
= 20 кВ/м = 2
|
Протон
влетел в электрическое и магнитное
поля. Со стороны электрического поля
на него действует электрическая сила
|
Найти:
|
В
электрическом поле направление силы
для положительно заряженной частицы
будет совпадать с направлением поля
 .
.
двигаясь перпендикулярно обоим полям, протон не будет испытывать отклонений от прямолинейной траектории, если силы, действующие на нее, будут скомпенсированы, т.е.:
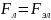
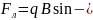 сила
Лоренца, действует со стороны магнитного
поля.
сила
Лоренца, действует со стороны магнитного
поля.
 сила,
действующая со стороны электрического
поля.
сила,
действующая со стороны электрического
поля.
где
- угол между вектором магнитной индукции
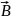 и вектором скорости
и вектором скорости
 .
.
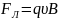


Скорость
частицы:
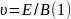 .
.
Пройдя ускоряющую разность потенциалов протон приобретет кинетическую энергию:

Работа
сил поля будет равна

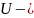 разность
потенциалов,
разность
потенциалов,
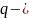 заряд. По закону сохранения энергии:
заряд. По закону сохранения энергии:

Заменим скорость (1) и найдем разность потенциалов
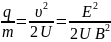
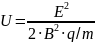
– удельный заряд протона.
Вычисления:
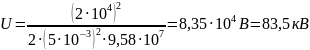
Ответ:

6. Прямой проводящий стержень длиной ℓ = 40 см находится в однородном магнитном поле (В = 0,1 Тл). Концы стержня замкнуты гибким проводом, находящимся вне поля. Сопротивление всей цепи R = 0,5 Ом. Какая мощность Р потребуется для равномерного перемещения стержня перпендикулярно линиям магнитной индукции со скоростью v = 10 м/с?
Дано: |
Решение: |
ℓ = 40 см = 0,4 м В = 0,1 Тл
R = 0,5 Ом
Найти: Р - ? |
При движении проводник будет пересекать линии индукции. За счёт этого в проводнике возникнет ЭДС индукции. ЭДС, возникающую в проводе, который движется в однородном магнитное поле, находят по формуле:
|
Ток, протекающий по проводнику, можно найти по закону Ома

Прохождение индукционного тока сопровождается выделением тепла.
Энергия, выделяемая в контуре, возникает за счет работы внешней силы.
Тепловая мощность, выделяемая на внешнем сопротивлении

Эта мощность будет равна мощности, которую необходимо подводить к системе за счёт внешней силы, действующей на проводник для того, чтобы скорость движения проводника была постоянной.
Вычисления:
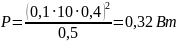
Ответ: 0,32 Вт
7. Установка для наблюдения колец Ньютона освещается монохроматическим светом, падающим нормально. Длина волны света 0,5 мкм. Найти радиус кривизны линзы, если диаметр пятого светлого кольца в проходящем свете равен 10 мм.
Дано: |
Решение: |
n = 1 |
Кольца
Ньютона возникают, если направить
свет на линзу, которая выпуклой стороной
соприкасается с плоской поверхностью
хорошо отполированной пластинки. При
этом образуется воздушная
прослойка
между
поверхностями линзы и пластинки,
толщина которой
|
Найти:
|
Рисунок

При
нормальном падении оптическая разность
хода между этими лучами равна удвоенной
толщине воздушного зазора –
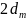 .
.
Оптическая
разность хода –
произведение
геометрической разности хода волн на
показатель преломления среды -
 .
.
Так как при отражении от границы жидкость-стекло фаза меняется на π (потеря полуволны), происходит дважды, и оптическая разность хода Δ равна:
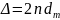 ,
,
где n – показатель преломления воздуха.
Для
того чтобы кольцо было светлым необходимо,
чтобы Δ=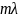 :
:

Откуда толщина воздушного зазора:

Радиус
rm
m-го кольца определяется из треугольника
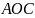 :
:
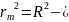
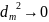 , поэтому
, поэтому

Откуда
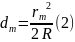
Приравняем (1) и (2) и выразим 𝑅:
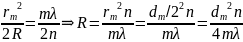
Вычисления:
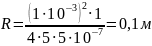
Ответ: 𝑅 = 0,1 м
8. На грань кристалла каменной соли падает узкий пучок рентгеновских лучей (λ = 0,15 нм). Под каким углом к поверхности кристалла должны падать лучи, чтобы наблюдался дифракционный максимум первого порядка? Расстояние между атомными плоскостями кристалла равно 0,285 нм.
Дано |
Решение: |
|
|
Найти:
|
Разность
хода двух волн, которые отражаются от
соседних атомных слоев, равна:
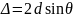 .
.
Согласно
теории Брэгга – Вульфа, максимумы
возникают при отражении рентгеновских
лучей от системы параллельных
кристаллографических плоскостей, когда
лучи, отражённые разными плоскостями
этой системы, имеют разность хода, равную
целому числу длин волн: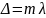 ,
где
- постоянная кристаллической решетки,
,
где
- постоянная кристаллической решетки,
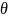 - угол скользящего падения, n - порядок
дифракционного максимума.
- угол скользящего падения, n - порядок
дифракционного максимума.
Приравняем
 и выразим 𝜗:
и выразим 𝜗:
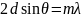 - уравнение Вульфа – Брэгга.
- уравнение Вульфа – Брэгга.
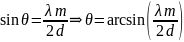
Вычисления
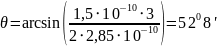
Ответ:

9. Кварцевую пластинку толщиной 3 мм, вырезанную перпендикулярно оптической оси, поместили между двумя поляризаторами. Определить постоянную вращения кварца для красного света, если его интенсивность после прохождения этой системы максимальна, когда угол между главными плоскостями поляризаторов 45°.
Дано: |
Решение: |
d=3 мм
|
При
прохождении через оптически активное
вещество в твердых телах угол поворота
плоскости поляризации
монохроматического света:
|
Найти:
|
Максимальная интенсивность прошедшего через систему из двух поляризаторов получается, если оптические оси поляризатора и анализатора параллельны.
По условию задачи интенсивность после прохождения системы из поляризаторов и пластины максимальна, когда угол между главными плоскостями поляризаторов равен .
Для того чтобы свет полностью проходил необходимо повернуть плоскость поляризации света на угол , так как изначально поляризаторы скрещены. Поэтому


Вычисления:
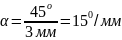
Ответ.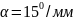
10. Найти отношение фазовой скорости к групповой для света с длиной волны 0,589 мкм в сероуглероде, если известно, что показатель преломления для этой длины волны равен 1,629, а для волны длиной 0,656 мкм он равен 1,620.
Дано |
Решение |
Найти:
|
Зависимость групповой скорости u от показателя преломления n и длины волны имеет вид:
где с – скорость света в вакууме. |
Фазовая скорость определяется как
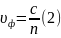


Средняя дисперсия:
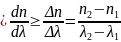
Для длины волны 1 и средней дисперсии имеем:

Вычисления:

Ответ:
 .
.

 м
м


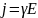 ,
,
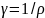 — удельная проводимость.
— удельная проводимость.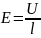
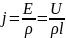

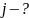
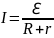
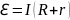
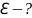
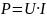
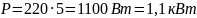


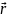 .
Магнитная индукция, создаваемая в
точке А
этим элементом тока, равна
.
Магнитная индукция, создаваемая в
точке А
этим элементом тока, равна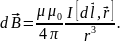
 - расстояние от кольца до точки; I –
сила тока;
- расстояние от кольца до точки; I –
сила тока;
 - магнитная проницаемость среды;
- магнитная проницаемость среды;
 Гн/м – магнитная постоянная,
Гн/м – магнитная постоянная,
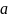 - расстояние от центра кольца. Так как
- расстояние от центра кольца. Так как
 перпендикулярно r.
перпендикулярно r.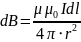
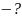

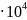 В/м
В/м =
9,58·107 Кл/кг
=
9,58·107 Кл/кг ,
со стороны магнитного поля – сила
Лоренца
,
со стороны магнитного поля – сила
Лоренца
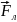 .
.


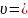 10
м/с
10
м/с
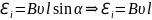
 индукция магнитного
поля
индукция магнитного
поля м
м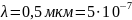 м
м
 постепенно
увеличивается от центра к краям.
постепенно
увеличивается от центра к краям.
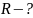
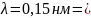

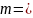 3
3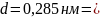




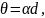 где
где
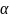 - постоянная вращения; d - длина пути,
пройденного светом в оптически активном
веществе.
- постоянная вращения; d - длина пути,
пройденного светом в оптически активном
веществе.