
КонтрольнаяВариант7
.docxМинистерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Волгоградский государственный технический университет»
Кировский вечерний факультет
Кафедра «Физика»
Контрольная работа |
по физике |
Вариант №7 |
Выполнил (а) |
|
Студент (ка) группы |
|
Ф.И.О. |
Sol invictus |
Проверил: |
доцент, к.ф.-м.н. |
|
(должность, степень, Ф.И.О.) |
Результат проверки: |
|
|
(оценка, дата, подпись преподавателя) |
Волгоград 202*
1.
Температура вольфрамовой нити электролампы
 ,
диаметр
,
диаметр
 ,
сила тока в ней
,
сила тока в ней
 .
Определить напряженность поля в нити.
.
Определить напряженность поля в нити.
Дано |
Решение |
|
По определению плотность тока равна:
где I – сила тока, S – поперечное сечение вольфрамовой нити. Площадь поперечного сечения вольфрамовой нити равна:
|
|
Запишем закон Ома в дифференциальной форме:
 ,
,
где
Е
– напряженность поля в нити,
 – удельное сопротивление.
– удельное сопротивление.

 – удельное
сопротивление вольфрама при температуре
– удельное
сопротивление вольфрама при температуре
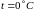 ,
,
 – температурный коэффициент сопротивления.
– температурный коэффициент сопротивления.
Из
уравнения
 имеем:
имеем:

Подставляем значения:

Проверка размерности:

Ответ:

2.
При каком внешнем сопротивлении
потребляемая полезная мощность будет
максимальной, если два одинаковых
источника тока с внутренним сопротивлением
 каждый
соединены параллельно?
каждый
соединены параллельно?
Дано |
Решение |
|
|
|
При параллельном соединении одинаковых источников тока батарея имеет такую же ЭДС, как и ЭДС одного элемента, т.е.

Внутреннее сопротивление батареи рассчитаем по правилу параллельного соединения сопротивлений:


Полезная мощность (мощность, выделяемая на внешнем участке цепи, сопротивление которого равно R) максимальна, если внутреннее сопротивление батареи r равно сопротивлению нагрузки R:

Подставляем значения:

Проверка размерности:

Ответ:

3.
Аккумулятор с ЭДС
 заряжается от сети постоянного тока с
напряжением
заряжается от сети постоянного тока с
напряжением
 .
Определить напряжение на клеммах
аккумулятора, если его внутреннее
сопротивление
.
Определить напряжение на клеммах
аккумулятора, если его внутреннее
сопротивление
 .
.
Дано |
Решение |
|
Составим эквивалентную схему:
|
|
Для расчета разветвленных цепей применим правило Кирхгофа. Выберем произвольное направление тока, как оно показано на рисунке, и условимся обходить контур по направлению тока (оно изображено внутри контура полукругом).
По второму закону Кирхгофа для контура запишем:

Откуда ток в цепи равен:
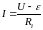
Тогда
напряжение на сопротивлении
 равно:
равно:

Подставляем числа:

Проверка размерности:

Ответ:

4.
По двум бесконечно длинным проводам,
скрещенным под прямым углом, текут токи
 и
и
 (
(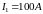 ).
Определить магнитную индукцию В
в
точке
А,
равноудаленной
от проводов на расстояние
).
Определить магнитную индукцию В
в
точке
А,
равноудаленной
от проводов на расстояние
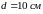 .
.
Дано |
Решение |
|
|
|
Бесконечно длинный проводник с током создает в точке А магнитное поле в индукцией:

Бесконечно
длинный проводник с током
 создает
в точке А
магнитное поле в индукцией:
создает
в точке А
магнитное поле в индукцией:

Магнитную индукцию найдем исходя из принципа суперпозиции полей:
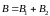
Так как вектора
 ,
то суммарный вектор индукции найдем по
теореме Пифагора:
,
то суммарный вектор индукции найдем по
теореме Пифагора:

По условию , тогда получаем:

Подставляем числа:

Проверка размерности:

Ответ:

5.
Однозарядные ион лития массой
 прошел ускоряющую разность потенциалов
прошел ускоряющую разность потенциалов
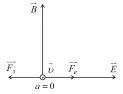
 и влетел в скрещенные под прямым углом
однородные магнитное и электрическое
поля. Определить магнитную индукцию В
поля,
если траектория иона в скрещенных полях
прямолинейна. Напряженность Е
электрического
поля равна
и влетел в скрещенные под прямым углом
однородные магнитное и электрическое
поля. Определить магнитную индукцию В
поля,
если траектория иона в скрещенных полях
прямолинейна. Напряженность Е
электрического
поля равна
 .
.
Дано |
Решение |
|
|
|
Кинетическая
энергия иона лития, прошедшего разность
потенциалов
 ,
согласно закону сохранения энергии
равна:
,
согласно закону сохранения энергии
равна:
 ,
,
отсюда скорость иона:
 .
.
На ион лития, движущийся перпендикулярно магнитному полю, действует сила Лоренца

где B – индукция магнитного поля.
Так как
 ,
то
,
то
 ,
получаем:
,
получаем:

Со стороны электрического поля тоже действует сила равная
 .
.
Результирующая сила равна сумме этих векторов:

Угол между векторами
 и
и
 равен
равен
 .
.
Модуль силы тогда равен:

Так как ион лития
двигается
прямолинейно, то действие сил должно
быть скомпенсированным. Иначе
перпендикулярно вектору скорости будет
действовать сила, которая будет искривлять
траекторию иона. Поэтому
 .
.
То есть
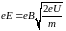 ,
,
 ,
,

Подставляем числа:

Проверка размерности:

Ответ:

6.
Проволочный виток диаметром
 и сопротивлением
и сопротивлением
 находится
в однородном магнитном поле (
находится
в однородном магнитном поле (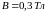 ).
Плоскость витка составляет угол
).
Плоскость витка составляет угол
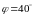 с линиями индукции. Какой заряд
с линиями индукции. Какой заряд
 протечет
по витку при выключении магнитного
поля?
протечет
по витку при выключении магнитного
поля?
Дано |
Решение |
|
|
|
Площадь кругового витка диаметром D равна:

Если магнитное поле однородное с индукцией В, то площадь витка будет пронизывать магнитный поток:
 ,
,
где
 – угол между нормалью
– угол между нормалью
 к плоскости витка и вектором
к плоскости витка и вектором
 ,
,
 – угол между
плоскостью витка и вектором
.
– угол между
плоскостью витка и вектором
.
После выключения магнитного поля магнитный поток равен:
 .
.
По закону Фарадея ЭДС индукции равно отношению изменения магнитного потока ко времени:
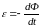
С другой стороны, по закону Ома:

Тогда

Ток
за время
 пронесет по контуру заряд:
пронесет по контуру заряд:

За все время изменения поля по контуру пройдет заряд



Подставляем числа:

Проверка размерности:

Ответ:
 .
.
7.
На тонкий стеклянный клин падает
нормально монохроматический свет.
Наименьшая толщина клина, с которой
видны интерференционные полосы в
отраженном свете, равна
 .
Расстояние между полосами
.
Расстояние между полосами
 .
Найти угол между поверхностями клина.
.
Найти угол между поверхностями клина.
Дано |
Решение |
|
|
|
Первый интерференционный максимум образован в том месте, где толщина клина равна d. С учетом того, что один луч отражается от оптически более плотной среды, разность хода лучей в этом месте равна наименьшему нечетному числу (1∙λ/2) длин полуволн:

где n – показатель преломления стекла.
Откуда длина световой волны

Разность хода лучей для второго максимума на λ больше, чем для первого:


Из подобия треугольников следует:
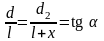
Исключим l:
 ,
,
 ,
,
 ,
,


Подставляем числа:
 (
( )
)
Ответ:
 град.
град.
8.
Чему должна быть равна ширина дифракционной
решетки с периодом
 ,
чтобы в спектре первого порядка был
разрешен дублет
,
чтобы в спектре первого порядка был
разрешен дублет
 и
и
 ?
?
Дано |
Решение |
|
Пусть есть две
спектральные линии с близкими длинами
волн
|
|
Разрешающая
способность
 дифракционной решетки равна:
дифракционной решетки равна:
 .
.
С другой стороны,
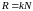 ,
,
где
 – порядок спектра,
– порядок спектра,
 – число штрихов дифракционной решетки.
– число штрихов дифракционной решетки.
Таким образом, две линии будут разрешены, если выполняется условие:
 .
.
Число
штрихов дифракционной решетки равно:

Тогда

Подставляем числа:
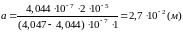
Проверка размерности:

Ответ:
 9.
Чему равен угол между главными плоскостями
двух поляризаторов, если интенсивность
естественного света, прошедшего через
них, уменьшилась в 5,4
раза? Считать, что каждый поляризатор
отражает и поглощает 14%
падающего на них света.
9.
Чему равен угол между главными плоскостями
двух поляризаторов, если интенсивность
естественного света, прошедшего через
них, уменьшилась в 5,4
раза? Считать, что каждый поляризатор
отражает и поглощает 14%
падающего на них света.
Дано |
Решение |
|
Пусть интенсивность
света на входе первого поляризатора
равна
Если на первый поляризатор падает естественный свет, то интенсивность вышедшего из поляризатора света равна половине без учета рассеивания:
|
|
С учетом рассеяния:
 .
.
Тогда интенсивность света после анализатора (второго поляризатора) равна:

Зная уменьшение интенсивности света при прохождении поляризатора и анализатора, находим угол между плоскостями поляризатора и анализатора:

Подставляем числа:

Ответ:

10.
Найти отношение групповой скорости к
фазовой для света с длиной волны
 в среде с показателем преломления
в среде с показателем преломления
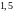 и дисперсией
и дисперсией
 .
.
Дано |
Решение |
|
Групповая скорость определяется выражением:
где с – скорость распространения света в вакууме. |
|
Фазовая скорость равна:
 .
.
Тогда отношение групповой скорости к фазовой
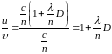
Подставляем числа:

Проверка размерности:

Ответ:
 .
.


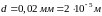



 ,
, .
.













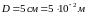










 и
и
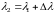 .
Они будут считаться разрешенными,
если главный максимум дифракционной
картины для одной длины волны совпадает
с первым дифракционным минимумом того
же порядка для второй длины волны.
.
Они будут считаться разрешенными,
если главный максимум дифракционной
картины для одной длины волны совпадает
с первым дифракционным минимумом того
же порядка для второй длины волны.



 .
.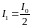



 ,
,