КонтрольнаяВариант4

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Волгоградский государственный технический университет»

Кировский вечерний факультет

Кафедра «Физика»

Контрольная работа

по физике

Вариант № 4

Выполнил (а)
Студент (ка) группы
Ф.И.О.	Sol Invictus
Проверил:	доцент, к.ф.-м.н..
	(должность, степень, Ф.И.О.)
Результат проверки:
	(оценка, дата, подпись преподавателя)

Волгоград 202*

Вариант 4

Задача 1

Определить заряд, прошедший по резистору за 10 с, если сила тока в резисторе за это время равномерно возрастала от 0 до 5 А.

Дано:

t = 10 с

I₁ = 0

I₂ = 5 А

Q - ?

Решение:

По закону Джоуля-Ленца

I = dQ/dt

Тогда заряд за время t:

Q =

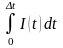
Зависимость I(t) – линейная: I(t) = kt + b

Из условия I(0) = I₁ = 0, находим b = 0. Из условия I(t) = I₂, находим k = I₂/t,

I(t) = I₂t/t,

Q =

Подставляя численные значения, находим:

Q = 510/2 = 25 Кл.

Ответ: Q = 25 Кл.

Задача 2

КПД аккумуляторной батареи при силе тока 2 А равен 0,8. Определить внутреннее сопротивление батареи, если ее ЭДС равна 10 В.

Дано:

I = 2 А

 = 0,8

 = 10 В

r - ?

Решение:

По определению КПД источника тока

 = ( - Ir)/

Тогда внутреннее сопротивление батареи

r = (1 - )/I

Подставляя численные значения, находим:

r = (1 – 0,8)10/2 = 1 Ом.

Ответ: r = 1 Ом.

Задача 3

От батареи, ЭДС которой  = 600 В, требуется передать энергию на расстояние 1 = 1 км. Потребляемая мощность Р = 5 кВт. Найти минимальные потери мощности в сети, если диаметр медных подводящих проводов d = 0,5 см.

Дано:

 = 600 В

1 = 1 км = 1000 м

Р = 5 кВт = 5000 Вт

d = 0,5 см = 0,005 м

 - ?

Решение:

Относительная потеря мощности в проводах вычисляется по формуле:

 = ,

где I²R – мощность теряемая в проводах, Р – мощность на нагрузке. Сопротивление проводов

R = 2l/S,

 = 1710^-9 Омм – удельное сопротивление меди, S = ¼d² – площадь сечения проводов.

По закону Ома для полной цепи

 = I(R + R_н) = IR + P/I

I = I²R + P

I²R - I + P = 0

I =

 =

 =

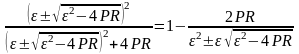
Меньшее значение :

 =

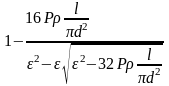
Подставляя численные значения, находим:

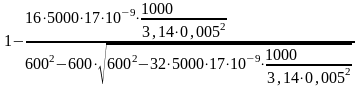 = = 0,025 = 2,5%.

Ответ:  = 2,5%.

Задача 4

По двум скрещенным под прямым углом бесконечно длинным проводам текут токи I и 2I (I = 100 А). Определить магнитную индукцию B в точке A. Расстояние d = 10 см.

Д ано: В₁

I₁ = I

I₂ = 2I

I = 100 А

d = 10 см = 0,1 м

В - ?

Решение:

Вектор магнитной индукции поля В₁, создаваемого проводником с током I в точке А направлен вверх, модуль его равен

В₁ = ₀I₁/(2d) = ₀I/(2d)

Вектор магнитной индукции поля В₂, создаваемого проводником с током 2I в точке А направлен перпендикулярно плоскости чертежа, от нас, модуль его равен

В₂ = ₀I₂/(22d) = ₀I/(2d)

По принципу суперпозиции

В = В₁ + В₂

Векторы взаимно перпендикулярны, результирующий вектор найдем по теореме Пифагора:

В =

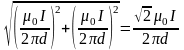
Подставляя численные значения, находим:

В = 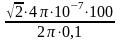= 28310^-6 Тл = 283 мкТл.

Ответ: В = 283 мкТл.

Задача 5

Альфа-частица влетела в скрещенные под прямым углом магнитное (B = 5 мТл) и электрическое (Е = 30 кВ/м) поля. Определить ускорение а альфа-частицы (Ускорение определяется в момент вхождения заряженной частицы в область пространства, где локализованы однородные магнитное и электрическое поля), если ее скорость v (v = 210⁶ м/c) перпендикулярна векторам В и Е, причём силы, действующие со стороны этих полей, противонаправлены.

Дано:

B = 5 мТл = 510^-3 Тл

Е = 30 кВ/м = 3010³ В/м

v = 210⁶ м/c

а - ?

Решение:

На частицу, движущуюся перпендикулярно магнитному полю, действует сила Лоренца

F_Л = qvB.

Со стороны электрического поля тоже действует сила равная

F_e = qE.

Результирующая сила по принципу суперпозиции

F = F_e – F_Л

F = qE – vB

Из второго закона Ньютона ускорение частицы

а = F/m = qE – vB/m

Заряд -частицы q = 2е, масса m = 4m_p, где е – заряд электрона, m_р – масса протона. Тогда

а = еE – vB/(2m_р)

Подставляя численные значения, находим:

а = 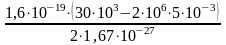= 9,610¹¹ м/с.

Ответ: а = 9,610¹¹ м/с.

Задача 6

В проволочное кольцо, присоединенное к баллистическому гальванометру, вставили прямой магнит. При этом по цепи прошел заряд Q = 50мкКл. Определить изменение магнитного потока Ф через кольцо; если сопротивление цепи гальванометра R = 10 Ом. Дано:

Q = 50мкКл = 5010^-6 Кл

R = 10 Ом

Ф - ?

Решение:

По закону Фарадея ЭДС равна отношению изменения магнитного потока к времени

 = -Ф/t.

Откуда

Ф = t

По закону Ома

 = IR = QR/t

Ф = QR

Подставляя численные значения, находим:

Ф = 5010^-610 = 0,510^-3 Вб = 0,5 мВб.

Ответ: Ф = 0,5 мВб.

Задача 7

На пленку из глицерина толщиной 0,3 мкм падает белый свет. Каким будет казаться цвет пленки в отраженном свете, если угол падения лучей 45°? Дано:

n = 1,47

d = 0,3 мкм = 0,310^-6 м

i = 45

 - ?

Решение:

Условие максимума при интерференции

 = k.

Разность хода лучей  при интерференции на тонкой пленке толщиной d:

 =

= k

Полагая k = 1, получим

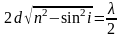
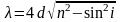
Подставляя численные значения, находим:

= 1,5510^-6 м = 1,55 мкм.

Такая длина волны соответствует инфракрасной части спектра, свет не будет видимым.

Ответ:  = 1,55 мкм.

Задача 8

На узкую щель нормально падает плоская монохроматическая световая волна ( = 628 нм). Чему равна ширина щели, если второй дифракционный максимум наблюдается под углом 1°30? Дано:

 = 628 нм = 62810^-9 м

m = 2

 = 1°30 b - ?

Решение:

Для дифракции Фраунгофера на щели формула распределения интенсивности света по направлениям

I = I₀(sin/),

где

 = bsin/

Функция I имеет максимумы при  = 0 и  = (2m + 1)/2, поэтому максимумы наблюдаются при

sin = (2m + 1)/(2b)

Откуд

b = (2m + 1)/(2 sin)

Подставляя численные значения, находим:

b = 562810^-9/(2sin1,5) = 6010^-6 м = 60 мкм.

Ответ: b = 60 мкм.

Задача 9

Естественный свет падает на поверхность диэлектрика пол углом полной поляризации. Коэффициент пропускания света равен 0,915. Найти степень поляризация преломленного луча. Дано:

 = 0,915

Р - ?

Решение:

Степень поляризация преломленного луча

Р = I/I,

где I - интенсивность отраженного света; I - интенсивность преломленной волны.

Коэффициент пропускания света

 = I/I = I/(I + I)

1/ = I/I + 1 = P + 1

P = 1/ - 1

P = 1/0,915 – 1 = 0,093.

Ответ: Р = 0,093.

Задача 10

Определить относительное отклонение групповой скорости от фазовой для света с длиной волны 0,6 мкм в среде с показателем преломления 1,6 и дисперсией – 410⁴ м^-1. Дано:

 = 0,6 мкм = 0,610^-6 м

n = 1,6

D = -410⁴ м^-1

 - ?

Решение:

Групповая скорость определяется как

u =

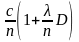
Фазовая скорость

 = с/n

Относительное отклонение групповой скорости от фазовой

 = ( - u)/ =

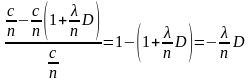
Подставляя численные значения, находим:

 = 0,610^-6410⁴/1,6 = 1,510^-2;

 = 1,5 %.

Ответ:  = 1,5 %.