
курсовая работа / полиномы лагранжа
.docxМедведев Г.Н. гр.9587
Функция: x=2*cos(2*t)+2*sin(sqrt(2)*t), t [27pi;28pi]
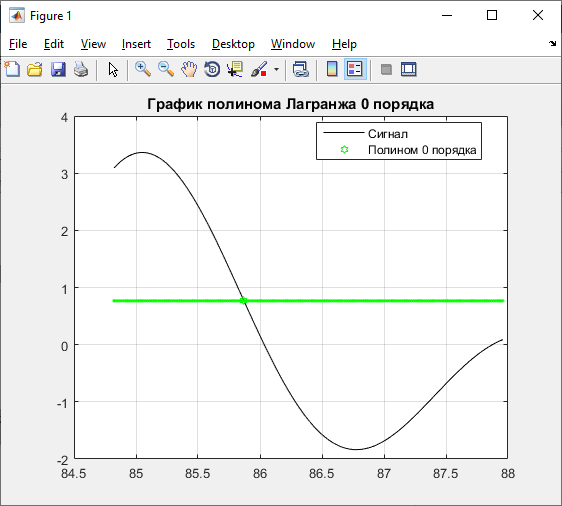
Полином Лагранжа 0 порядка:
Tn=27*pi;
deltaT=0.015;
Tv=28*pi;
t=Tn:deltaT:Tv;
x=2*cos(2*t)+2*sin(sqrt(2)*t);
figure(1);
plot(t,x,'k');
hold on;
grid on;
t0=Tn;
dt=pi/3;
f1=2*cos(2*(dt+27*pi))+2*sin(sqrt(2)*(dt+27*pi));
plot((27*pi+dt),f1,'gh');
t1=27*pi+pi/2;
p=f1;
plot(t,p,'g.');
hold on;
title ('График полинома Лагранжа 0 порядка');
legend ('Сигнал','Полином 0 порядка','Location','Best');
hold on;
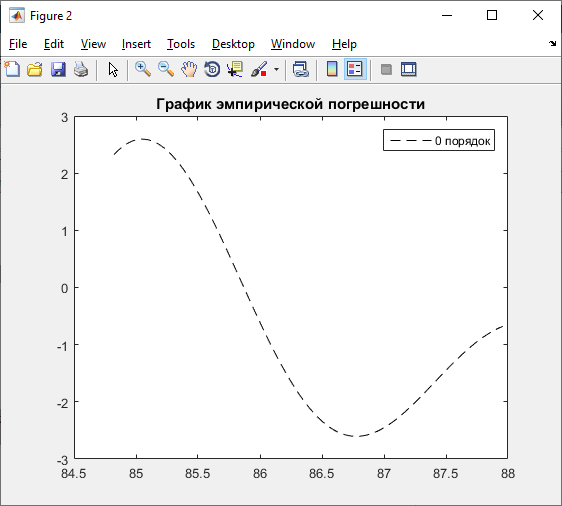
ep1=x-p;%эмпирическая погрешность
figure(2);
plot(t, ep1, 'k--');
title ('График эмпирической погрешности');
legend('0 порядок');
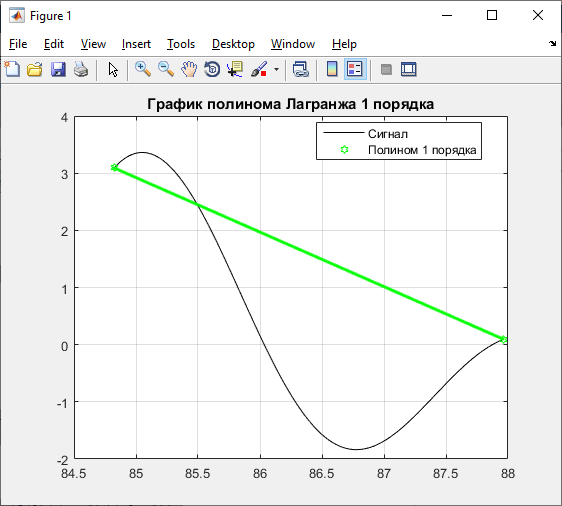
Полином Лагранжа 1 порядка:
Tn=27*pi;
deltaT=0.015;
Tv=28*pi;
t=Tn:deltaT:Tv;
x=2*cos(2*t)+2*sin(sqrt(2)*t);
figure(1);
plot(t,x,'k');
hold on;
grid on;
t0=Tn;
dt=pi;
for j=1:1:2
f(j)=2*cos(2*(dt*(j-1)+27*pi))+2*sin(sqrt(2)*(dt*(j-1)+27*pi));
plot(27*pi+pi.*(j-1),f(j),'gh');
end
t1=27*pi;
t2=28*pi;
p=(f(1)*(t-t2)/(t1-t2))+(f(2)*(t-t1)/(t2-t1));
plot(t,p,'g.');
hold on;
title ('График полинома Лагранжа 1 порядка');
legend ('Сигнал','Полином 1 порядка','Location','Best');
hold on;
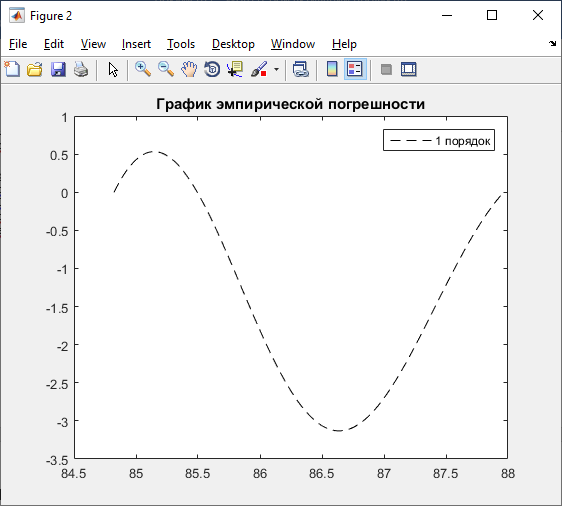
ep1=x-p;%эмпирическая погрешность
figure(2);
plot(t, ep1, 'k--');
title ('График эмпирической погрешности');
legend('1 порядок');
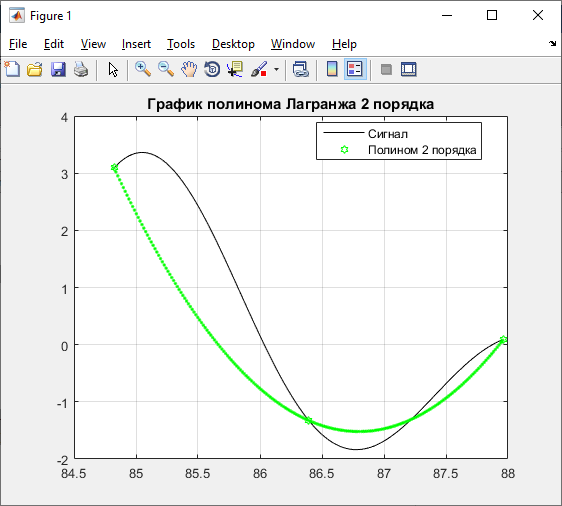
Полином Лагранжа 2 порядка:
Tn=27*pi;
deltaT=0.015;
Tv=28*pi;
t=Tn:deltaT:Tv;
x=2*cos(2*t)+2*sin(sqrt(2)*t);
figure(1);
plot(t,x,'k');
hold on;
grid on;
t0=Tn;
dt=pi/2;
for j=1:1:3
f(j)=2*cos(2*(dt*(j-1)+27*pi))+2*sin(sqrt(2)*(dt*(j-1)+27*pi));
plot(27*pi+pi.*(j-1)/2,f(j),'gh');
end
t1=27*pi;
t2=27*pi+pi/2;
t3=27*pi+2*pi/2;
p=(f(1)*(t-t2).*(t-t3))/((t1-t2).*(t1-t3))+(f(2)*(t-t1).*(t-t3))/((t2-t1).*(t2-t3))+(f(3)*(t-t1).*(t-t2))/((t3-t1).*(t3-t2));
plot(t,p,'g.');
hold on;
title ('График полинома Лагранжа 2 порядка');
legend ('Сигнал','Полином 2 порядка','Location','Best');
hold on;
ep2=x-p;%эмпирическая погрешность
figure(2);
plot(t, ep2, 'k--');
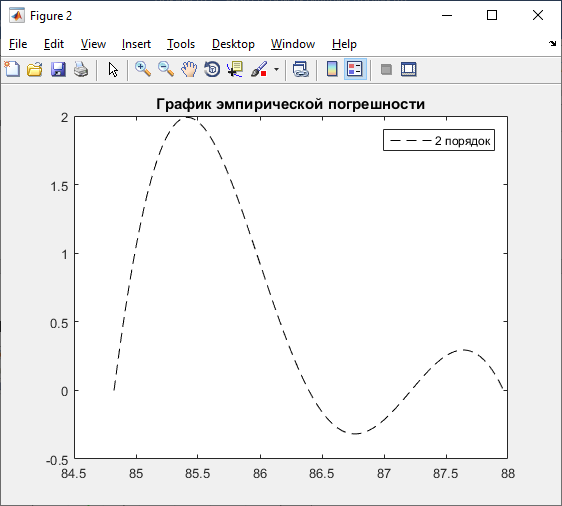
title ('График эмпирической погрешности');
legend('2 порядок');
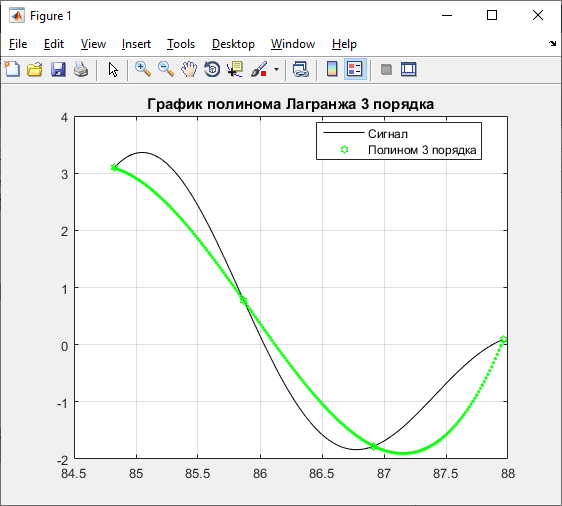
Полином Лагранжа 3 порядка:
Tn=27*pi;
deltaT=0.015;
Tv=28*pi;
t=Tn:deltaT:Tv;
x=2*cos(2*t)+2*sin(sqrt(2)*t);
figure(1);
plot(t,x,'k');
hold on;
grid on;
t0=Tn;
dt=pi/3;
for j=1:1:4
f(j)=2*cos(2*(dt*(j-1)+27*pi))+2*sin(sqrt(2)*(dt*(j-1)+27*pi));
plot(27*pi+pi.*(j-1)/3,f(j),'gh');
end
t1=27*pi;
t2=27*pi+pi/3;
t3=27*pi+2*pi/3;
t4=27*pi+3*pi/3;
p=(f(1)*(t-t2).*(t-t3).*(t-t4))/((t1-t2).*(t1-t3).*(t1-t4))+(f(2)*(t-t1).*(t-t3).*(t-t4))/((t2-t1).*(t2-t3).*(t2-t4))+(f(3)*(t-t1).*(t-t2).*(t-t4))/((t3-t1).*(t3-t2).*(t3-t4))+(f(4)*(t-t1).*(t-t2).*(t-t3))/((t4-t1).*(t4-t2).*(t4-t3));
plot(t,p,'g.');
hold on;
title ('График полинома Лагранжа 3 порядка');
legend ('Сигнал','Полином 3 порядка','Location','Best');
hold on;
ep3=x-p;%эмпирическая погрешность
figure(2);
plot(t, ep3, 'k--');
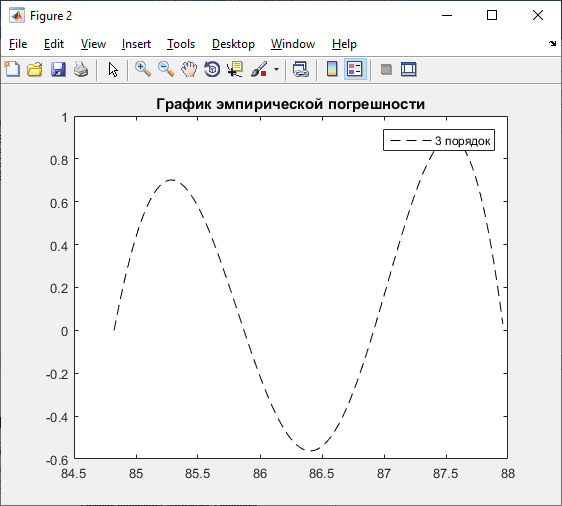
title ('График эмпирической погрешности');
legend('3 порядок');
Полином Лагранжа 4 порядка:
Tn=27*pi;
deltaT=0.015;
Tv=28*pi;
t=Tn:deltaT:Tv;
x=2*cos(2*t)+2*sin(sqrt(2)*t);
figure(1);
plot(t,x,'k');
hold on;
grid on;
t0=Tn;
dt=pi/4;
for j=1:1:5
f(j)=2*cos(2*(dt*(j-1)+27*pi))+2*sin(sqrt(2)*(dt*(j-1)+27*pi));
plot(27*pi+pi.*(j-1)/4,f(j),'gh');
end
t1=27*pi;
t2=27*pi+pi/4;
t3=27*pi+2*pi/4;
t4=27*pi+3*pi/4;
t5=27*pi+4*pi/4;
p=(f(1)*(t-t2).*(t-t3).*(t-t4).*(t-t5))/((t1-t2).*(t1-t3).*(t1-t4).*(t1-t5))+(f(2)*(t-t1).*(t-t3).*(t-t4).*(t-t5))/((t2-t1).*(t2-t3).*(t2-t4).*(t2-t5))+(f(3)*(t-t1).*(t-t2).*(t-t4).*(t-t5))/((t3-t1).*(t3-t2).*(t3-t4).*(t3-t5))+(f(4)*(t-t1).*(t-t2).*(t-t3).*(t-t5))/((t4-t1).*(t4-t2).*(t4-t3).*(t4-t5))+(f(5)*(t-t1).*(t-t2).*(t-t3).*(t-t4))/((t5-t1).*(t5-t2).*(t5-t3).*(t5-t4));
plot(t,p,'g.');
hold on;
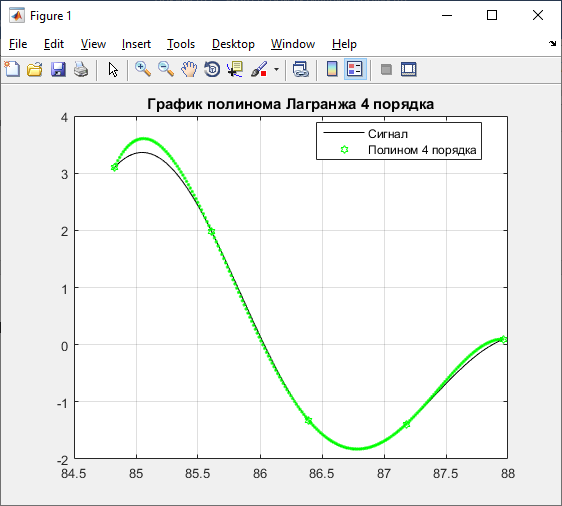
title ('График полинома Лагранжа 4 порядка');
legend ('Сигнал','Полином 4 порядка','Location','Best');
hold on;
ep3=x-p;%эмпирическая погрешность
figure(2);
plot(t, ep3, 'k--');
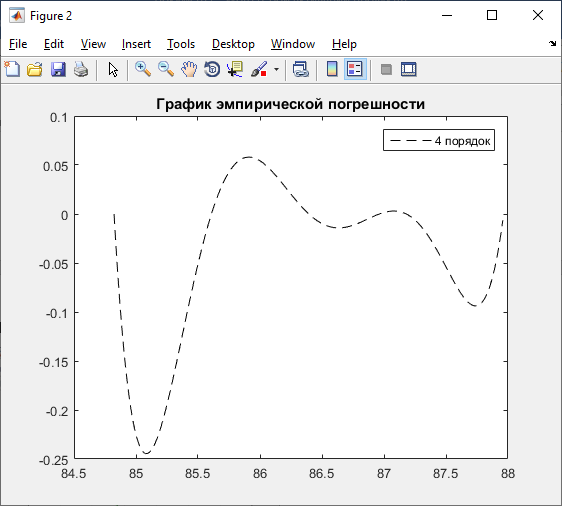
title ('График эмпирической погрешности');
legend('4 порядок');
